主成分分析PCA,最主要在数据处理中用来降维,比如说我们有1000组数据,每组数据有1000个样本,我们通过分析每组数据中的主要特征,剔除那些不必要的特征,使得数据的维度有所减少,以加快计算机计算的速度。进行PCA变化时主要有以下特征:
1、主成分不变;
2、有细微损失;
3、高维数据到低维数据。
进行PCA降维的主要步骤如下:
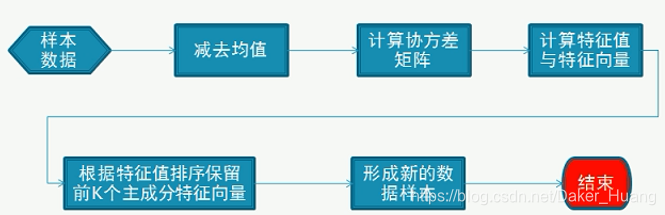
上图中的步骤比较抽象,其实就是经过一步步的矩阵运算得到最终的新的数据。具体公式如下:

实例代码:
#include<opencv2/opencv.hpp>
#include<iostream>
using namespace cv;
using namespace std;
double calcPCAorientation(Mat &image, vector<Point>pts);
int main(int argc, char** argv)
{
Mat src = imread("D:/test/pca_test1.jpg");
if (src.empty())
{
cout << "图片未找到..." << endl;
return -1;
}
imshow("input image", src);
Mat gray, binary;
//转为灰度图
cvtColor(src, gray, COLOR_BGR2GRAY);
//转为二值图
threshold(gray, binary, 0, 255, THRESH_BINARY | THRESH_OTSU);//自动获取阈值
imshow("binary image", binary);
vector<vector<Point>>contours;//存储轮廓点信息
vector<Vec4i>hierachy;
//轮廓发现
Mat result = src.clone();
findContours(binary, contours, hierachy, RETR_TREE, CHAIN_APPROX_SIMPLE,Point());
for (size_t t = 0; t < contours.size(); t++)
{
double area = contourArea(contours[t]);
if (area > 100000 || area < 100) //如果面积大于100000或小于100,则过滤掉该面积轮廓
continue;
drawContours(result, contours, t, Scalar(0, 0, 255), 2, 8);
double theta = calcPCAorientation(result, contours[t]);
}
imshow("contours image", result);
waitKey(0);
return 0;
}
double calcPCAorientation(Mat & image, vector<Point> pts)
{
int size = static_cast<int>(pts.size());//获取数据点个数
Mat data_pts = Mat(size, 2, CV_64FC1);//定义一个n行2列的矩阵
for (int i = 0; i < size; i++)
{
data_pts.at<double>(i, 0) = pts[i].x;//矩阵的第一列数据
data_pts.at<double>(i, 1) = pts[i].y;//矩阵的第二列数据
}
//PCA分析处理
PCA pca_analysis(data_pts, Mat(), PCA::DATA_AS_ROW);
Point cnt = Point(static_cast<int>(pca_analysis.mean.at<double>(0, 0)),//求均值,第一列一行
static_cast<int>(pca_analysis.mean.at<double>(0, 1)));//第一列第二行
circle(image, cnt, 2, Scalar(0, 255, 0), 2, 8, 0);
vector<Point2d>eigen_vectors(2);//2个特征向量
vector<double>eigen_vals(2);//2个特征值
for (int i = 0; i < 2; i++)
{
eigen_vals[i] = pca_analysis.eigenvalues.at<double>(i, 0);
eigen_vectors[i] = Point2d(pca_analysis.eigenvectors.at<double>(i, 0),
pca_analysis.eigenvectors.at<double>(i, 1));
cout << "第" << i << "个特征值为:" << eigen_vals[i] << endl;
}
Point p1 = cnt + 0.02*Point(static_cast<int>(eigen_vectors[0].x*eigen_vals[0]), static_cast<int>(eigen_vectors[0].y*eigen_vals[0]));
Point p2 = cnt - 0.05*Point(static_cast<int>(eigen_vectors[1].x*eigen_vals[1]), static_cast<int>(eigen_vectors[1].y*eigen_vals[1]));
double angle = atan2(eigen_vectors[0].y ,eigen_vectors[0].x); //反三角函数求角度
cout << "偏转角度=" << angle*(180/CV_PI) << endl;
cout << "-------------------------------" << endl;
cout << "-------------------------------" << endl;
line(image, cnt, p1, Scalar(255, 0, 0), 2, 8, 0);
line(image, cnt, p2, Scalar(255, 125, 0), 2, 8, 0);
/*
cout << "cnt=" << cnt << endl;
cout << "p1=" << p1 << endl;
cout << "p2=" << p2 << endl;
cout << "-----------------------" << endl;
*/
return 0;
}
运行结果:
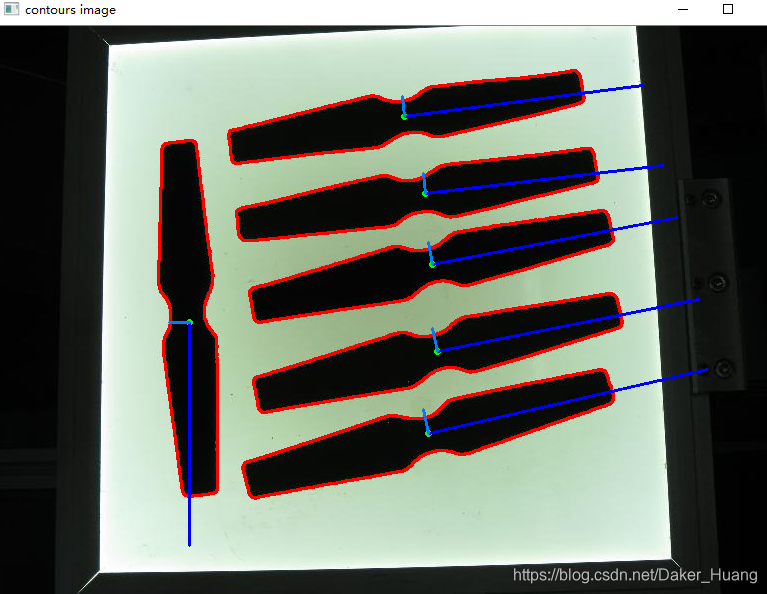
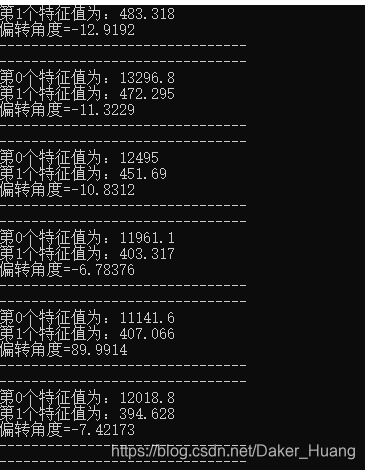








 本文深入探讨了主成分分析(PCA)在数据降维中的应用,通过实例代码展示了如何使用OpenCV库进行图像轮廓的PCA分析,提取主要特征并计算轮廓的偏转角度。
本文深入探讨了主成分分析(PCA)在数据降维中的应用,通过实例代码展示了如何使用OpenCV库进行图像轮廓的PCA分析,提取主要特征并计算轮廓的偏转角度。
















 1745
1745

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








