目录
0.写在前面
在前面我们已经学完了大部分C++中常用的语法,那么不妨让我们把C++运用到数据结构中,本篇要讲解的是二叉搜索树(Binary Search Tree),简称BST,如果你不知道这是什么?下面给出简要介绍:
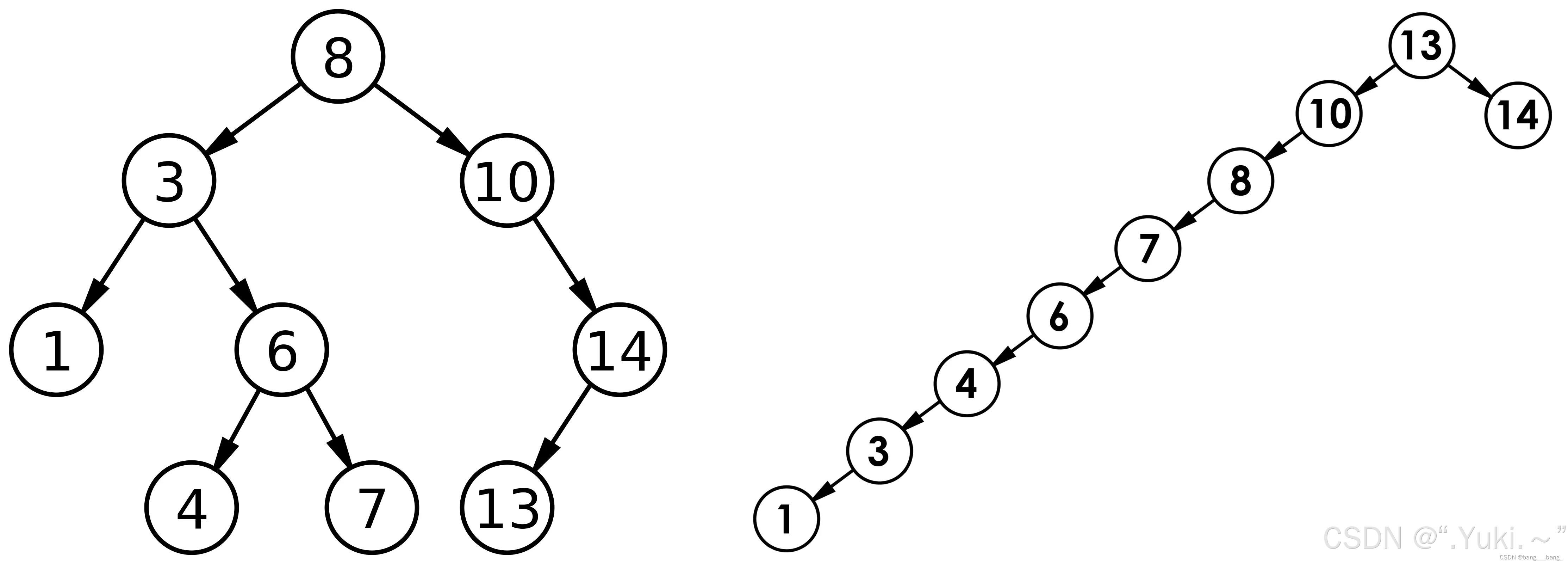
二叉搜索树(BST)是一种常用的数据结构,具有以下特点:
结构特性:
- 每个节点最多有两个子节点(左孩子和右孩子)
- 左子树中的所有节点值都小于父节点值
- 右子树中的所有节点值都大于父节点值
主要优势:
- 平均查找 / 插入 / 删除时间复杂度为 O (log n)
- 天然支持快速范围查询
- 中序遍历可得到有序序列
注意事项:
- 极端情况下可能退化为链表(O (n) 复杂度)
- 可通过平衡化改造(如 AVL 树、红黑树)优化性能,后续讲解
- 中序遍历是关键遍历方式,同时可以进行排序
1.运用非递归书写BST
1)BST结点的构造
思路:
---1--- 先来想想如何存储结点,如果我们使用堆那样的数组是否合适?当然不合适,因为涉及到下标访问的问题,那么还剩下链式结构可以供我们选择了。
---2--- 构造BinaryTreeNode当然是要方便类外直接进行访问的,因此用struct来构造,来想想一个结点要存储什么?
---3--- 在结点中存储left地址,right地址,以及当前结点的val,val可以是多种类型的,因此需要进行泛型编程,运用模板template
---4--- 最后要写一个构造函数,因为在创造结点的时候可能会用到,记得将left,right置为nullptr哦~
template<class T>
struct BinaryTreeNode
{
BinaryTreeNode* left;
BinaryTreeNode* right;
T val;
BinaryTreeNode(const T& t)
{
left = nullptr;
right = nullptr;
val = t;
}
};2)默认构造函数
思路:
---1--- 接下来要完成BST类的编写,我们还是在前面使用template,将BinaryTreeNode<T>重命名Node(这里<T>是对结点的实例化,属于一个类型,不是变量哦)方便后面少敲点字
---2--- 将成员变量设置为一个根节点_root就可以了,无需其他的成员变量,那么构造函数就很简单了,使用初始化列表将_root置为nullptr即可
BinarySearchTree()
:_root(nullptr)
{ }3)Insert插入函数
思路:
---1--- 将一个任意类型的t插入到BST中,这个函数的参数类型最好设置为const T& t,const可以防止权限的问题出现以及不期望被修改的值被篡改,设置引用则是提高传参效率,避免拷贝构造消耗时间内存
---2--- 用cur指针表示指针当前指向的位置,在cur不为nullptr的条件下去比较当前结点val与要插入t的值,因为BST左边的所有值比当前值小,右边所有值比当前值大,所以要去寻找能够插入t合适的位置,比当前值小就要去左子树寻找,相反较大就要去右子树寻找,直到cur为空,这时就找到了正确位置
---3--- 我们new一个新结点,前面结点中写的构造函数就派上用场了,将t传入构造,构造完成就要判断连接在上一结点的左边or右边
---4--- 这时才发现原来还要用一下前一个结点,看来要在前面加上prev指针,在cur每次往下寻找之前备份一下
---5--- 最后根据t的值与prev中的val比较,将结点连接到正确位置即可
---6--- 如果刚开始是空树,那么prev就是空,解引用会出现问题,做一下特殊处理~
bool Insert(const T& t)
{
Node* cur = _root;
Node* prev = nullptr;
while (cur)
{
if (t < cur->val)
{
prev = cur;
cur = cur->left;
}
else if (t > cur->val)
{
prev = cur;
cur = cur->right;
}
else
{
return false;
}
}
auto newnode = new Node(t);
//这里要对根结点为空特殊处理一下
if (_root == nullptr)
{
_root = newnode;
return true;
}
if (t < prev->val)
{
prev->left = newnode;
}
if (t > prev->val)
{
prev->right = newnode;
}
return true;
}4)InOrder中序遍历函数
思路:
---1--- 前面介绍过,对BST进行中序遍历,就相当于是在排序,中序遍历在二叉树章节详细介绍过
---2--- 这里不采用常规递归写法,我们使用栈来实现遍历,由于顺序是左子树->结点->右子树,所以只要左子树不为空,就将子树结点入栈
---3--- 在左子树为空后,将栈顶元素取出,这就是最后一个左子树的地址,将val尾插vector,pop这个子树结点,那么后面就可以对前一个左子树结点进行访问,最后将cur更新,继续入栈可能存在的新左子树
---4--- 当cur指向nullptr并且栈为空时就完成了遍历,打印vector
void InOrder()
{
vector<int> ret;
stack<TreeNode*> s;
TreeNode* cur = root;
while (cur || !s.empty())
{
while (cur)
{
s.push(cur);
cur = cur->left;
}
TreeNode* top = s.top();
ret.push_back(top->val);
s.pop();
cur = top->right;
}
for (auto e : ret)
{
cout << e << " ";
}
}5)find寻找函数
思路:
---1--- find函数实现去二叉搜索树中查找需要查找的数据,这里也比较好理解
---2--- 比较当前结点的值与查找值,小了就去左子树寻找,大了就去右子树寻找,与插入有相似之处
---3--- 寻找函数也是BST最基本最重要的功能函数,后面会进行扩展!
bool find(const T& t)
{
Node* cur = _root;
while (cur)
{
if (t < cur->val)
{
cur = cur->left;
}
else if (t > cur->val)
{
cur = cur->right;
}
else
{
return true;
}
}
return false;
}6)erase删除函数
思路:
Caution!这个函数最为复杂,做好准备~
---1--- 删除一个结点分为三种情况:
- 无子树
- 有左子树/右子树
- 左右子树都存在
对于前两种情况,可以用一种办法处理:右子树/左子树为空,那么就将左子树/右子树连接到父亲结点上,最后一种情况要用到替换法
---2--- 首先用cur找到要删除的val对应的结点的地址,判断是否属于第一/二种情况,如果是还要记录prev上一个结点,因为不知道这个要删除的结点位于上一个结点的左子树还是右子树
---3--- 替换法:对于左右子树都存在,那么就要去左子树寻找最大的值或者去右子树寻找最小的值,这里举例左子树寻大值leftMax
---4--- 寻找到最大值后,需要将leftMax的值与cur的val进行交换,将leftMax的左子树连接上一个结点,这时leftMax的右子树一定为nullptr,但是它不一定位于上一结点的right,如果要删除的结点的left为leftMax呢?所以这里还要一个parent结点用于判断(注意parent不能为nullptr,如果删除节点left就是leftMax,判断的时候就会对nullptr解引用,因为parent需要事先赋值cur
bool erase(const T& t)
{
//第一步先来找到含有t的结点
Node* cur = _root;
Node* prev = cur;//用于记录一下前一个结点,用于删除
//注意prev不能设置为nullptr,如果根节点就是要删除的值,prev就会对空指针解引用了
while (cur)
{
if (t > cur->val)
{
prev = cur;
cur = cur->right;
}
else if (t < cur->val)
{
prev = cur;
cur = cur->left;
}
else
{
//找到之后分为三种情况,度为0/1/2,
//这里将度为0/1统一处理为一种情况,直接将后面的结点接在prev上
if (cur->right == nullptr)
{
if (cur == _root)//对根结点进行删除,此时prev就是cur,不指向任意一边
{
_root = cur->left;
}
else
{
if (prev->right == cur)
{
prev->right = cur->left;
}
else
{
prev->left = cur->left;
}
}
}
else if (cur->left == nullptr)
{
if (cur == _root)
{
_root = cur->right;
}
else
{
if (prev->right == cur)
{
prev->right = cur->right;
}
else
{
prev->left = cur->right;
}
}
}
else
{
//第三种情况就复杂很多了,要找到左边所有元素最大的结点或者右边元素最小的节点
//这里书写左子树找最大结点,进行替换法
//关键点在于这里找到左边的最大一个结点,这个结点右边一定为空,不可能还有比这个还大的结点了
Node* parent = cur;//这里还是要注意不能为空,如果cur左边就是leftmax呢?就会对空指针解引用了
Node* leftMax = cur->left;//这里左节点一定存在!因为单个结点或者没有结点的情况上面已经讨论过了
while (leftMax->right)
{
parent = leftMax;
leftMax = leftMax->right;
}
swap(leftMax->val, cur->val);//交换两个值进行替换
//因为要对leftmax这个结点进行删除,那么一定要记录父亲结点
//这里leftmax就有可能在parent左边,也有可能在parent右边
if (parent->left == leftMax)
{
parent->left = leftMax->left;
}
else
{
parent->right = leftMax->left;
}
cur = leftMax;
}
delete cur;
return true;
}
}
return false;
}2.运用递归改良BST
1)InOrder中序遍历函数
思路:
---1--- 前面介绍过,对BST进行中序遍历,就相当于是在排序,中序遍历在二叉树章节详细介绍过
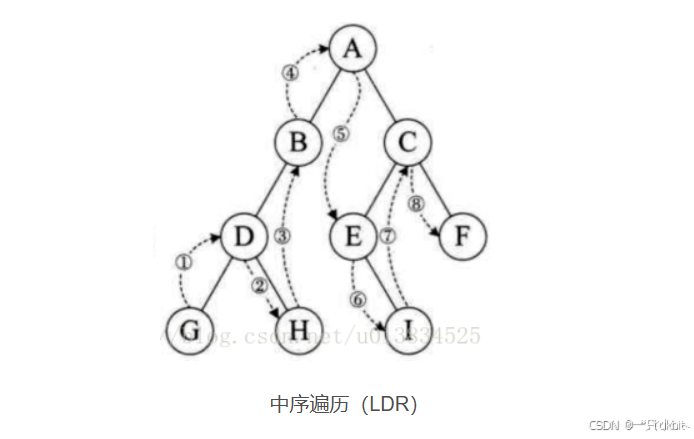
---2--- 这里运用双递归,顺序是左子树->结点->右子树,按照这个顺序最后设置递归出口,就完成了中序遍历
---3--- 如果对这一过程不太理解的同学,下面给出递归展开图
---4--- 注意这里不能直接递归,成员函数第一个参数都是this指针,所以我们需要额外编写一个子函数!
void InOrder()
{
_InOrder(_root);
}
void _InOrder(Node* root)
{
if (root == nullptr)
{
return;
}
_InOrder(root->left);
cout << root->val << " ";
_InOrder(root->right);
}2)insert函数
思路:
---1--- 这里使用递归写法,如果在传参时使用引用,就可以对实参进行修改,也无需对结点位于上一结点的left/right进行判断,大大简化
---2--- t>val就去右子树,相反则去左子树,如果==就返回false,BST当然不允许两个相同的值存在
---3--- 结点为nullptr直接对参数进行修改就行了,这里其实是为传参的地址取了别名,但从底层实现来看其实是二级指针,方便了使用
bool _Insert(Node*& root, const T& t)//非常巧妙的是,这里指针加了引用,可以对上一个指针进行修改,类似于二级指针,由于引用不可以改变指向,但递归是不停创建栈帧,因此不会改变只指向
{
if (root == nullptr)
{
Node* newnode = new Node(t);
root = newnode;
return true;
}
if (t > root->val)
{
return _Insert(root->right, t);
}
else if (t < root->val)
{
return _Insert(root->left, t);
}
else
{
return false;
}
}3)erase函数
思路:
---1--- 还是去寻找要删除的值,如果找到地址为nullptr的结点都没有找到就返回false
---2--- 大则去右,小则去左,找到了判断属于三种情况的哪一种
---3--- 前两种情况直接连接即可,对于第三种情况,还是去寻找leftMax,交换val,剩下就去cur的左子树删除这个t,构成递归即可
bool _erase(Node*& root, const T& t)
{
if (root == nullptr)
{
return false;
}
//这里也不需要记录父亲结点的地址了,引用非常的巧妙嗷!
if (t > root->val)
{
return _erase(root->right, t);
}
else if (t < root->val)
{
return _erase(root->left, t);
}
else
{
Node* del = root;//要删除的结点的地址还是要记录一下的
//还是分为三种情况,将度为0/1归为一种
//1.左为空
//2.右为空
//3.左右都不为空
if (root->left == nullptr)
{
root = root->right;
}
else if (root->right == nullptr)
{
root = root->left;
}
else
{
Node* leftMax = root->left;
while (leftMax->right)
{
leftMax = leftMax->right;
}
swap(leftMax->val, root->val);//替换法
return _erase(root->left, t);//直接去左边找要删除的这个数
//注意这里不可以找leftMax,因为如果直接对leftMax这个结点的指针区别名会出错,正确做法是对指向左边的指针取别名
}
delete del;
return true;
}4)析构函数
思路:
---1--- 析构函数采用后序遍历的思路实现,其特点是最后一个为根节点,这也符合析构的特点,最后释放根节点
---2--- 设置递归出口nullptr,先走左子树,再走右子树,最后调用erase函数删除当前结点的val
---3--- 注意在前面用析构函数去调用这里的Destroy子函数,才能实现递归!
void Destroy(Node*& root)
{
if (root == nullptr)
{
return;
}
//析构就要进行二叉树后序遍历
//左子树 → 右子树 → 根节点。这种顺序确保了在访问当前节点时,其左右子树已经被完全处理。
//不可以使用其他遍历方式了!
Destroy(root->left);
Destroy(root->right);
erase(root->val);
}3.BST的应用模型
模型一:键模型(k-model)
- 数据结构:
- 节点仅存储键(Key),不直接存储对应的值(Value)。
- 值可能通过其他方式关联,例如:
- 存储在外部数组 / 哈希表中,通过键的索引间接访问。
- 在数据库场景中,键对应磁盘地址或行指针。
- 典型应用场景:
- 数据库索引:B 树(BST 的变种)常用于存储索引键,值对应数据行的物理位置。
- 快速查找集合:如内存中的有序集合(Set),用于快速判断元素是否存在。
- 排序与去重:利用 BST 的有序性,高效实现排序或去重功能。
- 优缺点:
- 优点:
- 节点结构简单,内存占用低。
- 适合 “只关心键是否存在” 的场景。
- 缺点:
- 无法直接通过树结构获取值,需额外逻辑关联。
- 不适合需要频繁更新值的场景。
- 优点:
模型二:键值模型(k-v model)
- 数据结构:
- 节点同时存储键(Key)和对应的值(Value)。
- 值可以是任意类型(如整数、对象、指针等)。
- 典型应用场景:
- 字典(Map):C++ 的
std::map支持高效的键值查询。 - 缓存系统:通过键快速查找缓存数据(如 LRU 缓存的有序结构)。
- 配置管理:存储键值对形式的配置参数。
- 字典(Map):C++ 的
- 优缺点:
- 优点:
- 直接通过键获取值,操作简单。
- 适合需要频繁读写键值对的场景。
- 缺点:
- 节点内存占用更高(需存储值)。
- 若值为大型对象,可能影响缓存局部性。
- 优点:





















 138
138

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








