旅行商问题

旅行商问题（Traveling Salesman Problem, TSP）是经典的组合优化问题之一。该问题要求一个旅行商访问一组城市各一次，最后回到起点城市，且要求路径总长度最短。TSP 是一个 NP 完全问题，对于较大规模的问题，难以找到精确解。然而，对于较小规模的问题，可以使用动态规划（Dynamic Programming, DP）来求解。

#include <stdio.h>
#include <limits.h>
#include <stdbool.h>

#define MAX_CITIES 10

// 打印路径
void printPath(int path[], int n) {
    for (int i = 0; i < n; i++) {
        printf("%d ", path[i]);
    }
    printf("%d\n", path[0]); // 回到起点
}

// 旅行商问题的记忆化递归函数
int tspMemo(int dist[MAX_CITIES][MAX_CITIES], int n, int visited[], int pos, int path[], int cost, int memo[MAX_CITIES][1 << MAX_CITIES]) {
    int state = 0;
    for (int i = 0; i < n; i++) {
        state = (state << 1) | visited[i];
    }
    
    if (memo[pos][state] != -1) {
        return memo[pos][state];
    }
    
    if (pos == n) {
        path[n] = 0; // 标记路径终点
        memo[pos][state] = cost + dist[pos][0]; // 回到起点并存储结果
        return memo[pos][state];
    }
    
    int minCost = INT_MAX;
    for (int city = 1; city < n; city++) { // 从1开始，因为0已经被访问
        if (!visited[city]) {
            visited[city] = true; // 标记城市为已访问
            path[pos + 1] = city; // 记录路径
            int newCost = tspMemo(dist, n, visited, pos + 1, path, cost + dist[pos][city], memo);
            if (newCost < minCost) {
                minCost = newCost;
            }
            visited[city] = false; // 回溯，标记城市为未访问
        }
    }
    
    memo[pos][state] = minCost; // 存储结果
    return minCost;
}

int main() {
    int n;
    printf("输入城市数量: ");
    scanf("%d", &n);

    int dist[MAX_CITIES][MAX_CITIES];
    printf("输入城市间的距离矩阵:\n");
    for (int i = 0; i < n; i++) {
        for (int j = 0; j < n; j++) {
            scanf("%d", &dist[i][j]);
        }
    }

    // 初始化记忆化数组为 -1（表示未计算）
    int memo[MAX_CITIES][1 << MAX_CITIES];
    for (int i = 0; i < MAX_CITIES; i++) {
        for (int j = 0; j < (1 << MAX_CITIES); j++) {
            memo[i][j] = -1;
        }
    }

    int visited[MAX_CITIES] = {false};
    visited[0] = true; // 从城市 0 开始
    int path[MAX_CITIES + 1];
    int minCost = tspMemo(dist, n, visited, 0, path, 0, memo);

    printf("最短路径长度: %d\n", minCost);
    printf("最短路径: ");
    printPath(path, n);

    return 0;
}

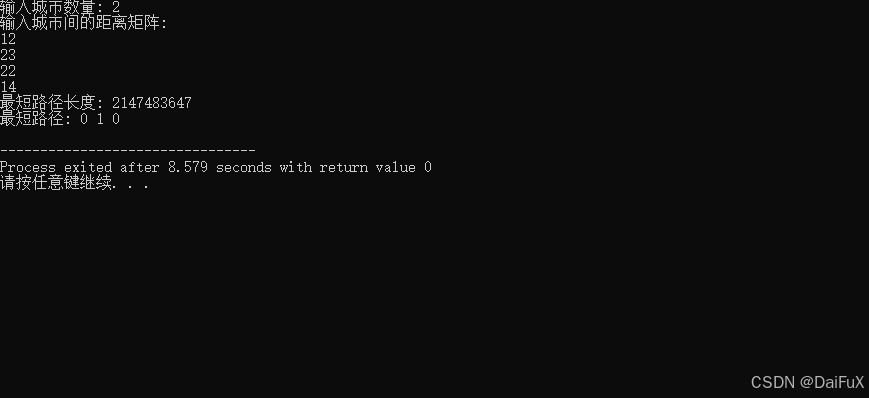
运行结果：