排序算法-选择排序

选择排序是一种简单直观的排序算法，其核心思想是每次从未排序的部分中选出最小（或最大）的元素，放到已排序部分的末尾。

选择排序步骤

1. 初始化：将序列分为已排序部分（初始为空）和未排序部分（初始为整个序列）。

2. 查找最小值：遍历未排序部分，找到最小的元素。

3. 交换位置：将最小元素与未排序部分的第一个元素交换，将其纳入已排序部分。

4. 重复过程：重复上述步骤，直到未排序部分为空。

代码实现

package Sort;

public class SelectionSort {
    public static void main(String[] args) {
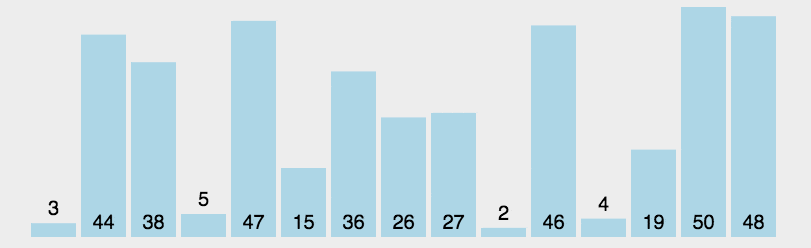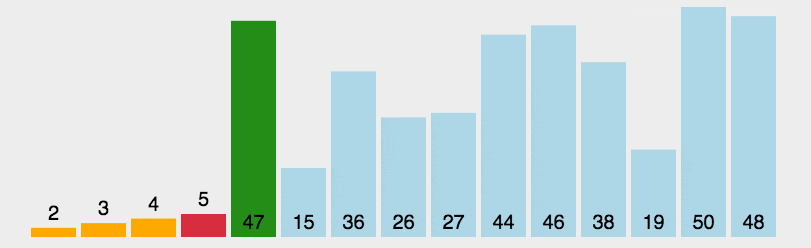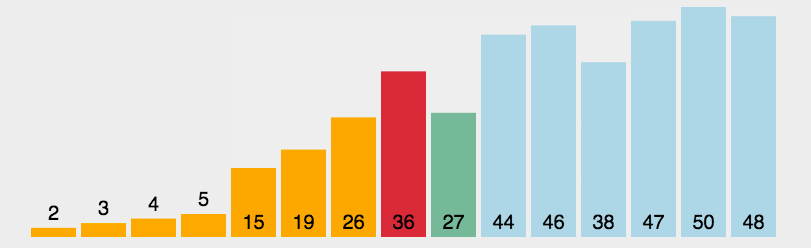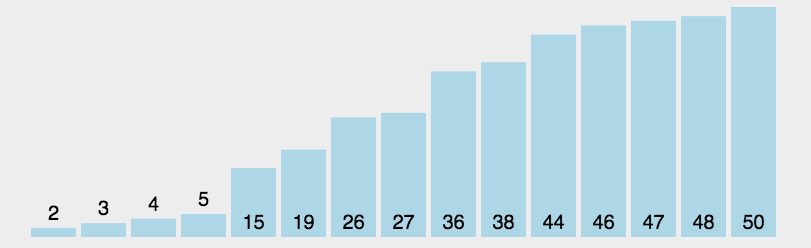
        int[] res = getSelectionSort(new int[]{3,44,38,5,47,15,36,26,27,2,46,4,19,50,48});
        for (int i = 0; i < res.length; i++) {
            System.out.print(res[i] + " ");
        }
    }
    //升序排列，查找最小值，如果降序排列，则查找最大值
    public static int[] getSelectionSort(int[] nums){
        int len = nums.length;
        for (int i = 0; i < len; i++) {
            int minIndex = i;//最小数的下标，每次循环开始总是假设第一个数最小
            for (int j = i+1; j < len; j++) {//每次循环，查找剩余的数的最小值
                if (nums[j] < nums[minIndex]){
                    minIndex = j; //将最小数的小标保存
                }
            }
            //退出内循环，则说明找到剩余数的最小值
            //将当前数与最小值进行交换
            int temp = nums[minIndex];
            nums[minIndex] = nums[i];
            nums[i] = temp;
        }
        return nums;
    }
}

时间复杂度

1. 最坏情况：无论输入是否有序，每次都需要完整遍历未排序部分。

   • 比较次数：(n-1) + (n-2) + ... + 1 = n(n-1)/2，即 O(n²)。

   • 交换次数：每次遍历最多交换一次，共 n-1 次，即 O(n)。

2. 最好情况：即使序列已经有序，仍需完成所有比较，因此仍是 O(n²)。

3. 平均情况：时间复杂度为 O(n²)。

空间复杂度

• 选择排序是原地排序，仅需常数级额外空间（用于临时交换），因此空间复杂度为 O(1)。