GeoGebra：动态数学平台与函数绘图工具

GeoGebra：多领域融合的动态数学平台深度解析

一、软件概览：多领域融合的动态数学平台

GeoGebra是一款免费开源的跨平台动态数学软件，由美国佛罗里达亚特兰大学数学教授Markus Hohenwarter于2001年设计，最初作为其硕士论文课题，后在博士阶段持续完善。其名称融合了“Geometry”（几何）和“Algebra”（代数），体现了核心设计理念——打破数学分支的界限，将几何、代数、微积分、统计及概率等学科整合到统一界面中。截至2025年，其全球用户量已达数百万，支持数十种语言，并斩获多项国际教育软件大奖。

技术架构与版本迭代
基于Java开发，GeoGebra凭借动态输出效果流畅、图形渲染精准获得用户赞誉。软件持续更新，2025年6月发布的6.0.892.0版本安装包约112MB，支持Windows、macOS、Linux系统，并提供iOS和Android移动端适配。其模块化设计分为三大交互窗口：

• 几何窗口：通过工具栏绘制点、线、圆锥曲线等对象，实时联动代数属性；
• 代数窗口：输入函数或方程后自动生成几何图形，对象按“自由”与“派生”分类管理；
• 工作表窗口：类似Excel的单元格结构（如A1），支持数据计算与图形映射。

二、核心功能详解：从基础作图到高级计算

点击 "打开计算器" 即可

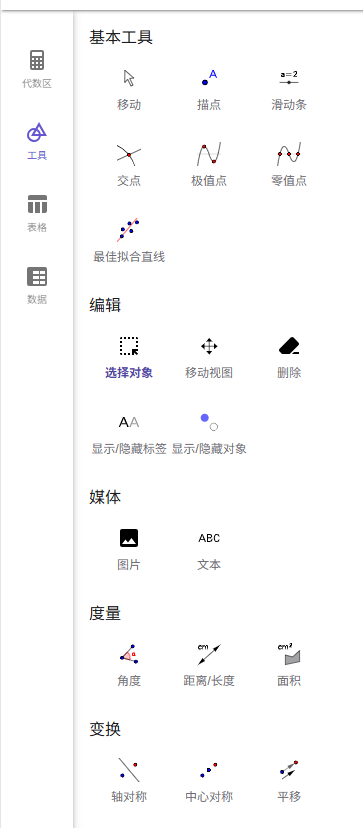
1. 几何与图形

• 动态构造：通过拖拽改变点、线、多边形位置，关联对象（如垂直线、切线）自动更新；
• 高级工具：支持圆锥曲线绘制（输入焦点与点生成双曲线）、极线反演、定长线段（支持变量输入）；
• 变换操作：轴对称、旋转、平移等功能，派生图形随原对象动态变化。

2. 代数与函数

• 实时关联：输入f(x)=x^2-3x后几何区自动生成抛物线，修改代数式即调整图形；
• 符号计算：求导（如f'(x)）、积分、方程求根、极值点分析；
• 命令框功能：直接输入Tangent(f,2)生成函数在x=2处的切线。

3. 统计与数据处理

• 可视化工具：散点图、箱线图、概率分布模型（如正态曲线）；
• 统计分析：计算均值、方差、相关系数；通过“最佳拟合直线”实现线性回归。

4. 3D与高等数学

• 空间建模：绘制参数曲面、空间曲线，支持旋转视图；
• 微积分应用：计算极限、泰勒展开，可视化矢量场。

下表总结了GeoGebra的核心功能模块及其教育应用场景：

功能模块	核心能力	典型教育应用
几何与作图	动态构造、变换操作、高级工具（圆锥曲线、极线）	平面几何证明、立体几何演示、尺规作图模拟
代数与函数	实时关联图形、符号计算、命令输入	函数性质探索、方程求解、导数与积分可视化
统计与概率	数据可视化、统计分析、回归模型	数据分布展示、概率实验、统计假设验证
高等数学	3D建模、微积分运算、向量分析	空间解析几何、多元微积分演示、线性代数辅助

三、软件特色：教育价值与技术创新

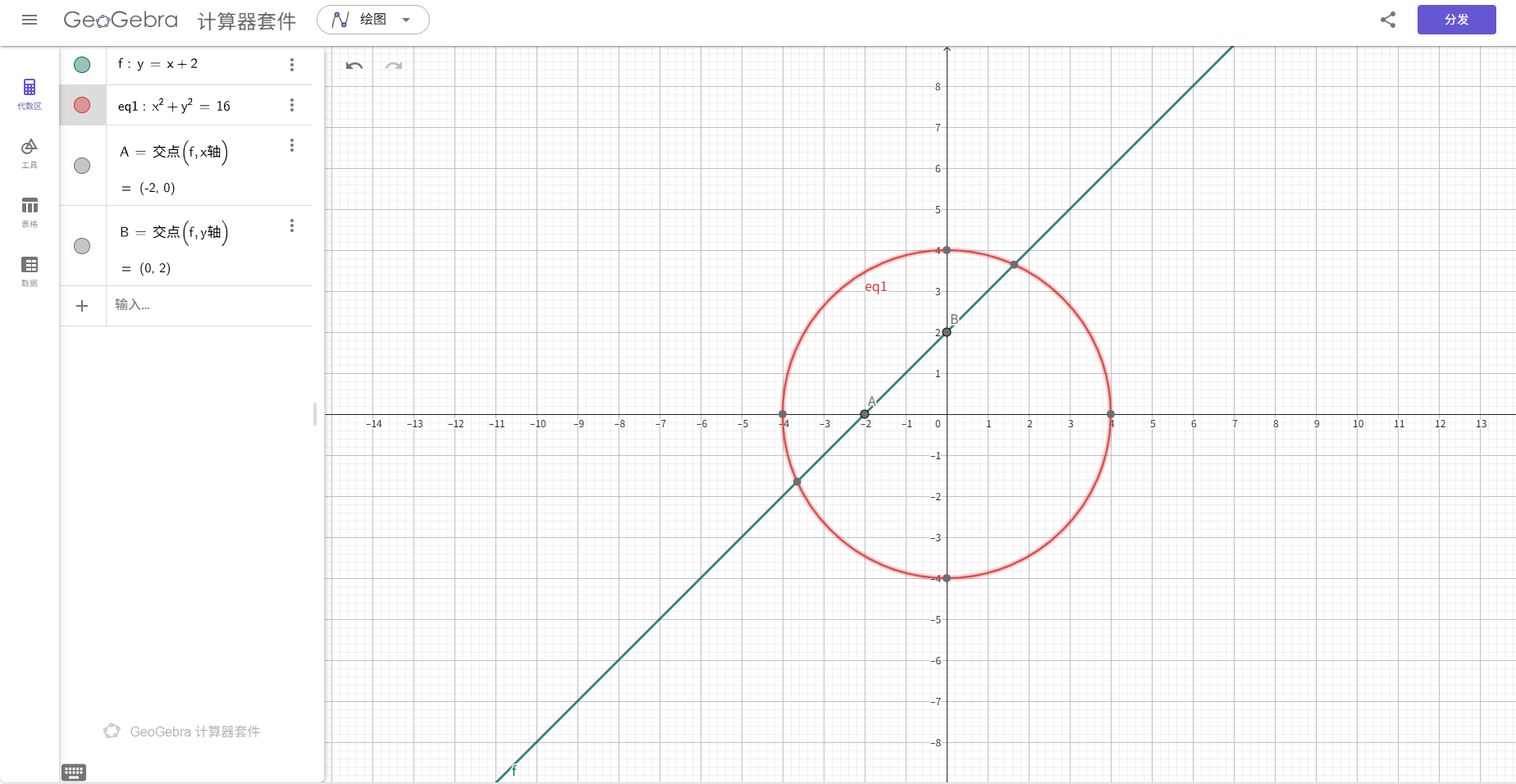
• 动态互联性：对象属性在几何、代数、表格间实时同步，如移动三角形顶点时，其边长方程与面积数值自动更新；
• 低门槛高拓展：初学者无需编程即可绘制基础图形；进阶用户可通过自定义工具创建贝塞尔曲线等复杂模型，或使用脚本开发互动课件；
• 教育资源生态：内置GeoGebraTube平台，共享全球教师创建的百万级免费素材，如互动习题、模拟实验；
• 多平台覆盖：除桌面端外，移动App支持课堂扫码互动，网页版无需安装即可使用。

下表对比了GeoGebra的技术特点及其教育意义：

技术特点	实现方式	教育价值
动态互联	对象属性在几何、代数、表格间实时同步	帮助学生理解数学概念的多元表示，强化抽象与直观联系
社区资源共享	GeoGebraTube平台集成全球数百万教学资源	减少教师备课时间，促进跨文化教学交流
跨平台支持	桌面端、网页版、移动App数据互通	支持混合式学习，实现课堂与自主学习的无缝衔接
自定义工具	创建个性化绘图工具并分享到工具栏	培养计算思维，鼓励创新教学方法

四、应用场景：从课堂到科研

1. 教学支持

• 教师：制作动态课件（如展示圆锥曲线定义），生成带步骤导航的探究任务；
• 学生：验证几何定理（如勾股定理）、模拟概率实验（投针实验估算π值）。

2. 专业研究

• 工程建模：分析机械连杆运动轨迹；
• 数据科学：拟合疫情传播曲线并预测拐点。

3. 测评与协作

• 自动评分：设置条件约束（如“线段AB长度固定”），系统检测学生构造是否符合要求；
• 云端协作：多人实时编辑同一模型，支持注释与版本追踪。

五、获取与资源

• 官方下载：访问官网或可信渠道（如FilePuma）获取最新版，安装包经60余款杀毒软件检测，标记为“Clean”；
• 学习资源：
  • 中文教程整合版含数百个实例（如心脏线绘制、傅里叶变换演示）；
  • Wiki社区提供开放式指南，支持用户贡献内容。

教育实践案例：
某中学教师利用滑动条变量演示二次函数参数变化对图像的影响：拖动参数a时，学生直观观察抛物线开口从向上转为向下的临界点，同步更新的代数式强化了符号与图形的关联。

六、结语

GeoGebra通过技术 democratization革新了数学学习范式，将抽象符号转化为可操作对象，使数学探索变得直观且充满趣味。其开源特性持续推动教育公平，而全球社区的共创生态则成为STEM教育创新的重要引擎。正如一位教师所言：“它让数学从黑板上的静态公式，变成了学生手中活的实验。”