转自 http://blog.ednchina.com/yrwusignal/288071/message.aspx
http://blog.youkuaiyun.com/dznlong/archive/2008/04/08/2261150.aspx
傅里叶分析可以说是信号处理最重要的基石之一。但傅里叶级数、傅里叶变换、离散时间傅里叶变换、离散傅里叶变换等几个有点像又有点不像的概念,不仅经常搞得初学者晕头转向,有时候让老手也有点糊涂。
根据原信号的不同类型,我们可以把傅立叶变换分为四种类别:
|
1
|
非周期性连续信号
|
傅立叶变换(Fourier Transform)
|
|
2
|
周期性连续信号
|
傅立叶级数(Fourier Series)
|
|
3
|
非周期性离散信号
|
离散时域傅立叶变换(Discrete Time Fourier Transform)
|
|
4
|
周期性离散信号
|
离散傅立叶变换(Discrete Fourier Transform)
|
下图是四种原信号图例:

1、 傅里叶级数 -- 周期连续信号的傅里叶分析
在高等数学中就已经知道,在满足一定的条件下,任何一个周期信号都可以分解为正弦信号的叠加。在高等数学中,这种分解就叫傅里叶级数。在信号处理学习的最初阶段,也是从这个概念出发,开始输入到信号处理的傅里叶世界。在信号处理中,周期连续信号的傅里叶分析称为傅里叶级数。此时,在傅里叶分析之前,信号是周期,连续的,在之后,结果是离散的。
定义 设
![]() 是
是
![]() 上以
上以
![]() 为周期的函数,且
为周期的函数,且
![]() 在
在
![]() 上绝对可积,称形如
上绝对可积,称形如
![]()
的函数项级数为
![]() 的 Fourier级数 或三角级数 (
的 Fourier级数 或三角级数 (
![]() 的 Fourier展开式),其中
的 Fourier展开式),其中
![]() ,
,
![]() ,
,
![]()
记为
![]()
以
![]() 为周期的函数的Fourier级数
为周期的函数的Fourier级数
设
![]() 是以
是以
![]() 为周期的函数,令
为周期的函数,令
![]()
可以把
![]() 变换成以
变换成以
![]() 为周期的t 的函数
为周期的t 的函数
![]() 。若
。若
![]() 在
在
![]() 一可积,则
一可积,则
![]() 在
在
![]() 上可积,且
上可积,且
![]() 的Fourier级数展开式是
的Fourier级数展开式是
![]() (1)
(1)
其中
 (2)
(2)
因为
![]() ,所以
,所以
![]() ,于是由(1)(2)分别得
,于是由(1)(2)分别得
![]() (3)
(3)
与
 (4)
(4)
这里(4)式是以
![]() 为周期的函数
为周期的函数
![]() 的Fourier系数,(3)式是
的Fourier系数,(3)式是
![]() 的Fourier级数。
的Fourier级数。
2、 傅里叶变换 -- 非周期连续信号的傅里叶分析
对于连续信号,如果信号不是周期的,其傅里叶分析结果又是如何呢?非周期信号可以等效为周期为无穷大的周期信号。于是,由傅里叶级数出发,利用极限的有关概念,可以推导出非周期信号的傅里叶分析结果,这就是傅里叶变换。再啰嗦一句,非周期连续信号的傅里叶分析称为傅里叶变换。在傅里叶分析之前,信号是非周期的,连续的,在之后,结果也是连续的。
对于非周期信号
![]()

前者是由信号的时间函数变换成频率函数,称为傅里叶正变换式,有时记为
![]() 或
或
![]()
后者是由信号的频率函数变换为时间函数,称为傅里叶反变换式。有时记为
![]() 或
或
![]()
如果上述变换中的自变量不用角频率
![]() 而用频率
而用频率
![]() ,则由于
,则由于
![]() ,可写为
,可写为

频谱密度函数
![]() 是一复变函数,可以写为
是一复变函数,可以写为
![]()
式中
![]() 和
和
![]() 分别为
分别为
![]() 的模和相位,
的模和相位,
![]() 和
和
![]() 分别为
分别为
![]() 的实部和虚部。
的实部和虚部。
傅里叶反变换式也可写成

可见一个非周期信号
![]() 也可以分解成许多不同频率的正、余弦分量,也可以分解为t 的复变函数。若
也可以分解成许多不同频率的正、余弦分量,也可以分解为t 的复变函数。若
![]() 是实函数,则
是实函数,则
![]() 和
和
![]() 分别是ω的偶函数和奇函数,并且
分别是ω的偶函数和奇函数,并且
![]()
3、 离散时间傅里叶变换 -- 非周期离散信号的傅里叶分析
傅里叶级数和傅里叶变换都是针对连续信号而言的,那么对于数字信号而言,是否有对应的傅里叶分析呢?答案是肯定的,这就是离散时间傅里叶变换( DTFT )和离散傅里叶变换( DFT )。
对非周期离散信号的傅里叶分析称为离散时间傅里叶变换。在傅里叶分析之前,信号是非周期的,离散的,在之后,结果是连续的。
记连续时间信号f (t ) 的采样为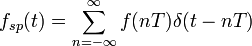 , 其傅里叶变换 为
, 其傅里叶变换 为
这就是采样序列f (n T ) 的DTFT:
为方便起见,通常将采样间隔T归一化,则有
上式即为f (n ) 的离散时间傅里叶变换 。 它的反变换 为:
考虑到DTFT的周期性(参见频 谱周期性 ),它的逆变换实际上是以周期的连续函数作为输入,离散的谱作为输出,这正是傅里叶级数 的形式。
4、 离散傅里叶变换 -- 周期离散信号的傅里叶分析
对周期离散信号的傅里叶分析称为离散傅里叶变换。在傅里叶分析之前,信号是周期的,离散的,在之后,结果是离散的。如果按照前面三种分析的命名,离散傅里叶变换叫离散傅里叶级数似乎更为妥当。但由于历史的原因,大家习惯把这种傅里叶分析称为离散傅里叶变换。当然,关于 DFT 是否隐含着信号周期性的问题,也有一些争论。有的认为进行 DFT 分析就意味着默认离散信号是周期的,有的则认为离散信号不一定要看成是周期的。此处采取默认离散信号周期性的说法,主要是基于如下理由:如果把 DFT 看做是对 DTFT 结果在频域的采样的话,那么根据信号系统的有关理论可知,频域的采样等效于时域的周期延拓,这样,离散信号自然变成周期的了。在实际分析中,将 DFT 看做是对 DTFT 结果在频域的采样是合乎情理的。
下面给出离散傅里叶变换的变换对:
-
离散傅里叶变换的逆变换(IDFT)为:
-
-
可以记为:
-
-
实际上,DFT和IDFT变换式中和式前面的归一化系数并不重要。在上面的定义中,DFT和IDFT前的系数分别为
1 和
1/N 。 有时会将这两个系数都改成
 。
。
-
这上面的四个与傅里叶分析有关的概念,最重要的是 DFT 。因为前面三种分析都需要假定信号的时域及频域都是无限长的。从概念上讲,虽然 DFT 也需要时域频域无限长,但由于时域频域都是周期的,因此只需要一个周期的信息即可。另外,由于计算机等数字设备只能 处理数字信号,也即是要求无论是时域还是频域,都要是离散的。因此, DFT 在实践中占有最重要的地位。傅里叶级数,傅里叶变换,离散时间傅里叶变换 这三个概念则更多的用于理论分析中。





 本文详细介绍了傅里叶分析的基本概念,包括傅里叶级数、傅里叶变换、离散时间傅里叶变换和离散傅里叶变换。着重解释了非周期性连续信号、周期性连续信号、非周期性离散信号和周期性离散信号的傅里叶分析方法,以及它们在信号处理领域的应用。
本文详细介绍了傅里叶分析的基本概念,包括傅里叶级数、傅里叶变换、离散时间傅里叶变换和离散傅里叶变换。着重解释了非周期性连续信号、周期性连续信号、非周期性离散信号和周期性离散信号的傅里叶分析方法,以及它们在信号处理领域的应用。
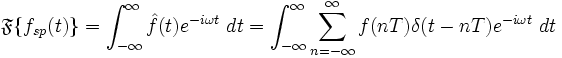
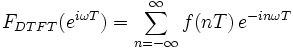
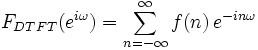

![/left/{x[n]/right/}_{0/le n
<N}](http://upload.wikimedia.org/math/c/6/b/c6be1886740cf9409e570f1e9360cc81.png) , 它的离散傅里叶变换(DFT)为
, 它的离散傅里叶变换(DFT)为
![/hat{x}[k]=/sum_{n=0}^{N-1}
e^{-i/frac{2/pi}{N}nk}x[n] /qquad k = 0,1,/ldots,N-1.](http://upload.wikimedia.org/math/6/5/9/659ff6c8772ea9fd9fa0e78ef4713582.png)
 表 示这一变换,即
表 示这一变换,即

![x/left[n/right]={1 /over N}/sum_{k=0}^{N-1}
e^{ i/frac{2/pi}{N}nk}/hat{x}[k] /qquad n = 0,1,/ldots,N-1.](http://upload.wikimedia.org/math/4/d/e/4de19047754aed0bda0c230d32fa4ace.png)

















 557
557

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








