7.1.4 学习的对偶算法
求解线性可分支持向量机的最优化问题:
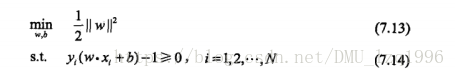
运用拉格朗日对偶性,求解对偶问题得到原始问题的解。
拉格朗日对偶问题:https://blog.youkuaiyun.com/blackyuanc/article/details/67640844

(1)利用w,b求min L(w,b,a)
(2)求min(w,b,a)对a的极大
对偶问题的解与原始问题的解之间的关系:


线性可分支持向量机学习算法:

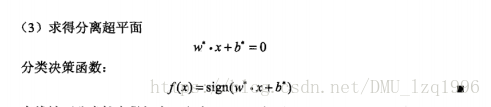
由a得出支持向量的概念:

7.2 线性支持向量机与软间隔最大化
7.2.1 线性支持向量机(线性不可分时的线性支持向量机)
线性不可分问题——软间隔:函数间隔加上松弛变量;目标函数加上惩罚参数C
硬间隔最大化——软间隔最大化:


7.2.2 学习的对偶算法
如何求解w,b的值:



对偶问题的解与原始问题解的关系:
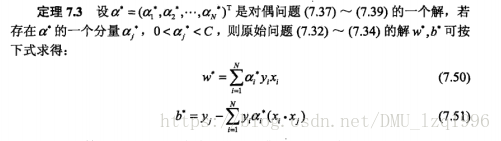
线性支持向量机学习算法:

7.2.3 支持向量
支持向量与a和C的关系:
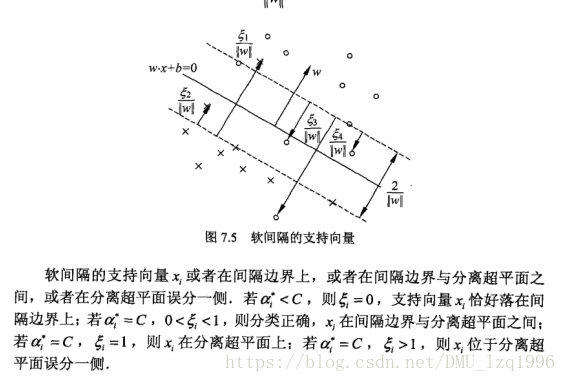
参考:(软间隔的支持向量问题)https://blog.youkuaiyun.com/qq_34993631/article/details/79340747
7.2.4 合页损失函数

合页损失函数:
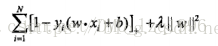
合页损失函数与0-1损失函数和感知机损失函数的图像:
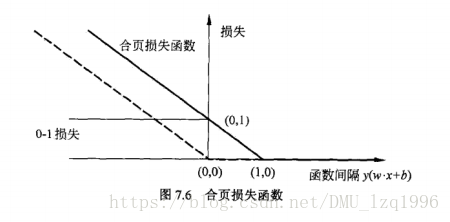





 本文探讨了支持向量机(SVM)的学习算法,包括线性可分与线性不可分情况下的SVM,讲解了拉格朗日对偶性在求解最优化问题中的应用,介绍了软间隔最大化及合页损失函数的概念。
本文探讨了支持向量机(SVM)的学习算法,包括线性可分与线性不可分情况下的SVM,讲解了拉格朗日对偶性在求解最优化问题中的应用,介绍了软间隔最大化及合页损失函数的概念。

















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








