KMP 字符串总结（看毛片）

原创于 2023-09-05 00:46:27 发布 · 717 阅读

0 ·

CC 4.0 BY-SA版权

文章标签：

#算法 #c++ #数据结构

文章介绍了如何使用next数组来计算给定模式串P在字符串S中所有出现的位置的起始下标，通过动态规划找到最长公共前后缀来确定匹配位置。

给定字符串 S （长度为M）一个模式串 P

模式串 P （长度为N），在字符串 S 中多次作为子串出现。求出模式串 P在字符串 S 中所有出现的位置的起始下标。

数据范围

1≤N≤10e5
1≤M≤10e6

为了写代码便利，下标均从1开始。

eg: 1 2 3 4 5 6 7 8

S A B A B A B C

P A B A B A B A B

ne 0 0 1 2 3 4 5 6

一：此处需要建立一个 next[ j ]数组, next[ j ] 用来记录 p[1, j] 的前缀和后缀最大长度即 p[1, next[ j ] ] = p[ j - next[ j ]+1 , j ]

手动模拟： next[1] 前缀：空集后缀：空集 0

next[2] 前缀： { A } 后缀： { B } 0

next[3] 前缀： {A, AB} 后缀： {A,BA} 1

next[4] 前缀： {A，AB，ABA} 后缀： {B, AB, BAB} 2

next[5] 前缀：{A, AB, ABA, ABAB} 后缀： {A , BA, ABA, BABA} 3

…… B, AB, BAB, ABAB, BABAB

……

二：匹配思路和代码

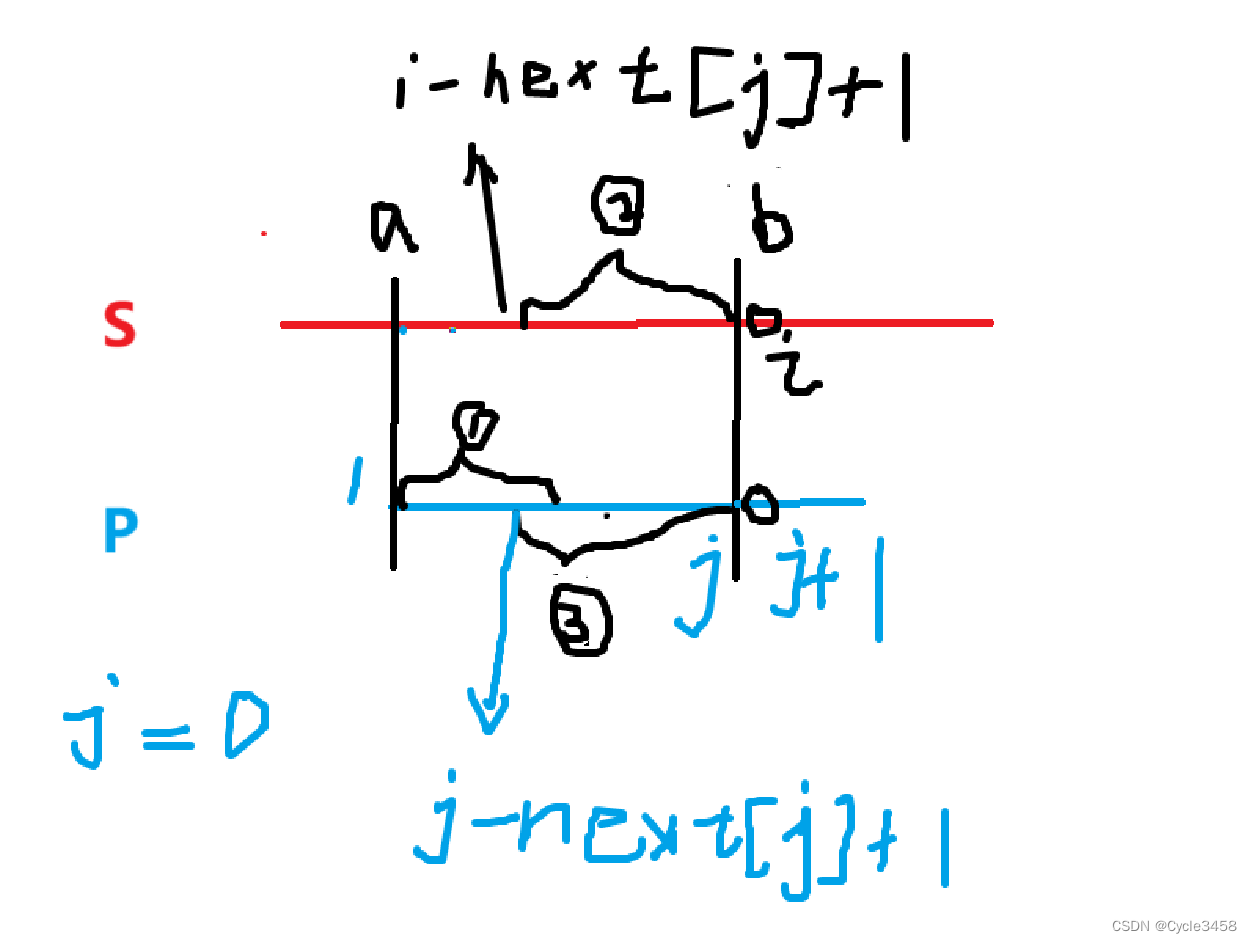
（画图水平有限（doge）

S从a开始匹配到b ,直到位置 i, 此时S[ i ] != P[ j +1] ，注意此时不是将 p的指针j移动至串头，而是直接移动至下次能匹配到的位置，那么这个位置在哪呢，就在next [ j ]里由于1串==3串， 3串== 2串，所以移动p串使1 到3 的位置。即j= next[ j ]

code:

#include <string>
#include <iostream>

using namespace std;
const int N=100010, M=1000010;
char p[N], s[M];  // 1-N
int n,m;
int ne[N];
int main()
{
	cin >> n >> p+1 >> m >> s+1;
	//创建 next 数组 
	ne[1]=0;
	for(int i=2, j=0; i<=n; i++)
	{
		while(j && p[i]!= p[j+1]) j=ne[j];
		if (p[i]==p[j+1]) j++;
		ne[i]=j;
	}
	
	//开始匹配
	for(int i=1,j=0; i<=m; i++)   // i从1 开始， j从0 开始 
	{
		while(j && s[i]!=p[j+1]) j=ne[j];  // j为 0时退出循环， 模式串从头开始匹配 
		if (s[i]==p[j+1]) j++;      
		if(j==n)
		{
			printf("%d ",i-n);
			j=ne[j];
		}
	}
	return 0;
	
}