LeetCode 447. 回旋镖的数量 (排列组合问题)

最新推荐文章于 2024-09-30 05:21:25 发布

原创最新推荐文章于 2024-09-30 05:21:25 发布 · 187 阅读

0 ·

CC 4.0 BY-SA版权

文章标签：

#leetcode #算法 #数据结构

算法题专栏专栏收录该内容

59 篇文章

订阅专栏

该博客探讨了一个算法问题，即如何高效地找出给定点集中三个点的组合，使得任意两点之间的距离相等。博主指出传统的暴力枚举方法效率低下，提出了利用哈希表和排列组合思想进行优化，通过计算距离并存储相同距离点的数量，从而减少时间复杂度到O(n^2)。算法实现包括使用unordered_map存储距离计数，并计算组合总数。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

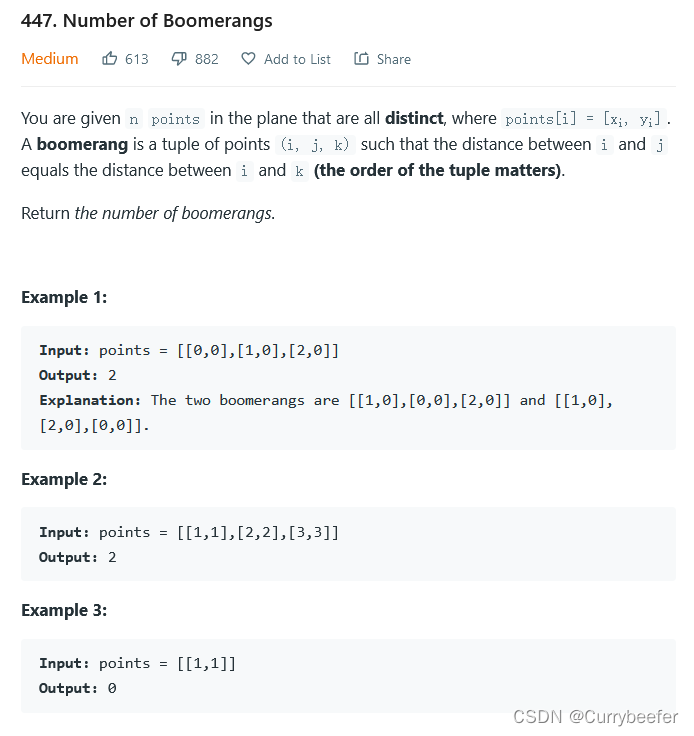
在这里插入图片描述

总的来说就是需要寻找到三个点的组合，i，j，k，其中对于i来说，j和k于i的距离必须相等。
暴力枚举法需要三重循环，这样的话时间复杂度是O(n^3)太不划算了。
因此我们可以想到排列组合问题，思路就是枚举的时候如果将i点固定，在剩下的点中筛选出距离与i相等的点的集合。
假设离i距离为a的点有n个，那么就是从n个里边选出顺序的两个点与i组合，即排列组合问题，An2。
用哈希表存储距离为a的组合数量，相加即可。

int numberOfBoomerangs(vector<vector<int>>& points) 
    {
        int res=0;

        for(int i=0;i<points.size();i++)
        {
            unordered_map<int,int> map;
            for(int j=0;j<points.size();j++)
            {
                int dis=Distance(points[i],points[j]);
                map[dis]++;
            }
            for(auto p=map.begin();p!=map.end();p++)
            {
                res+=p->second*(p->second-1);
            }
        }
        return res;
    }
    
    int Distance(vector<int> a, vector<int> b)
    {
        int x=a[0]-b[0];
        int y=a[1]-b[1];
        
        return x*x+y*y;
    }