相关数学知识

数学相关知识（二）

概率论与数理统计应用实例：

问题分析

在前面的各自10000个路人中，西施貂蝉赢得的回头数目一共三种情况

• 西施的回头数大于貂蝉，假定发生概率为P(A)

• 西施的回头数小于貂蝉，假定发生概率为P(B)

• 西施的回头数等于貂蝉，假定发生概率为P(C)

• 西施貂蝉美貌匹敌，根据对称性，有P(A) = P(B ) = P

  P(C) = 1- 2p

• 假定第10001人的回头概率为X,若貂蝉的总回头数D大于西施的总回头数X，则有

  • 要么A发生
  • 要么C发生，第10001人回头
  • 从而：P(D>X) = P(A) + P(C)*x = p + x - 2p*x

int lookBeauty(double p , int n){
    int c = 0;
    for(int i=0; i< n; i++){
        if((rand()%2)<p)
            c++;
    }
    return c;
}

double Beauty(int N,double p){
    int c = 0;
    for(int i=0; i< N; i++)
    {

        if(lookBeauty(p,10001) >lookBeauty(p,10000))
            c++;
    }
    return (double)c/N;

}
int main ()
{
    int N = 10000;
    double p = 0.9;
    cout << Beauty(N,p) <<endl;
    return 0;
}

---

问题

从1,2,3,……..,98,99,2015这100个数中任意选择若干个数(可能是0个数) 求异或，试求异或的期望值

针对任何一个二进制位，取奇数个1异或后会得到1，取偶数个1异或后会得到0；与取0的个数无关

给定的最大数$2015=（11111011111）_2$ ,共11位

针对每一位分别计算，考虑第i位$X_i$,假定给定的100个数中第i位一共有N个1，M个0，某次采样取到的1 的个数为k

则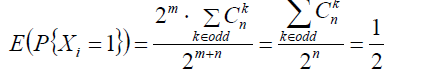

总期望

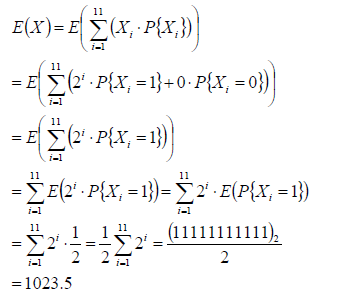
int Sample(const int*a, int size, bool*f)
{

    memset(f, 0, sizeof(bool) *size);
    int N = rand() % (size + 1);
    int n=0;
    while(n < N){
        int t = rand() % size;
        if(!f[t])
        {

            f[t] = true;
            n++;
        }
    }
    n = 0;
    for(int i= 0; i <size; i++)
    {

        if(f[i])
        {
            n ^= a[i];
        }
    }
    return n;
}

int main()
{

    const int N = 100;
    int a[N];
    bool f[N];
    int i;
    for(i = 0; i < N-1; i++)
    {

        a[i] = i+1;
    }

    a[N-1] = 2015;
    int sampleSize = 3000;
    double s = 0;

    for(i = 0; i <sampleSize; i++)
    {
         s  += Sample(a, N, f);
    }



    cout <<s <<endl;
    s /= sampleSize;
    cout <<s<<endl;
    return 0;
}