数据结构 第五章 二叉树 (先序遍历中序遍历递归迭代实现;层次遍历)

树

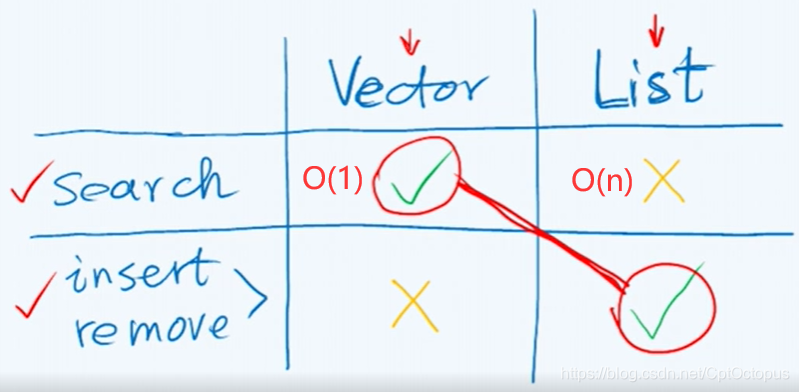
向量和列表无法兼顾查找(静态操作)和插入移动(动态操作)，树结构可以兼顾

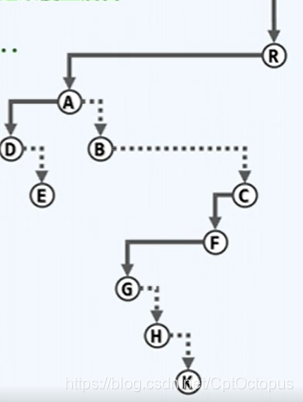
用二叉树表示多叉树

多叉树可以通过长子-兄弟法转化为二叉树，长子兄弟法为“左长右兄”

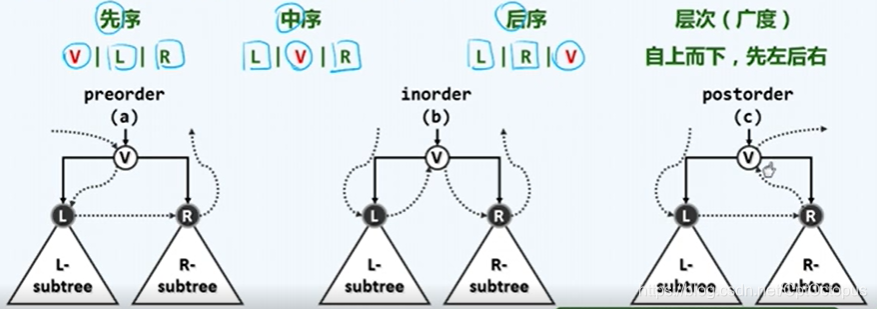
先序遍历

先序，中序，后序遍历的区别是先遍历根节点还是先左右子树

先序遍历递归实现

template <>typename T,typename VST>//T为当前结点模板类型，VST为当前结点数据模板类型
void traverse(BinNodePose(T) x,VST &visit){
if(!x)return;
visit(x->data);//访问当前结点数据
traverse(x->lChild,visit);
traverse(x->RChild,visit);
}

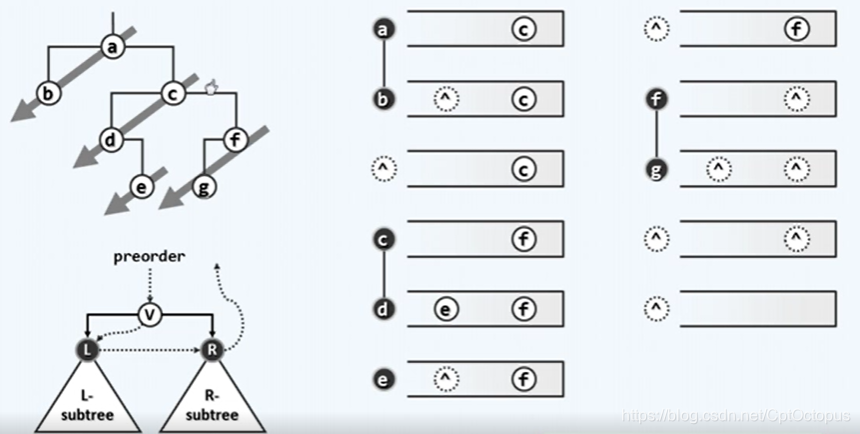
先序遍历迭代实现

先自顶而下的访问左结点，将每个左结点的右结点压入栈，再自低而上的访问右结点,访问右结点时，把该右结点当成新的根结点，并对该右结点(根结点)执行之前同样的leftbranch操作

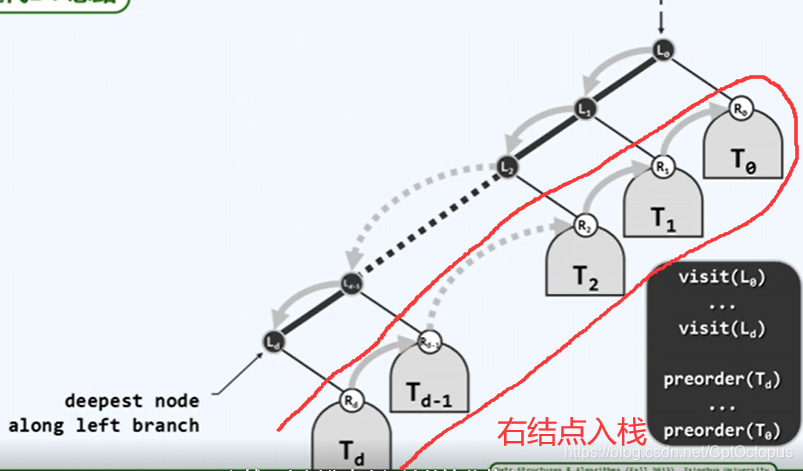
template <>typename T,typename VST>//左链函数
static void visitAlongLeftBranch(BinNodePose(T) x,VST &visit,Stack<BinNodePose(T)> &S)
{
while(x)
	{
	visit(x->data);//访问当前结点的数据
	S.push(x->rChild);//将右孩子入栈，将来逆序出栈
	x->xlChild;//沿左链下行
	}
}
template <>typename T,typename VST>//主函数
void travPre_I2(BinNodePose(T) x,VST &visit){
Stack<BinNodePose(T)> S;
while(true){
	visitAlongLeftBranch(x,visit,S);
	if(S.empty())break;
	x=S.pop();
	}
}

中序遍历

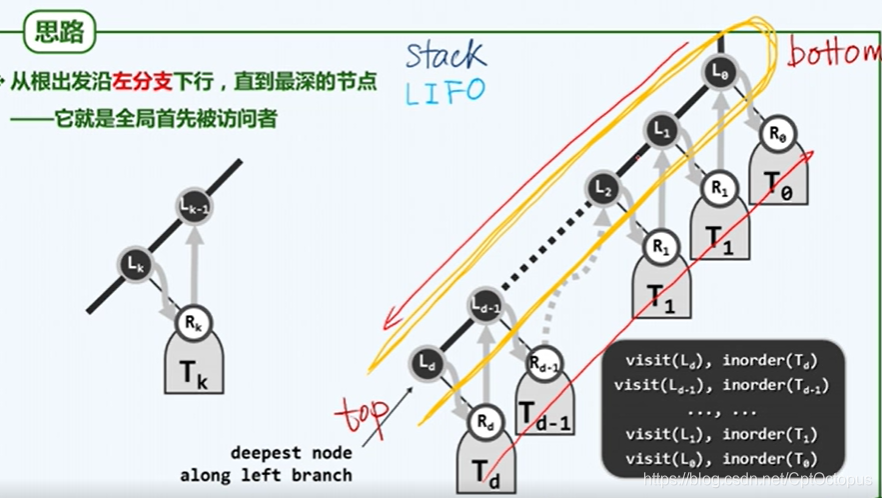
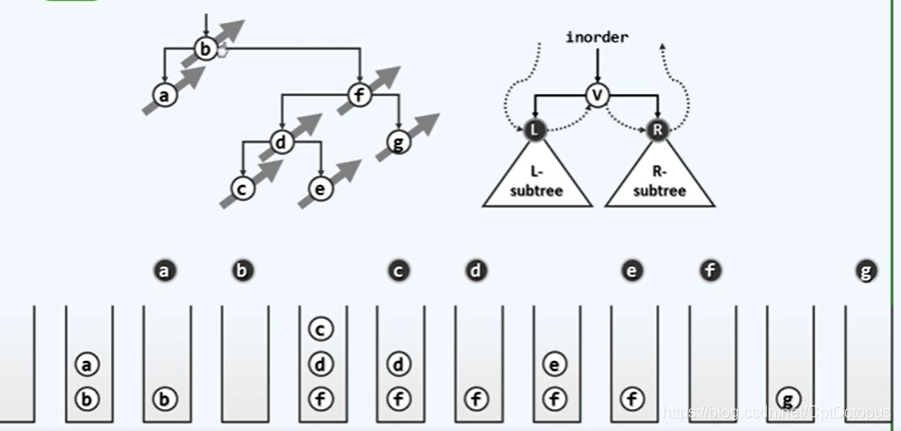
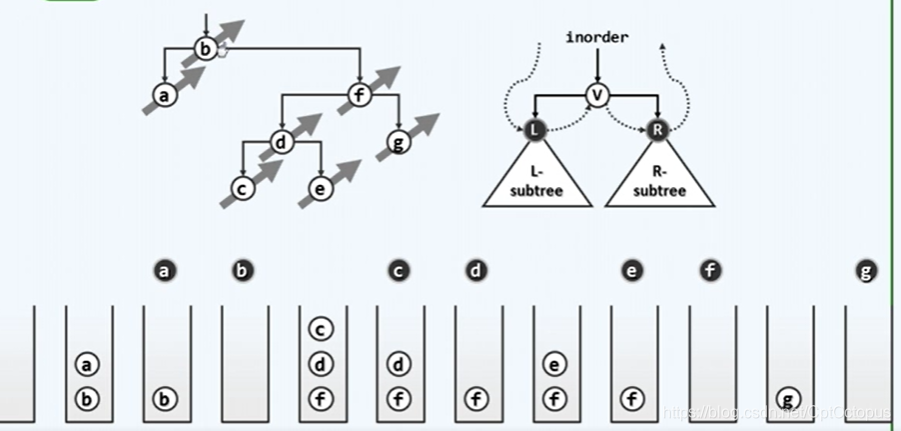
自顶向下把左链结点压入栈，从左链最下端开始，按照弹出左链结点——访问其右结点——再弹出左链结点的顺序依次访问，访问其右结点时把该右节点看做新的根结点，对该根结点(右结点)执行相同的goleftbranch操作

中序遍历递归实现

template <>typename T,typename VST>//T为当前结点模板类型，VST为当前结点数据模板类型
void traverse(BinNodePose(T) x,VST &visit){
if(!x)return;
traverse(x->lChild,visit);
visit(x->data);//访问当前结点数据
traverse(x->RChild,visit);
}

中序遍历迭代实现

template <>typename T,typename VST>//左链函数
static void goAlongLeftBranch(BinNodePose(T) x,VST &visit,Stack<BinNodePose(T)> &S)
{
while(x)
	{
	S.push(x);//将左链入栈，将来逆序出栈
	x->xlChild;//沿左链下行
	}
}
template <>typename T,typename VST>//主函数
void travPre_I2(BinNodePose(T) x,VST &visit){
Stack<BinNodePose(T)> S;
while(true){
	goAlongLeftBranch(x,visit,S);
	if(S.empty())break;
	x=S.pop();
	visit(x->data);
	x=x->rChild;
	}
}

层次遍历

使用队列作为辅助，将左右孩子依次入队，然后出队

template <>typename T,typename VST>//T为当前结点模板类型，VST为当前结点数据模板类型
void BinNode<T>::traverLever(VST & visit){
Queue<BinNodePose(T)> Q;//引入辅助队列
Q.enqueue(this);
while(!Q.empty()){
BinNodePose(T) x = Q.dequeue();
visit(x->data);
if(HaseLeftChild(*x))Q.enqueue(x->lChild);
if(HaseRightChild(*x))Q.enqueue(x->rChild);
}
}

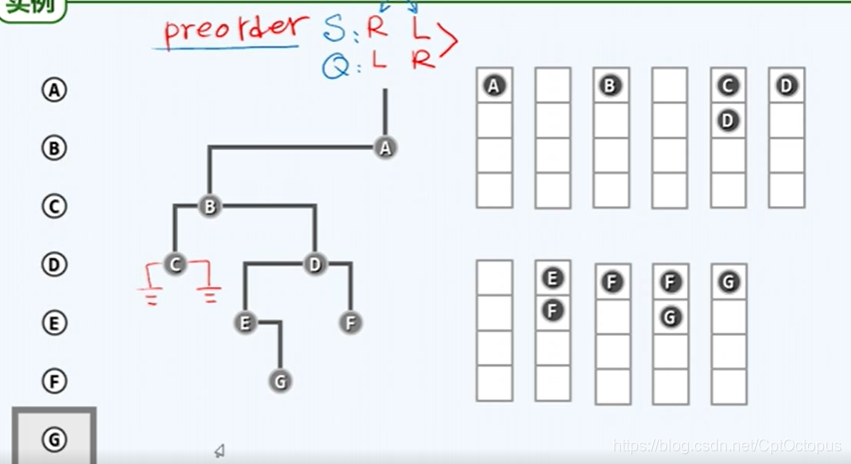
二叉树重构(已知遍历顺序，重构出二叉树)

1）已知先序或者后序，加上中序，可以还原重构任意二叉树
2）已知先序和后序，可以还原重构真二叉树，真二叉树任意度数为偶数，即为0或者2