代数基本概念理解——限制(restriction)

原创于 2025-11-29 18:06:31 发布 · 541 阅读

9 ·

CC 4.0 BY-SA版权

文章标签：

#函数 #函数定义域限制 #函数定义域 #代数

数学与应用数学专栏收录该内容

156 篇文章

订阅专栏

1. 限制的定义

在数学中，一个函数 f 的(定义域)限制(restriction)是一个新的函数，通过为原函数f 选择一个更小的定义域A而获得的，通常表示为 $f{|}_{A}$ 或 $f{\upharpoonright}_{A}$ 表示。即将原函数的定义域缩小至其子集后获得的新函数，其值域保持不变。

令 f : E ⟶ F 为一个从一个集合 E 到另一个集合 F 的函数。若一个集合 A 为集合E的一个子集，则 f 到 A 的限制(即定义域限制到 A ) 是函数

$f{|}_{A}:A \longrightarrow F$ 。

2. 为什么要定义函数的限制？

2.1 限制定义域以定义函数

虽然许多函数(例如指数函数或立方根函数)没有限制，但其他一些函数仅适用于特定集合。因此，它们的正式定义包含一个或多个限制条件。例如：

$\bullet$ 常量函数：c是一个实数( c∈ℝ ) 。

$\bullet$ 线性函数：m ≠ 0 ，换言之，斜率不等于0，它就变成了一个常量函数。

$\bullet$ 对数函数：x > 0 。

$\bullet$ 平方根函数：限制到 x ≥ 0 。

函数的限制通常是由于公式中的代数运算问题造成的。例如，对于比率函数，要注意分母等于零的情况：

-------函数------------------限制---------

$f(x)=\frac{1}{x}$ -------------- x ≠ 0

$f(x)=\frac{1}{x-2}$ ------------ x ≠ 2

$f(x)=\frac{x+1}{x^{2}-1}$ ----------- x ≠ ±1

对于根号函数，不能取负数平方根。

-------函数------------------限制---------

$f (x) = \sqrt{x+3}$ --------------x ≥ -3

2.2 使用函数的限制求反函数

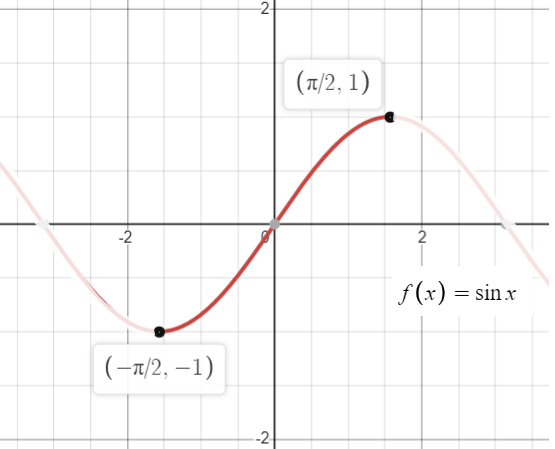
例如，若你设置一个区间 [-π/2 , π/2] ，则正弦函数就成为一对一的(双射的)。

2.3 使用函数的限制使函数有“更佳的行为”

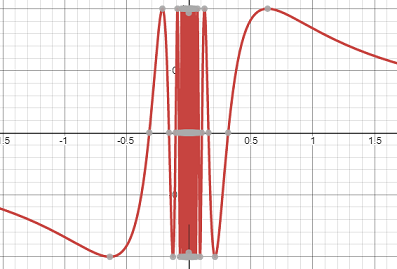
有些函数，例如 f (x) = sin(1/x)，在 x = 0 附近表现很差。因为函数在该点没有定义，所以其值会剧烈波动，几乎无法处理。将定义域缩小到一个较小的区间(不包含零点！)，就能使函数更容易处理。

3. 其它例子

(1) 令φ ：G ⟶ 𝒢 (LaTex语法“mathcal{G}”,Unicode:U+ 1D4A2) 为一个同态群，并令 H 为 G 的一个子群。我们可以将 φ 限定在 H ，从而获得一个同态

$\varphi{|}_{H}: {H} \longrightarrow \mathcal{G}$ 。

这意味着，我们采用相同的映射但限定了其定义域：因此，根据定义，若 h 在 H 中，则 $[\varphi{|}_{H}]( h) = {\varphi}(h)$ 。( 为清晰起见，我们在符号 $\varphi{|}_{H}$ 外层加了方括号。) 加了限定后还是一个同态，因为φ是一个同态 , 而 $[{\varphi}|_{H}]$ 的核是 φ 的核与 H 的交集：

$\ker({\varphi}|_{H}) = \ker(\varphi)\cap{H}$ 。

根据核的定义，这是显然易见的。 $[{\varphi}|_{H}]$ 的像与映射 φ 下的 H 像 φ(H ) 是相同的。

计算方法可能有助于描述这种限定。根据推论(2.8.13),像的阶数整除| H |和| 𝒢 |。若 | H | 和 | 𝒢 |没有公因子，φ(H ) = {1} ，因此，H 包含于核中。

(2) 对于 V 的一个子空间 W ，若其通过算子将其映射到自身，即

TW ⊂ W ，

则称其为不变子空间(invariant (subspace))，或更确切地称为 T不变子空间。换言之，若只要 w 在 W 中，就有T(w) 也在 W 中，则 W 是不变的。这时，T 在 W 上定义了一个线性算子，称其为到W 的限制(restriction)。我们通常将这个限制表示为 $T{|}_{W}$ 。