二叉树的创建以及前序、中序、后序、层次遍历

二叉树的创建

前序序列和中序序列创建二叉树

        我们都知道，二叉树的前序遍历规则和中序遍历规则。

        前序遍历规则为：访问根节点->前序遍历左子树->前序遍历右子树。

        中序遍历规则为：中序遍历左子树->访问根节点->中序遍历右子树。

        我们以下面的二叉树为例，看看，这两种遍历规则有什么联系：

        如图，是一颗二叉树，我们先写出 它的 前序序列和中序序列。

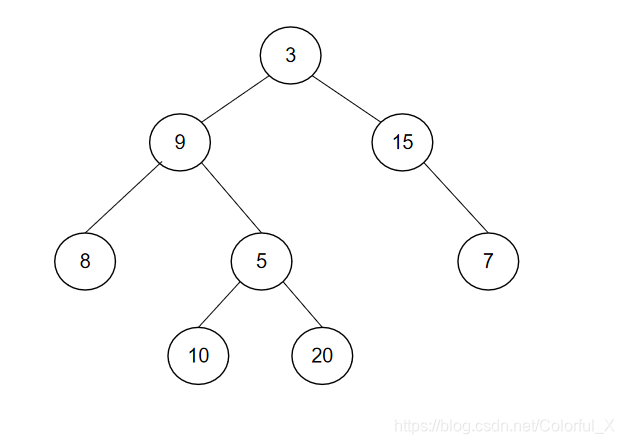
        根据二叉树的前序遍历规则，我们可以写出其前序序列为：{3,9,8,5,10,20,15,7}

        根据二叉树的中序遍历规则，我们可以写出其中序序列为: {8,9,10,5,20,3,15,7}

        此时，我们可以发现，前序序列中的每一个节点对应在中序序列中的所在的位置，其之前都是该节点的左子树包含的所有节点，其之后都是该节点的右子树包含的所有节点。

        举个例子：前序序列中 3 这个节点，其在中序序列中的下标为5，在下标5之前的 8、9、10、5、20这些节点，都是3这个节点的左子树所包含的全部节点，在下标5之后的15、7这些节点，都是3这个节点的右子树所包含的全部节点。

        所以，我们在创建二叉树的时候，就可以利用这个特征来创建。即前序序列中的节点都可以当做一棵二叉树的根节点，根据这个节点在中序序列中的位置，来确定这棵二叉树的左右子树。找到该二叉树的左右子树后，又分别以左右子树的基准，查找左右子树的左右子树的根节点。

        根据上述思路，我们先通过前序序列找到整个二叉树的根节点：3。

        紧接着，查找3在中序序列中的位置，找到为：pos = 5。

        于是我们就可以确定，整个二叉树的左子树的所有节点，都存在于：[is,pos-1]这个区域。右子树的所有节点都存在于：[pos+1,ie]这个区域。

        接着，我们去创建左子树的根节点，但是左子树的根节点去哪拿呢？我们刚才已经说过，前序遍历优先输出的是每一棵二叉树的根节点。但是我们又如何保证前序序列中哪一个区间的数据 是在左半部分，哪一个区间的数据 是在右半部分呢？

        此时，我们可以定义一个dist来确定左半部分和右半部分的数据。int dist = pos - is。我们可以通过这个差值，在前序序列中确定哪一段区间是属于左子树的，哪一段区间是属于右子树的。

        即：[ps,ps+dist]是下一次查找左子树根节点所在的区间（即左前序，就在这个左前序中查找下一棵二叉树的根节点）
               [is,is+dist-1]（即左中序，用于确定下一棵二叉树的左半部分）

               [ps+dist+1,pe]是下一次查找右子树的根节点所在区间（即右前序）

               [is+dis+1,ie]是下一次查找的右中序（用于确定下一棵二叉树的右半部分）

        代码实现：

    public void createPI(int[]pre,int[]in){
   
   
        if (pre.length<1 || in.length <1 || pre==null || in==null || pre.length!=pre.length){
   
   
            return;
        }
        int n= pre.length;
        root = createPI(pre,0,n-1,in,0,n-1);
    }
    private BtNode createPI(int[]pre,int ps,int pe,int[]in,int is,int ie){
   
   
        BtNode s = null;
        if (pe-ps>=0){
   
   
            s = new BtNode(pre[ps]);
            int pos = findIn(in,is,ie,pre[ps]);
            if (pos==-1){
   
   
                return null;
            }
            int dist = pos-is;
            s.leftChild = createPI(pre,ps+1,ps+dist,in,is,is+dist-1);
            s.rightChild = createPI(pre,ps+dist+1,pe,in,is+dist+1,ie);
        }
        return s;
    }

    private int findIn(int[]in,int begin,int end,int val){
   
   
        int pos = -1;
        for (int i = begin; i <=end ; i++) {
   
   
            if (in[i] == val){
   
   
                pos = i;
                break;
            }
        }
        return pos;