对于一个式子,在一个区间内具有相同的值,我们可以把它看成一个块,例如[n/i]([ ]表示向下取整,对应程序就是n/i),对于[1,n]的任何一个数k,它所在的块的右边界是n/(n/k),证明过程如下(图片源自b站董晓算法)

then,我们来看一道题目
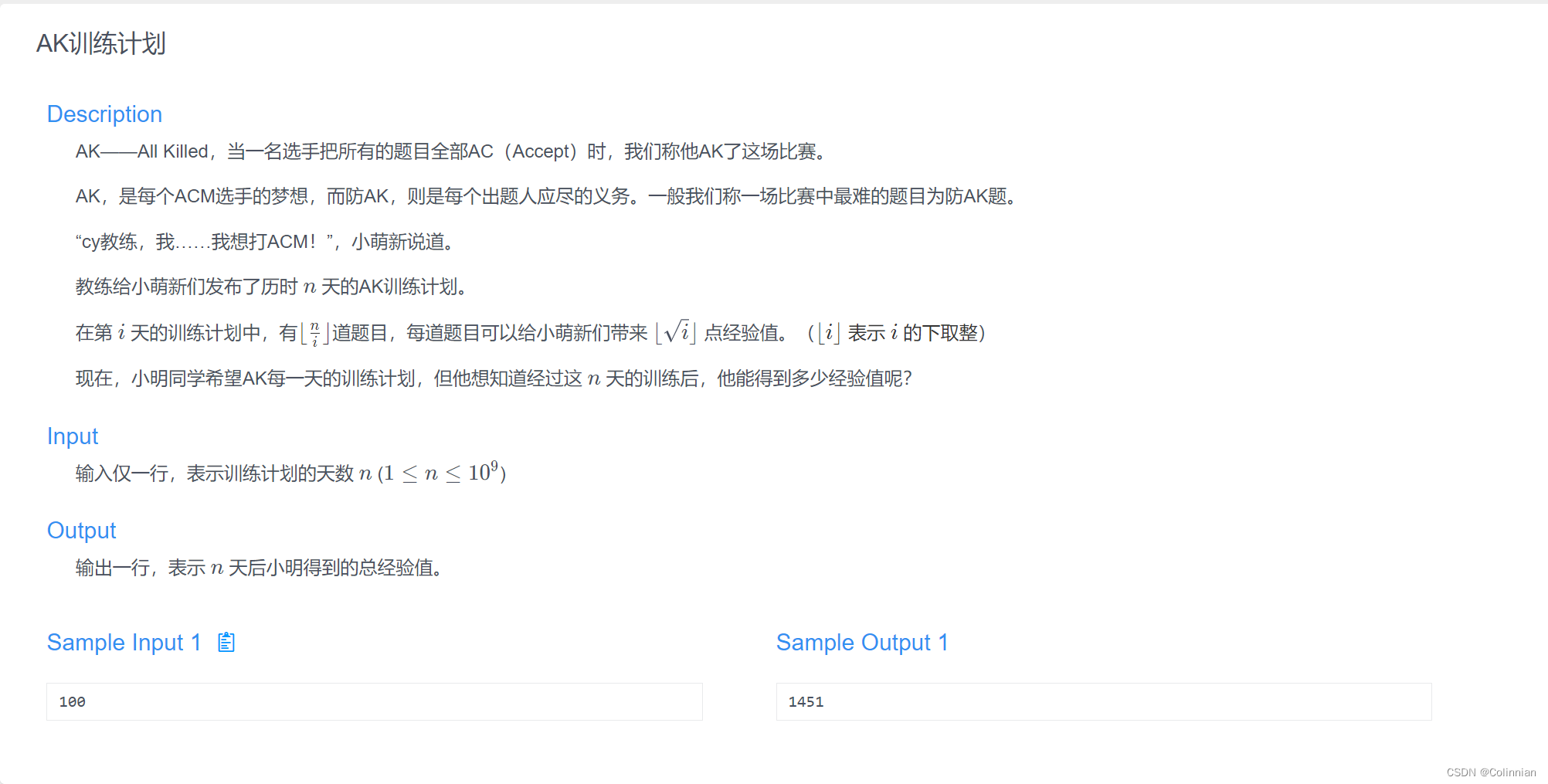 对于[sqrt(i)]也有块的性质,块的计算公式为r = ((ll)std::sqrt(l) + 1) * ((ll)std::sqrt(l) + 1);(ll是long long的意思,强制类型转换)
对于[sqrt(i)]也有块的性质,块的计算公式为r = ((ll)std::sqrt(l) + 1) * ((ll)std::sqrt(l) + 1);(ll是long long的意思,强制类型转换)
但是两个块的边界并不相同,所以可以考虑对边界取并集,使之成为一个新的分块,具体操作是取到两个块的所有边界,将边界进行排序.最后根据块的边界,两个数列分别对应的值求出答案
using ll = long long;
int main() {
std::ios::sync_with_stdio(false), std::cin.tie(0), std::cout.tie(0);
ll n, ans = 0;
std::cin >> n;
//取两个块的边界
ll l = 1, r = 0;
std::vector<int>k;
while (r < n) {
r = n / (n / l);
if(r<=n)k.push_back(r);
l = r + 1;
}
if (k.back() != n)k.push_back(n);
l = 1, r = 0;
while (r <= n) {
r = ((ll)std::sqrt(l) + 1) * ((ll)std::sqrt(l) + 1);
if (r <= n)k.push_back(r-1);
l = r + 1;
}
//k是新的块
ll m = k.size();
std::sort(k.begin(), k.end());
l = 0;
//根据新的块计算值
for (int i = 0; i < m; i++) {
r = k[i];
if (l == r)continue;
ll p = n / k[i], q = std::sqrt(k[i]);
ans = ans + p * q*(r-l);
l = r;
}
std::cout << ans;
return 0;
}



















 3429
3429

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








