【力扣】课程表

 🔥博客主页： 我要成为C++领域大神

🎥系列专栏：【C++核心编程】 【计算机网络】 【Linux编程】 【操作系统】

❤️感谢大家点赞👍收藏⭐评论✍️

本博客致力于分享知识，欢迎大家共同学习和交流。

你这个学期必须选修 numCourses 门课程，记为 0 到 numCourses - 1 。

在选修某些课程之前需要一些先修课程。 先修课程按数组 prerequisites 给出，其中 prerequisites[i] = [ai, bi] ，表示如果要学习课程 ai 则 必须 先学习课程  bi 。

例如，先修课程对 [0, 1] 表示：想要学习课程 0 ，你需要先完成课程 1 。
请你判断是否可能完成所有课程的学习？如果可以，返回 true ；否则，返回 false 。

示例 1：

输入：numCourses = 2, prerequisites = [[1,0]]
输出：true
解释：总共有 2 门课程。学习课程 1 之前，你需要完成课程 0 。这是可能的。
示例 2：

输入：numCourses = 2, prerequisites = [[1,0],[0,1]]
输出：false
解释：总共有 2 门课程。学习课程 1 之前，你需要先完成课程 0 ；并且学习课程 0 之前，你还应先完成课程 1 。这是不可能的

---

本题可以用拓扑排序，来判断是否能完成课程学习。但是题目没有直接告诉我们，课程之间的关系是一个图，那么我们应该如何得到这个信息呢？
在课程表问题中，通常给出了一组课程和它们之间的依赖关系，例如某些课程需要先修另一些课程才能学习。这种情况可以表示为有向图，其中课程是图中的顶点，依赖关系是图中的有向边。

判断一个课程表是否有效（即是否能够完成所有课程），可以通过拓扑排序来解决。拓扑排序可以判断有向图是否存在环，如果存在环，则无法完成所有课程，否则可以完成。

当题目中出现了这种强依赖关系时，我们首先考虑题目的情况是不是有向图。

为了更加直观的表示课程关系，我们可以将课程关系抽象为有向无环图。

 

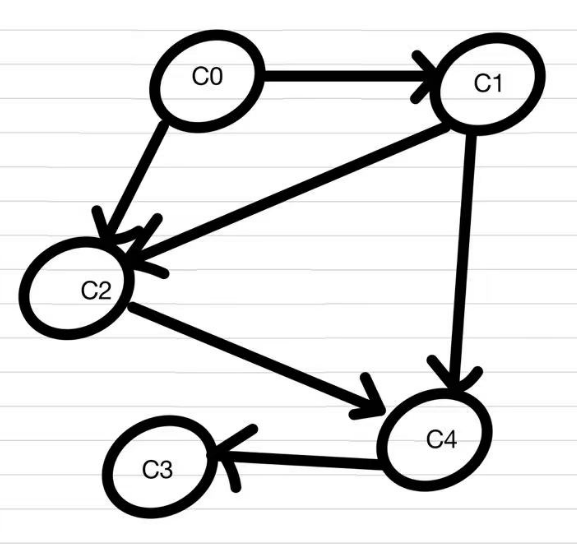
由图中可以看出，我们只能先学习入度为0的课程，即C0。学习C0课程，接着删除C0和它所指向的边。

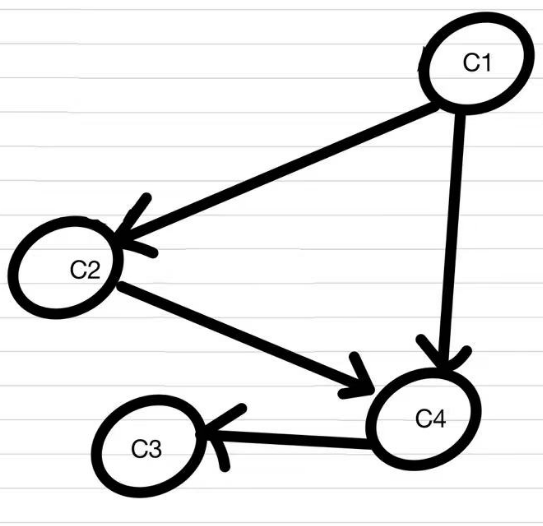
接着出现了新的入度为0的课程C1，重复上述步骤。

如果图的节点均可以被删除，则说明课程可以完成，反之不行。

流程

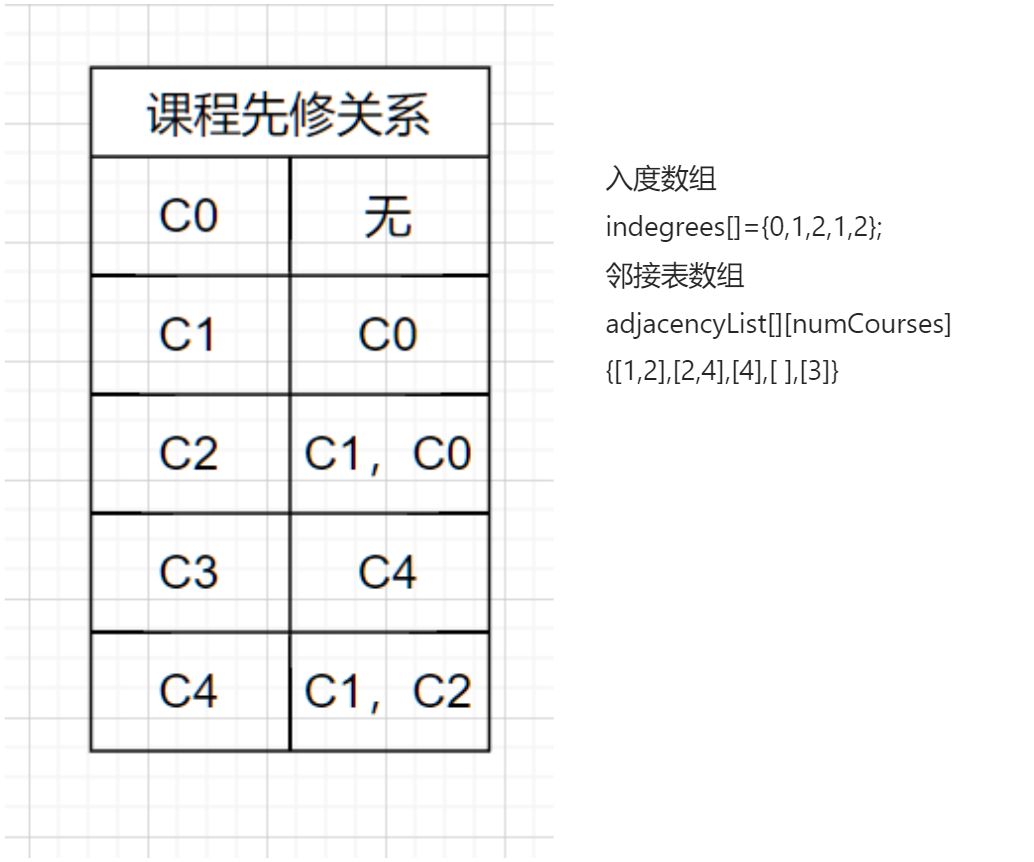
1.获得入度数组，和每个课程的邻接表（即后继课程）；
2.创建队列q，将所有入度为0的课程入队；
3.当队列q非空时，依次将队首节点进行出队，表示学习了这门课程，剩余课程数 numCourses--；

a.将该课程邻接表adjacencyList里的课程入度-1。

b.将新的入度为0的课程入队

4.返回 numCourses==0。

若整个课程安排图是有向无环图,则所有的节点一定都入队并出队过，即完成拓扑排序

因此，拓扑排序出队次数等于课程个数，返回numCourses==0判断课程是否可以成功安排

 

代码实现：

💡 Tips：拓扑排序

class Solution {
public:
    bool canFinish(int numCourses, vector<vector<int>>& prerequisites) {
    vector<int> indegrees(numCourses, 0);
    vector<vector<int>> adjacencyList(numCourses, vector<int>());
    queue<int> q;

    //获得入度数组 和 每个课程的邻接表
    for(auto &prerequisite:prerequisites)
    {
        indegrees[prerequisite[0]]+=1;
        adjacencyList[prerequisite[1]].push_back(prerequisite[0]);
    }

    //将入度为0 的课程入队
    for(int i=0;i<numCourses;++i)
    {
        if(indegrees[i]==0)
        {
            q.push(i);
        }
    }

    //处理操作
    while(!q.empty())
    {
        int course=q.front();
        q.pop();
        numCourses--;
        for(int successor :adjacencyList[course])
        {
            if(--indegrees[successor]==0) q.push(successor);
        }
    }

    return numCourses==0;
    }
};

类似题目

210. 课程表 II
只需在入度为0的课程出队的同时，将该课程添加到返回数组中。