文章讲述了作者参加的一场编程竞赛，涉及四个题目：爬楼梯、字符折线图、吉利数和路灯照明。作者详细解释了每个题目的解题思路和AC代码，展示了比赛过程中的思考和策略。
日期：2023.10.1
学号：S09235
一：
总分数：
T1【爬楼梯（stair）】：100
T2【字符折线图（sline）】：40
T3【吉利数（lucknum）】：0
T4【路灯照明（lighting）】：0
二、比赛过程
第一题比较简单，但需理解透了才能得分，因为与要注意：小可记录的是每一步迈出去的距离能够跨越多少个台阶，比如还剩一个台阶就能到达下一个平台，小可步子迈的再大，也只能上一个台阶（也就是说，小可不能跨平台），所以，只要注意这一点，并写出关键代码，就能得分。
第二题是仅次于第四题的难题，因为需要注意换行、上升下降的位置以及“\”的输出方法（正确输出是：cout<<"\\";），这个题实际是可以偷分的，因为全是上和全是下以及全是平的是可以轻松判断，上下平波动的我没有想到，故只得了40分。
第三题是仅次于第一题的难题，开始我想用枚举骗分，但是枚举完后程序运行不了，所以没得分。
第四题是最难的题（堪称“难题中的难题”），一开始读到题面，我以为考到了，我刚学一点的贪心，但后来觉得小学组不大可能上D4难度，于是想到了二分答案（最小化答案），但是呢，写不出代码，故强制输出，没得分。
三、比赛分析
T1【爬楼梯（stair）】
1、题目大意
小可爬楼梯，两个平台对应一层楼，x个楼梯对应一个平台，小可要N步才能走完x个台阶，有N个数，代表一次上ai个台阶，求小可上了几层。
2、比赛中的思考
这个题其实就是一个K1的顺序结构，没啥好说的。
3、解题思路
说下大概步骤：
（1）累加步数（边输入边做）
（2）当累加值>x时，则累加器清空，平台数+1
（3）最后平台数/2得到楼层数
4、AC代码
我废话不多说，不多说废话，说废话真得很烦，所以我从不说废话，上AC代码：
#include<bits/stdc++.h>
#define ll long long
using namespace std;
int n,x,tmp,sum,cnt;
int main(){
scanf("%d%d",&n,&x);
for(int i=1;i<=n;i++){
scanf("%d",&tmp);
if(sum+tmp>=x){
sum=0;
cnt++;
}
else sum+=tmp;
}
printf("%d\n",1+int(cnt/2));
return 0;
}
T2【字符折线图（sline）】
1、题目大意
我们根据一个字符串，可以画出一个折线图，从第二个字符开始，如果它比它的上一个字符大，那么就是上升的，画一个 / ；如果和上一个字符相同，那么画一个 - ；如果比比上一个字符小，那么就是下降的，画一个 \ 。并且上升的时候，要向上一行，下降的时候向下一行。
如例子：
2、比赛中的思考
这个题我当时没打算拿全分的，打算拿只有一行的输出的，故对了8个样例，拿了40分。其实那40分很简单，只需要不注意空格、换行，按照题目要求即可。
3、解题思路
pre的作用：是上一个数据，帮助我们找到下一个数据的位置
if(pre==2) line++; if(pre==3) line--;
//判断：等于2要上升，高度++
等于3要下降，高度--
if(pre!=3) line++;
//判断：不是3，就是2，则上升，高度++
if(pre!=2) line--;
//判断：不是2，就是3，则下降，，高度--
4、AC代码
好，我废话不多说，不多说废话，因为说废话真的很烦，也不知道大家喜不喜欢话说废话，不过我是从不说废话的，那我们上AC代码：
#include<bits/stdc++.h>
using namespace std;
int a[405][405],pre,line=200;
int main(){
string s;
cin>>s;
for(int i=1;i<s.size();i++){
if(s[i]==s[i-1]){
if(pre==2) line++;
if(pre==3) line--;
a[line][i]=pre=1;
}
else if(s[i]>s[i-1]){
if(pre!=3) line++;
a[line][i]=pre=2;
}
else{
if(pre!=2) line--;
a[line][i]=pre=3;
}
}
for(int i=0;i<400;i++){
for(int j=200;j>0;j--){
if(a[i][j]){
a[i][0]=j;
break;
}
}
}
int st=400,en=0;
while(a[st][0]==0) st--;
while(a[en][0]==0) en++;
for(int i=st;i>=en;i--){
for(int j=1;j<=a[i][0];j++){
if(a[i][j]==1) cout<<"-";
else if(a[i][j]==2) cout<<"/";
else if(a[i][j]==3) cout<<"\\";
else cout<<" ";
}
cout<<endl;
}
return 0;
}
T3【吉利数（lucknum）】
1、题目大意
小可认为一个数字中如果有 这个数字就是不吉利的。相对的，其他的数字就是吉利的。吉利的数字有 1,2,3,5,6,7,8,9,10,..
小可想知道，第n个吉利的数字是多少。
2、比赛中的思考
没啥好说的，就是枚举骗分，但我后来枚举运行不了，就没拿到分
3、解题思路
60分思路
直接进行暴力枚举即可。从 开始枚举，碰到吉利数，计数器加一。当计数器等于 时，输出结果。时间复杂度
80分思路
先进行打表预处理，记录前 个吉利数都是谁，当输入询问的时候直接输出即可。这样就可以应对的范围最大到 ，但是询问次数到 的情况。时间复杂度
O(n + T)
100分思路
将十进制转换为九进制，对于数字中大于等于 的位置，加一输出即可。
因为相当于在十进制中，去掉了 这个数字，那么就是九进制。
九进制中的 对应十进制中的 ，
九进制中的 对应十进制中的 ，
九进制中的 对应十进制中的 ，
九进制中的 对应十进制中的 ，
九进制中的 对应十进制中的 ，
九进制中的 对应十进制中的 ，
九进制中的 对应十进制中的 ，
九进制中的 对应十进制中的 ，
九进制中的 对应十进制中的 ，
九进制中没有九这个数字。
正好一一对应。
时间复杂度
O(Tlogn)
4、AC代码
上AC代码：
#include<bits/stdc++.h>
using namespace std;
string s;
long long a[105],n,cnt;
int main(){
int t;
cin>>t;
while(t--){
scanf("%lld",&n);
cnt=0;
while(n){
a[cnt]=n%9;
n/=9;
cnt++;
}
for(int i=cnt-1;i>=0;i--){
if(a[i]<4) cout<<a[i];
else cout<<a[i]+1;
}
printf("\n");
}
return 0;
}
T4【路灯照明（lighting）】
1、题目大意
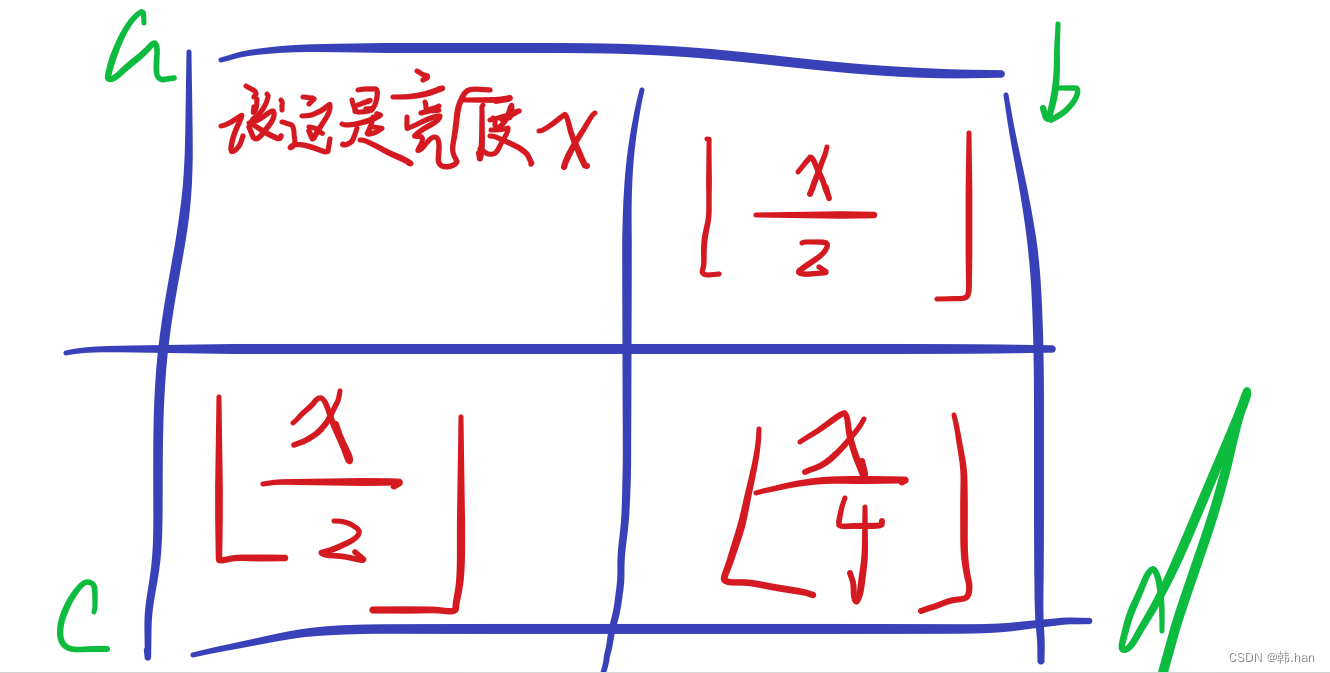
2、比赛中的思考
我画了好几个图，但写不出代码，然后...就没有然后了，得了0分
3、解题思路
本题显然具有二分性，考虑二分答案。
假设总共有 的耗电量可以分配给四盏灯，我们考虑如何分配：
枚举对角线的两盏灯的耗电量，假设枚举的是 左上角 和右下角 。那么我们可以发现，右上角这个格子当前亮度为 ⌊a/2+b/2⌋，左下角的格子的亮度也一样。我们可以算出这两个格子的亮度与需求的差值，再将mid − a − b的耗电量分配给这两盏灯。
一种减少写代码细节的小技巧是：算出左下角格子的大致耗电量，然后用for循环在估计值的附近枚举即可，这样就不需要判断边界条件了。
4、AC代码
#include <algorithm>
#include <cmath>
#include <cstdio>
#include <cstring>
#include <ext/pb_ds/assoc_container.hpp>
#include <ext/pb_ds/tree_policy.hpp>
#include <ext/rope>
#include <iostream>
#include <map>
#include <queue>
#include <random>
#include <set>
#include <stack>
#include <vector>
#define CLOSE ios::sync_with_stdio(false), cin.tie(0), cout.tie(0);
#define isd(c) ('0' <= (c) && (c) <= '9')
#define isa(c) ('a' <= (c) && (c) <= 'z')
#define isA(c) ('A' <= (c) && (c) <= 'Z')
#define mem(a, b) memset(a, b, sizeof a);
#define N 100005
#define M 2000005
#define mod 1000000007
#define inf 0x3f3f3f3f
#define infll 0x3f3f3f3f3f3f3f3f
#define ll long long
#define ull unsigned long long
#define PI acos(-1)
#define endl "\n"
#define pii pair<int, int>
#define F first
#define S second
#define bug cout << endl << " .....here!...." << endl;
//#pragma GCC optimize("O3")
using namespace std;
using namespace __gnu_cxx;
using namespace __gnu_pbds;
int a, b, c, d;
bool check(int mid)
{
for (int i = 0; i <= a; i++)
{
for (int j = 0; j <= d; j++)
{
int need = max(a - i - j / 4, d - j - i / 4);
if ((mid - i - j) / 2 < need)
continue;
int now = mid - i - j;
int bneed = max(0, b - i / 2 - j / 2);
int cneed = max(0, c - i / 2 - j / 2);
int bb = max(0, (bneed - now / 4) * 4 / 3);
for (int k = max(0, bb - 5); k <= min(now, bb + 5); k++)
if (k + (now - k) / 4 >= bneed && k / 4 + now - k >= cneed)
return true;
}
}
return false;
}
int main()
{
CLOSE
cin >> a >> b >> c >> d;
int l = 0, r = a + b + c + d, ans = a + b + c + d;
while (l <= r)
{
int mid = (l + r) >> 1;
if (check(mid))
{
ans = mid;
r = mid - 1;
}
else
l = mid + 1;
}
cout << ans << endl;
}
扫一扫
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
