常见的几种距离

        在机器学习、数据挖掘等领域，常用的距离主要有欧氏距离、曼哈顿距离、切比雪夫距离、余弦距离四种，它们的计算逻辑和适用场景差异明显，核心是解决 “如何衡量两个数据点（或向量）的相似性 / 差异性” 的问题。

1. 欧氏距离（Euclidean Distance）

定义：在n维空间中，两点之间的直线距离。

公式：对于两点 A(x1​,x2​,...,xn​) 和 B(y1​,y2​,...,yn​)，欧氏距离为：

        如：A(0,0),B(3,4)，AB之间的欧式距离为(3^2+4^2)^(1/2)=5

适用场景：

        需衡量 “绝对空间距离” 的场景，如 K-Means 聚类、K-NN 分类。

2. 曼哈顿距离（Manhattan Distance）

        曼哈顿距离又称 “城市街区距离”，模拟在网格中沿坐标轴移动的总距离。

定义：两点在各维度上的坐标差的绝对值之和，是闵可夫斯基距离当 p=1 时的特殊情况。

公式：对于两点 A(x1​,x2​,...,xn​) 和 B(y1​,y2​,...,yn​)，曼哈顿距离为：

        A(0,0),B(3,4)，AB之间的曼哈顿距离为|3-0|+|4-0|=7

适用场景：

        需忽略 “对角线捷径”、关注 “各维度累计差异” 的场景，如 L1 正则化（防止过拟合）。

        实际问题中的路径计算，如出租车在城市道路中的行驶距离、物流配送的路线长度。

3. 切比雪夫距离（Chebyshev Distance）

 定义：两点在所有维度上坐标差的最大值，是闵可夫斯基距离当 p→∞时的极限情况。

公式：对于两点 A(x1​,x2​,...,xn​) 和 B(y1​,y2​,...,yn​)，切比雪夫距离为：

       如： A(3,4,5),B(6,8,10)，AB之间的切比雪夫距离为：5

        |6-3|=3，|8-4|=4，|10-5|=5

适用场景:

        需关注 “最显著差异维度” 的场景，如多指标评价（如产品质量检测，只要某一项指标不达标即判定不合格）。

        棋盘游戏、机器人路径规划（如机器人需同时调整 x、y 方向位置，最大移动步长由差异最大的方向决定）。

4. 余弦距离（Cosine Distance）

        衡量 “向量方向的相似性”，而非 “空间位置的远近”，本质是基于余弦相似度推导。

定义：通过计算两个向量的夹角余弦值，再用 1 减去余弦相似度得到（余弦相似度越接近 1，余弦距离越接近 0，向量方向越一致）。

公式：对于两个向量 a(x1​,x2​,...,xn​) 和 b(y1​,y2​,...,yn​)，余弦距离为：

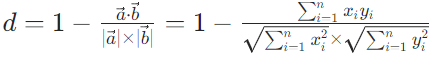
        如：A=(8,2)，B=(4,1)

        1.计算点积：A⋅B=(8×4)+(2×1)=32+2=34

        2.计算向量模长：

                ∣A∣=82+22​=64+4​=68​≈8.246

                ∣B∣=42+12​=16+1​=17​≈4.123

        3.计算余弦相似度：

        4.计算余弦距离：d=1−cosθ=1−1=0

适用场景：

        需忽略 “向量长度（量级）”、仅关注 “方向” 的场景，如文本相似度计算（用 TF-IDF 向量表示文本，不关心文本长度，只关心主题是否一致）。

        图像特征匹配、推荐系统（如推荐 “兴趣方向相似” 的用户，不考虑用户活跃度的高低）。