二分算法详解

最新推荐文章于 2025-11-24 15:27:16 发布

原创最新推荐文章于 2025-11-24 15:27:16 发布 · 539 阅读

10 ·

CC 4.0 BY-SA版权

文章标签：

#算法 #c++

算法专栏收录该内容

3 篇文章

订阅专栏

一、二分算法的思想

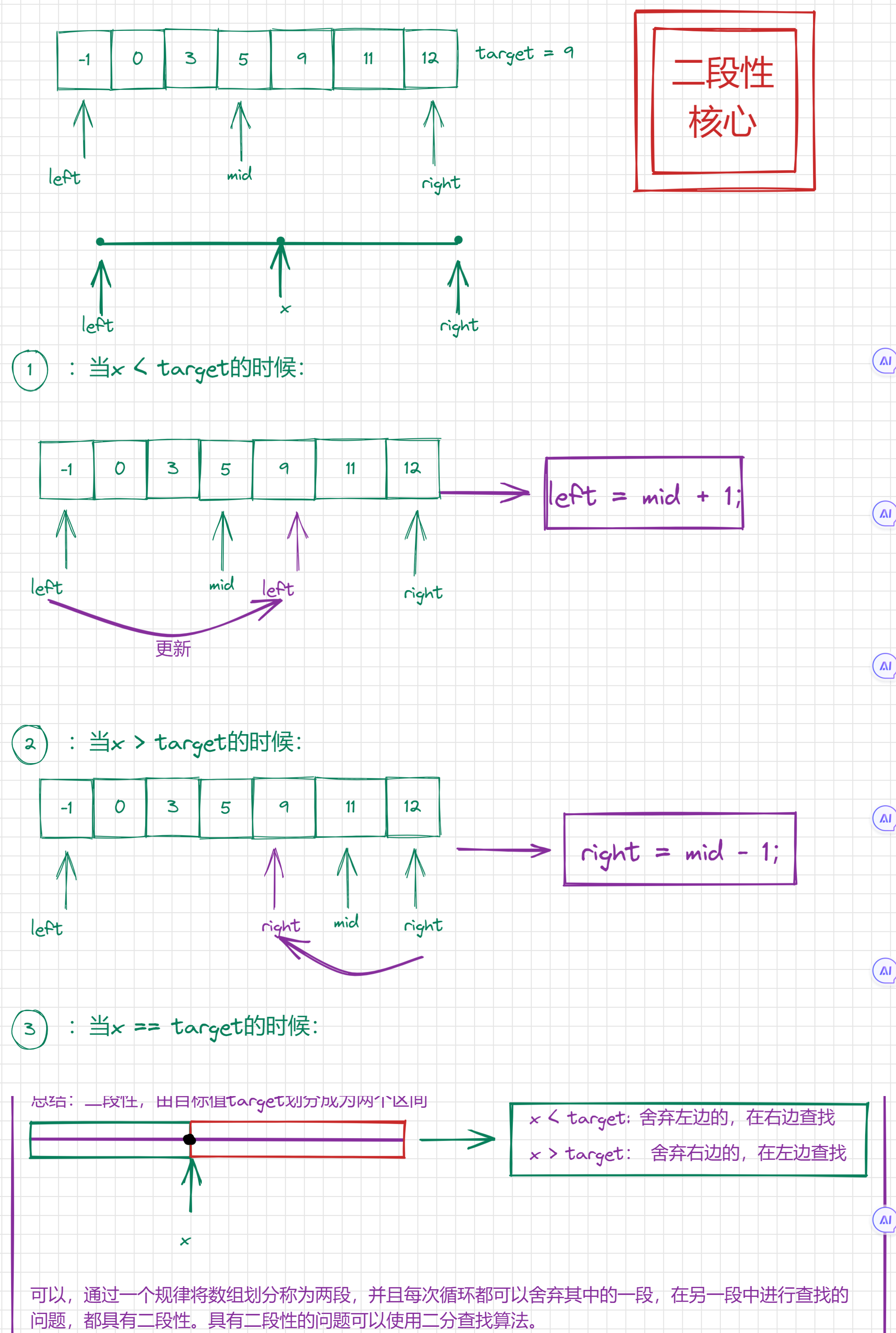
二分算法的思想是为了加快查找的效率而诞生的，具体如何使用二分查找算法，在于如何去发现题目中的二段性，当我们找到二段性后，就可以直接摒弃其中的一段区间，去另一端区间中查找，进而提高查询的效率。

二、朴素的二分算法

通过下面这道题目来进行总结朴素的二分模板

题目分析：在数组nums中查找一个指定值target。

2.1、暴力解法解决问题

解法一：暴力解法

2.2、二分算法进行优化

2.2.1、总体思想

解法二：二分算法优化

有什么算法可以实现同样的功能但是时间复杂度可以更低呢？
我们可以发现我们是将所有的元素都和目标值进行比较那么有没有什么方法可以少比较几次呢？其实是有的，我们可以发现数组是有序的，那么我们可以利用数组有序这个特点(单调性)来进行优化。

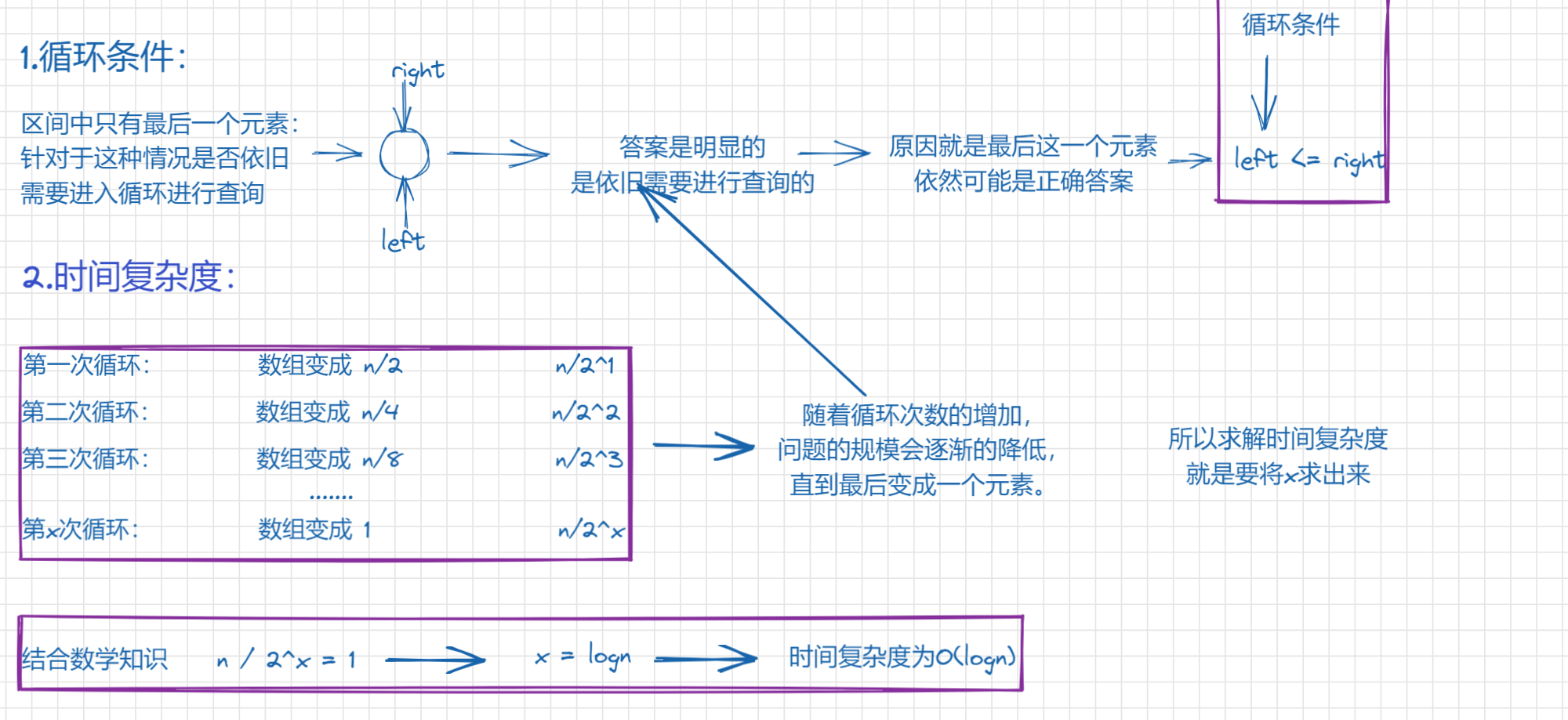
2.2.2、二分算法的细节

2.2.3、可以使用朴素二分来解决的问题

针对于什么样的题目适合使用二分算法来解决这个问题，之前已经记录过了。就是如果这个问题是具有二段性的就可以使用二分算法来解决。

这里要进行一下声明：就是并不是大家公认的只有数组具有单调性才可以使用二分算法，数组具有单调性只是二段性的一种体现，并不能说单调性就是二段性，或者二段性就是单调性。

2.2.4、问题的代码和模板

解决问题的答案代码:

class Solution {
public:
    int search(vector<int>& nums, int target) {
        int left = 0, right = nums.size() - 1;
        while (left <= right)
        {
            int mid = left + (right - left) / 2;
            if (nums[mid] < target) left = mid + 1;
            else if (nums[mid] > target) right = mid - 1;
            else return mid;
        }
        return -1;
    }
};

下面是总结的模板：

int left = 0, right = nums.size() - 1;
        while (left <= right)
        {
            int mid = left + (right - left) / 2;
            if (// 结合二段性) left = mid + 1;
            else if (// 结合二段性) right = mid - 1;
            else return // 结合二段性;
        }
        return -1;

三、二分左右端点的模板

3.1、二分左右端点的引入

上面的题目总结出的是朴素的二分模板，在解决问题时有很大的局限性，下面再来介绍两种模板，就可以解决二分问题中的大多数问题了。

3.2、二分左右端点的题目

通过下面这道题目来总结一下二分左右端点的模板。

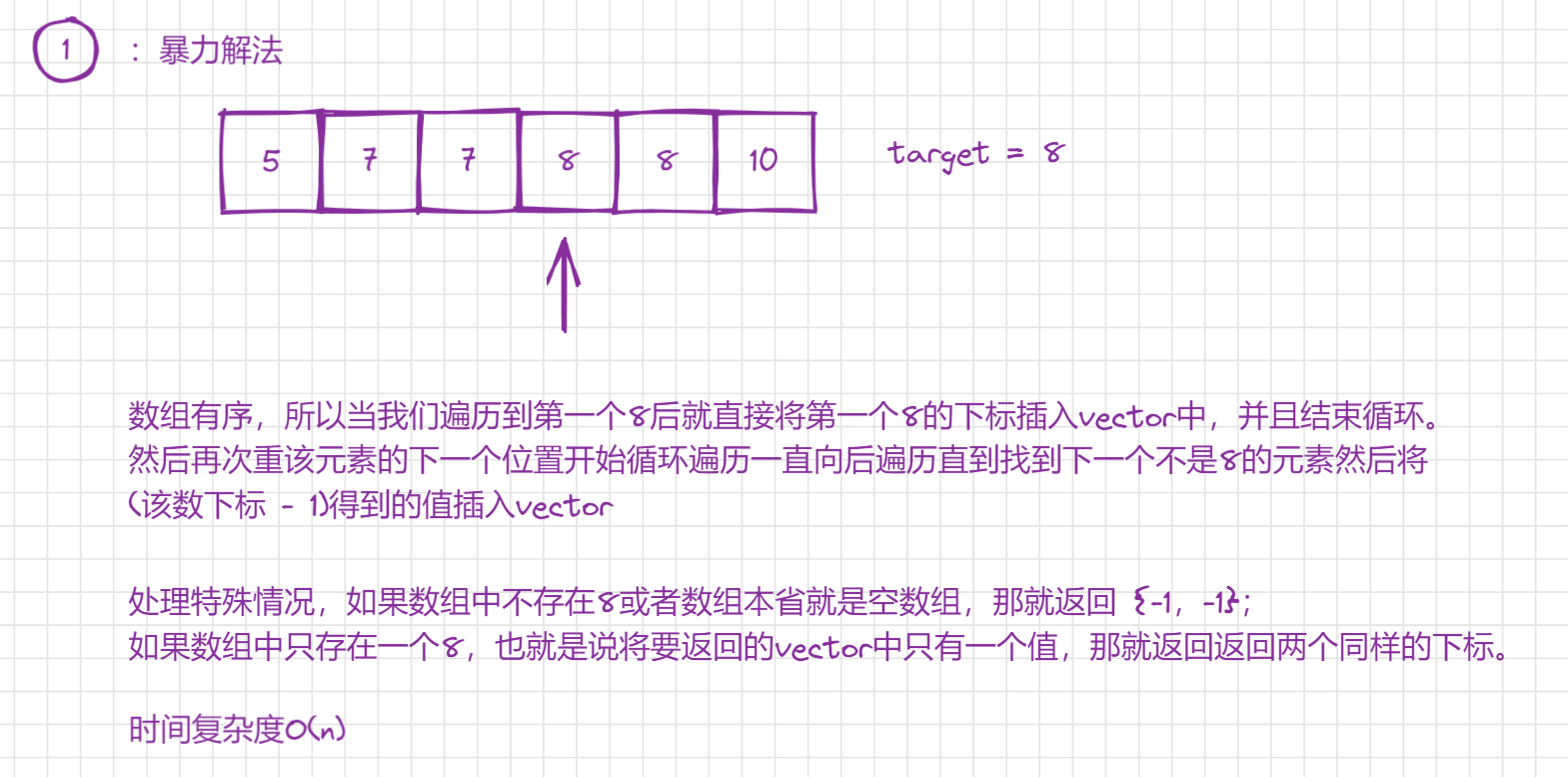
题目分析：题目要求我们返回一个数组中的target元素的开始下标和结束下标。如果没有这个元素或者数组为空就返回{-1， -1}；

3.2.1、暴力解法解决问题

解法一：暴力解法

3.2.2、二分算法进行优化

解法二：二分算法

3.2.2.1、二分左端点

3.2.2.1.1、总体思想

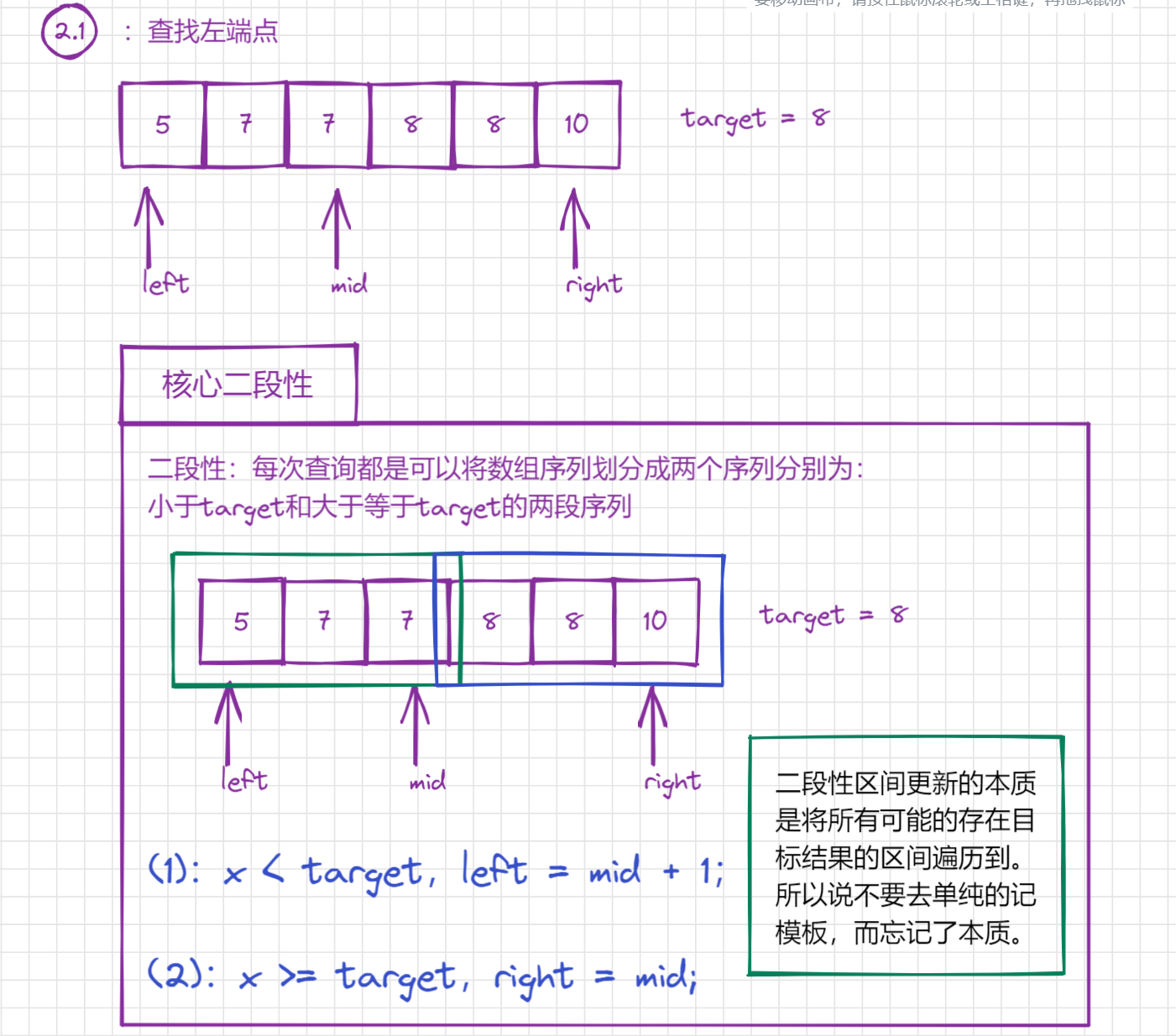
3.2.2.1.2、细节问题

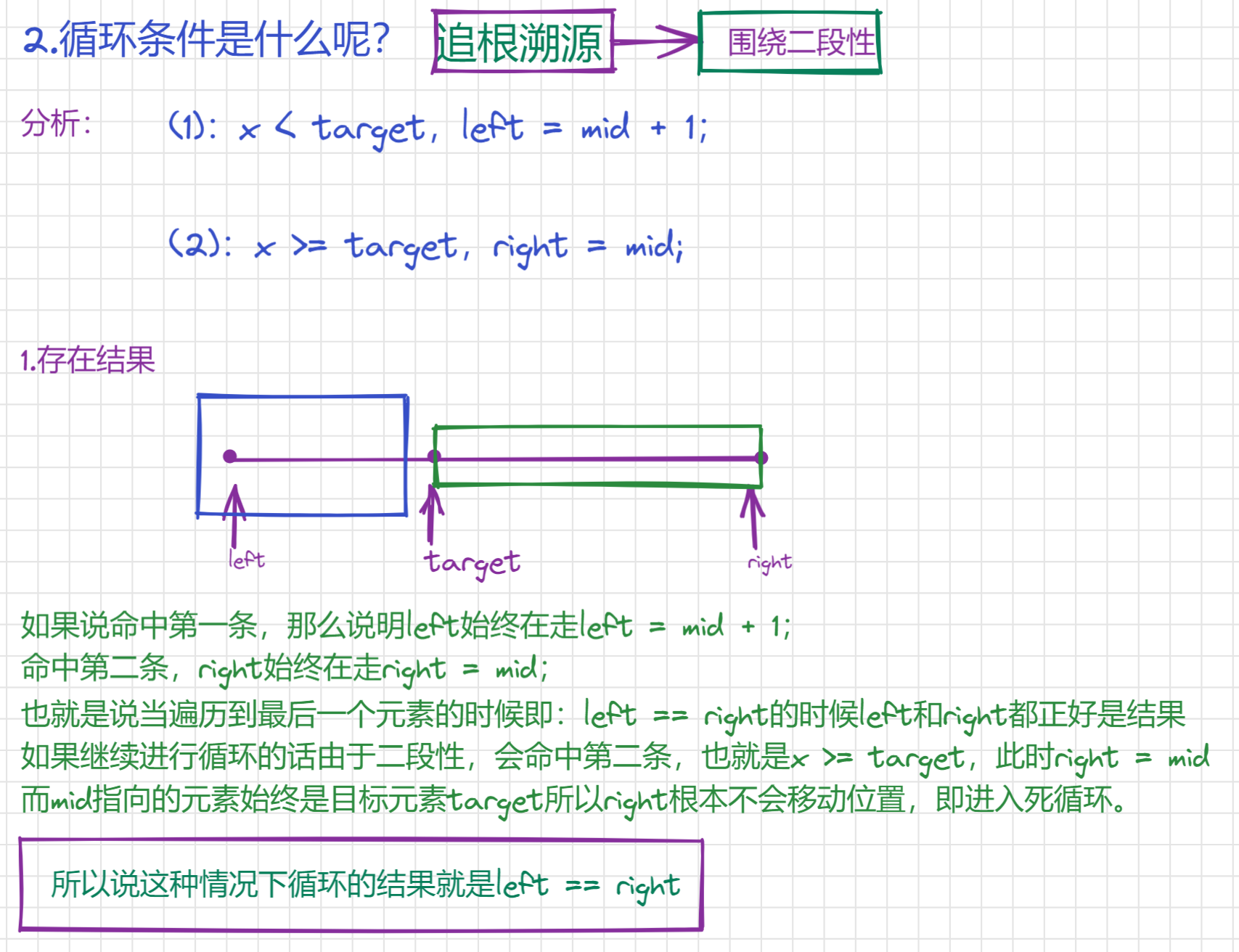
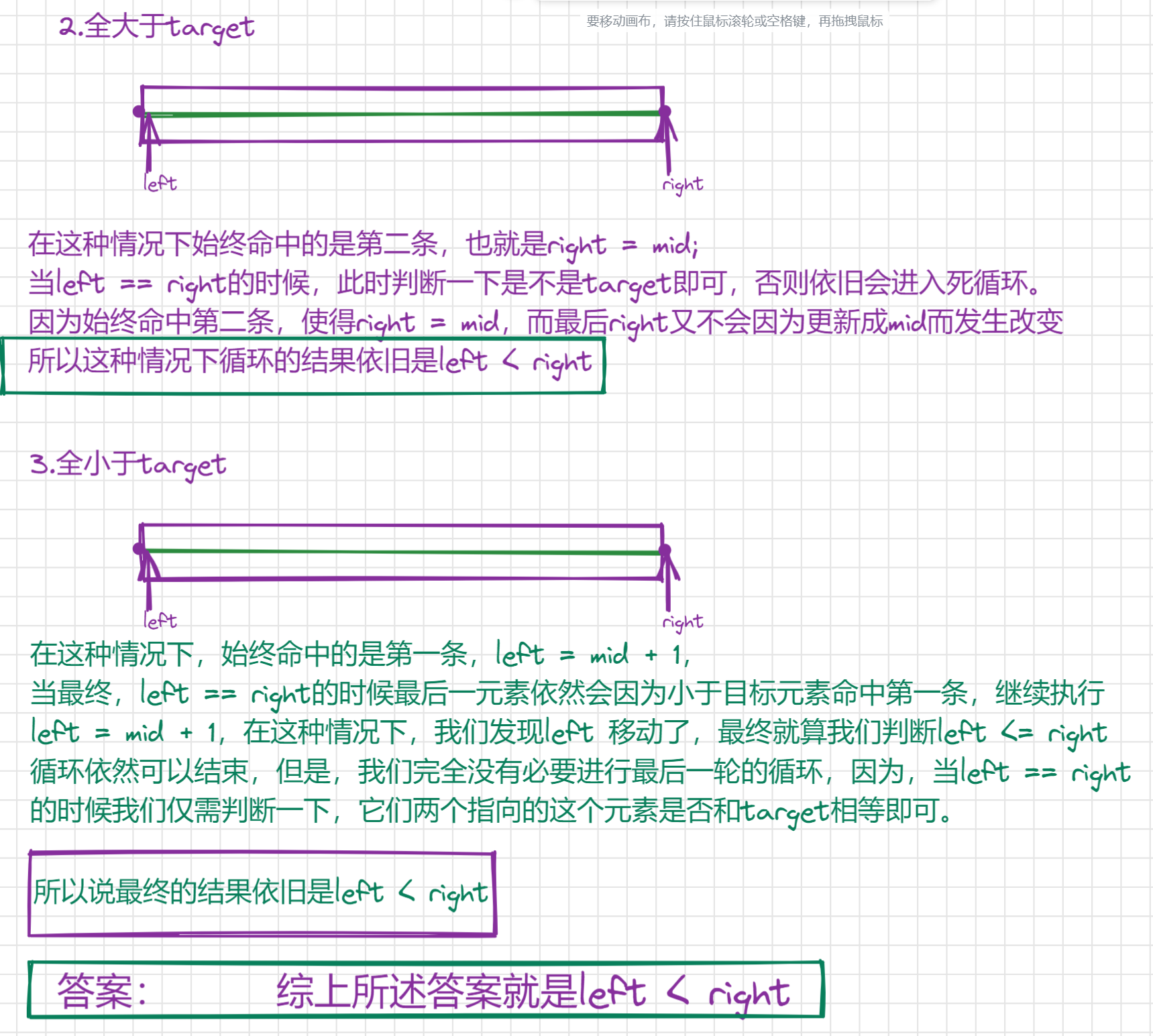
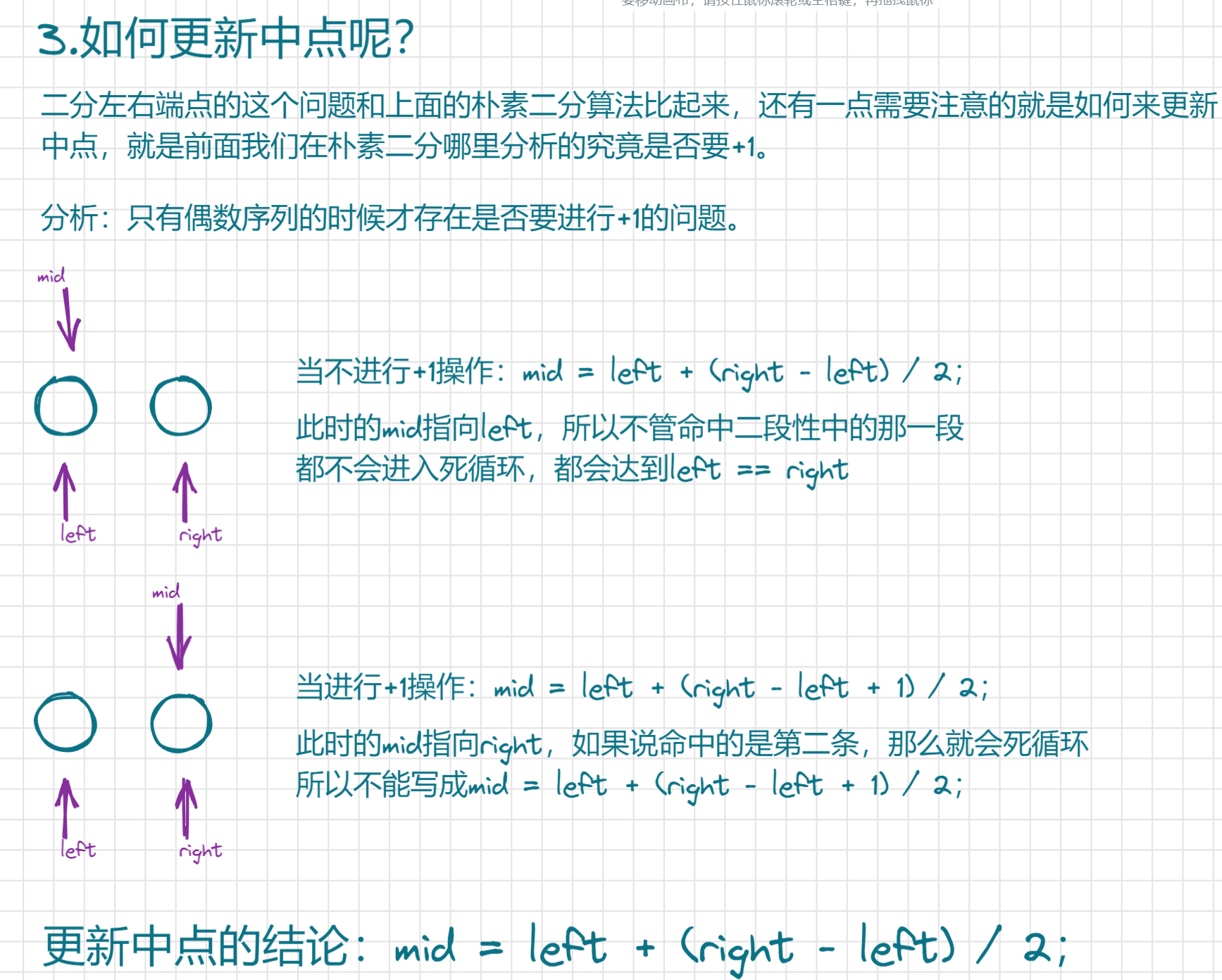
3.2.2.1、二分右端点

3.2.2.1.1、总体思想

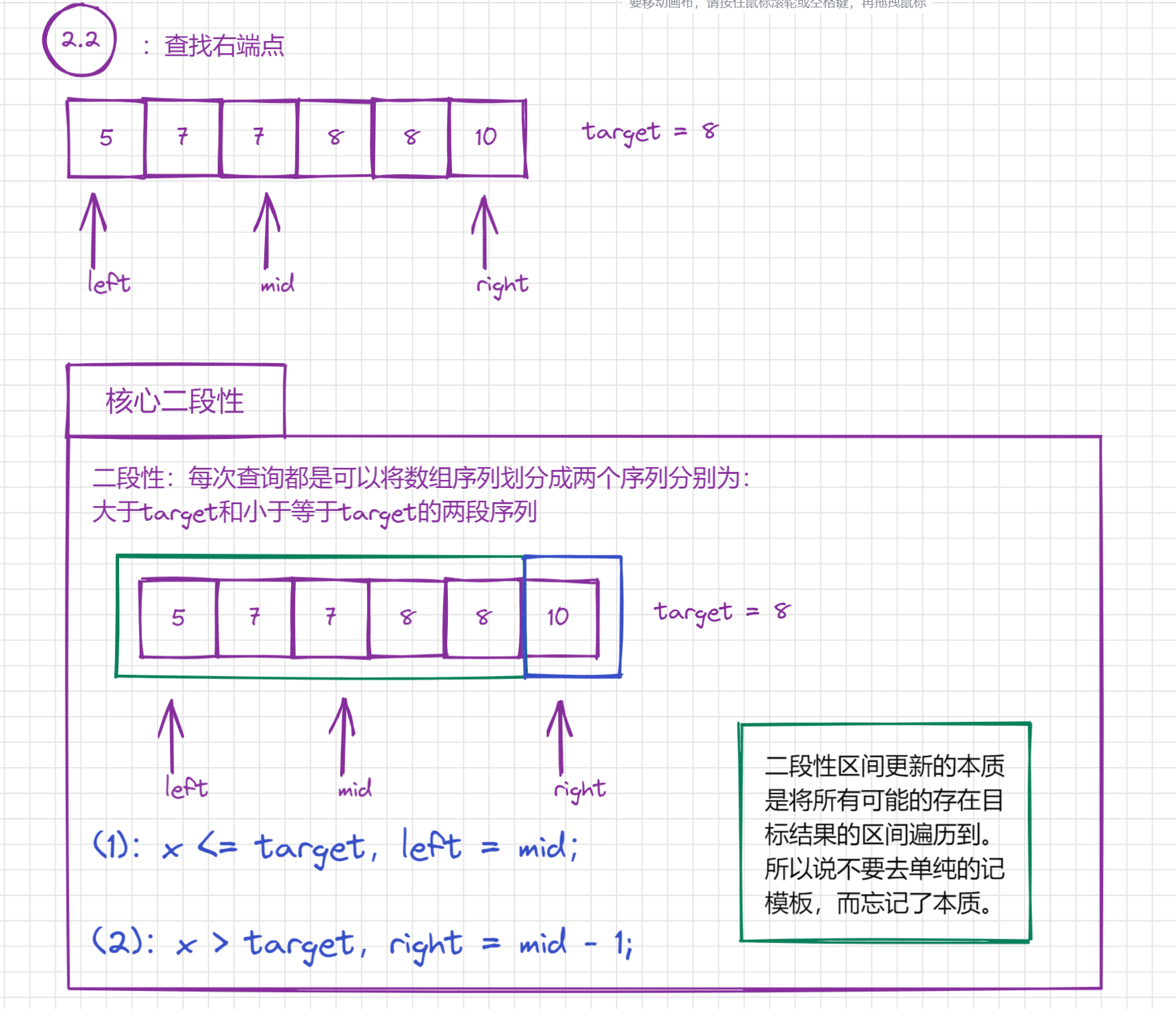
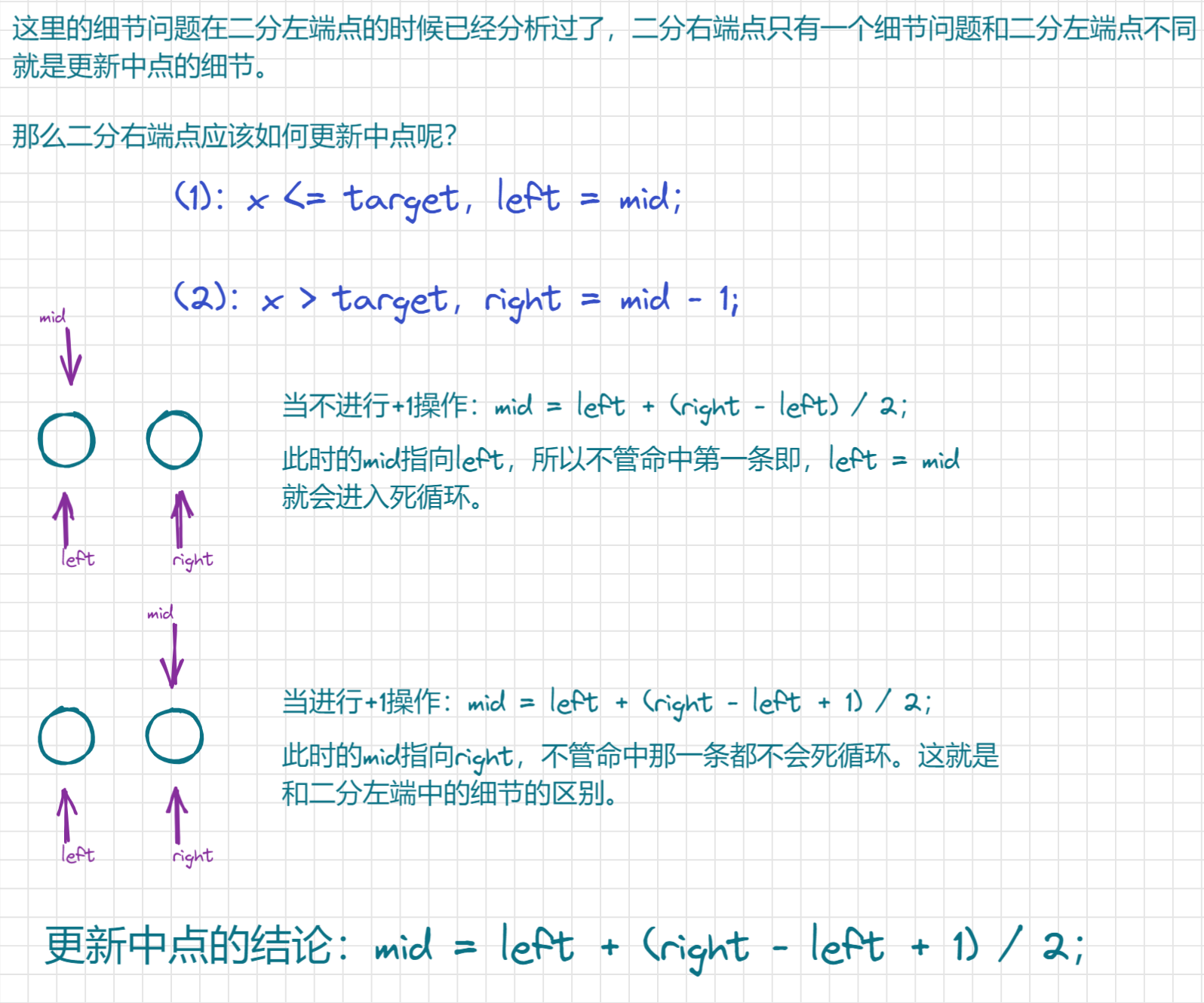
3.2.2.1.2、细节问题

3.2.3、代码即模板

答案代码：

class Solution {
public:
    vector<int> searchRange(vector<int>& nums, int target) 
    {
        // 判断临界情况
        if (nums.size() == 0) return {-1, -1};
        // 1.二分左端点
        int begin = -1; // 记录左端点
        int left = 0, right = nums.size() - 1;
        while (left < right)
        {
            // 注意取中点
            int mid = left + (right - left) / 2;
            // 二段性
            if (nums[mid] < target) left = mid + 1;
            else right = mid;
        }
        // 因为数组中可能不含有target,所以进行一下判断
        if (nums[left] == target) begin = left;

        // 2.二分右端点
        left = 0, right = nums.size() - 1;
        while (left < right)
        {
            // 注意取中点
            int mid = left + (right - left + 1) / 2;
            // 二段性
            if (nums[mid] > target) right = mid - 1;
            else left = mid;
        }
        if (nums[left] != target) return {begin, -1};
        return {begin, left};
    }
};

二分左右端点的模板：

        // 1.二分左端点
        int begin = -1; // 记录左端点
        int left = 0, right = nums.size() - 1;
        while (left < right)
        {
            // 注意取中点
            int mid = left + (right - left) / 2;
            // 二段性
            if (// 结合二段性) left = mid + 1;
            else right = mid;
        }
        // 因为数组中可能不含有target,所以进行一下判断
        if (nums[left] == target) begin = left;


        // 2.二分右端点
        left = 0, right = nums.size() - 1;
        while (left < right)
        {
            // 注意取中点
            int mid = left + (right - left + 1) / 2;
            // 二段性
            if (// 结合二段性) right = mid - 1;
            else left = mid;
        }
        if (nums[left] != target) return {begin, -1};

记住两个模板的关键，就记住如何取中点就可以了，因为二段性是需要我们结合题目去判断的，即如果我们判断出的二段性是有-1的操作的就是二分右端点，更新中点时就是要+1，否则就是二分左端点，更新中点时就不需+1。