【动态规划】[NOIP2002 普及组] 过河卒

[NOIP2002 普及组] 过河卒

题目描述

棋盘上 $A$ 点有一个过河卒，需要走到目标 $B$ 点。卒行走的规则：可以向下、或者向右。同时在棋盘上 $C$ 点有一个对方的马，该马所在的点和所有跳跃一步可达的点称为对方马的控制点。因此称之为“马拦过河卒”。

棋盘用坐标表示，$A$ 点 $(0,0)$、$B$ 点 $(n,m)$，同样马的位置坐标是需要给出的。

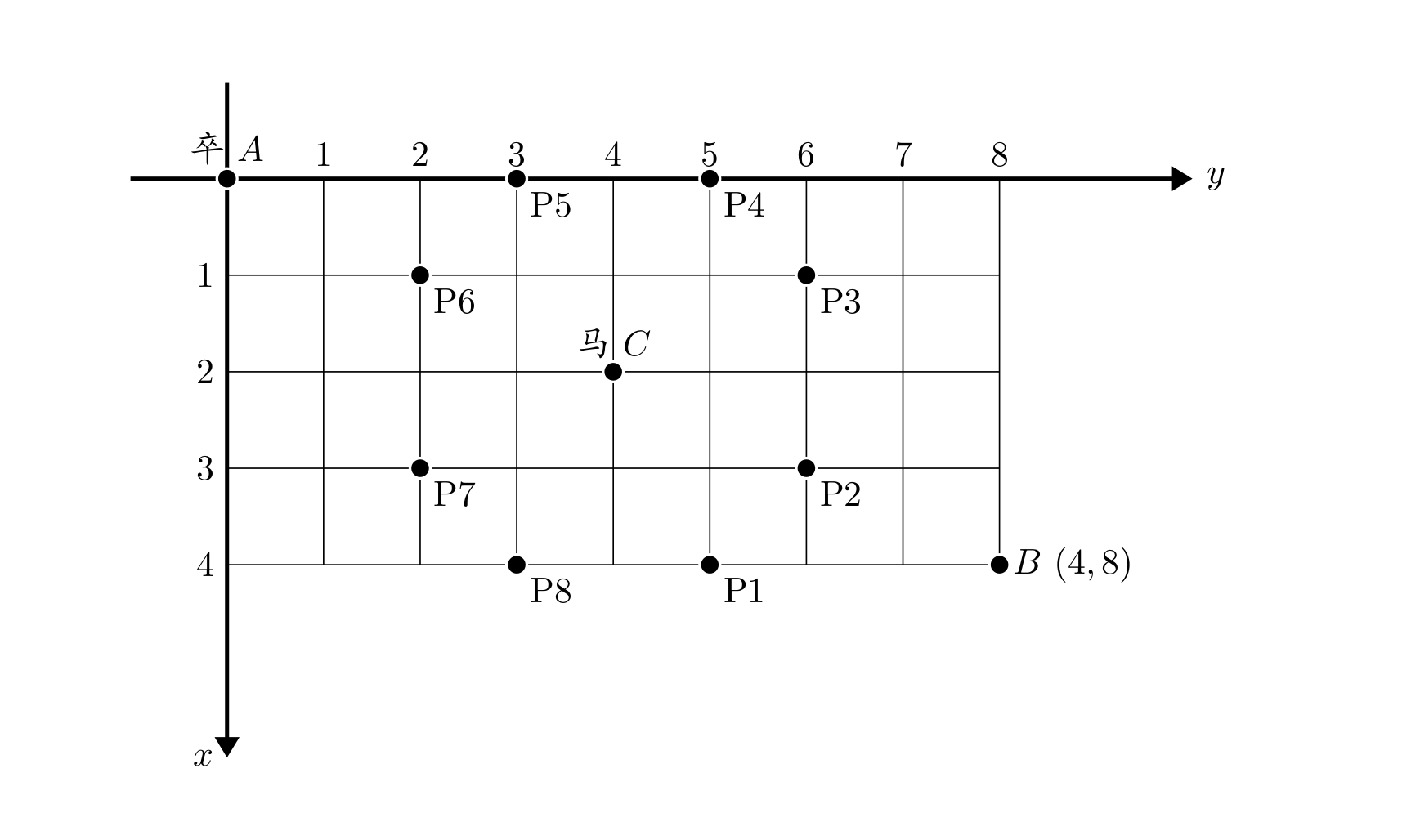
现在要求你计算出卒从 $A$ 点能够到达 $B$ 点的路径的条数，假设马的位置是固定不动的，并不是卒走一步马走一步。

输入格式

一行四个正整数，分别表示 $B$ 点坐标和马的坐标。

输出格式

一个整数，表示所有的路径条数。

分析

显然，这道题可以使用动态规划解决，卒的移动是一个多阶段问题，只要每一次移动都不会被马吃掉，那么这条路径就是可行的
解决动态规划问题使用了递推的思想，当前的状态可以用之前的状态推出
首先我们要使用一个dp数组作为递推数组

第一步：确定递推数组的含义

由于棋子在棋盘上的移动是二维的，我们用一个二维数组dp[][]来存储结果
dp[i][j]就表示卒从(0, 0)点移动到(i, j)点所有路径的条数

第二步：找出数组元素之间的递推关系式

依题意，卒每次只能向下或向右移动一个单位长度，当前棋子坐标为(i, j)时，棋子只可能从(i - 1, j)向下移动一格来到(i, j)，或者从(i, j - 1)向右移动一格来到(i, j)
因此我们可以得到递推公式：
dp[i][j] = dp[i - 1][j] + dp[i][j - 1]

第三步：找出初始值或边界条件

如果在上边界上，那么当前位置只能是从前一个位置向右移动得到的；同理，如果在左边界上，那么当前位置只能是从上一个位置向下移动得到的
则有如下递推关系：
dp[0][j] = dp[0][j - 1] //上边界
dp[i][0] = dp[i - 1][0] // 左边界
同时，我们考虑在起点(0, 0)的情况，显然，从起点到起点只有一条路径
即dp[0][0] = 1
结合刚刚推出的这三个式子，可以发现：
dp[0][j] = dp[0][j - 1] = dp[0][0] = 1
dp[i][0] = dp[i - 1][0] = dp[0][0] = 1
到这里，递推关系已经差不多完成了，但是还有一个重要的因素马还没考虑
根据马走日的规则，马的周围有八个点都是不安全的，如图

相对于马的位置，我们把这八个点分别用8个坐标表示，即：
(1, 2) (2, 1) (-1, 2) (-2, 1) (-1, -2) (-2, -1) (1, -2) (2, -1)
将其用二维数组存储即可

最终代码

#include <iostream>
using namespace std;

long long dp[50][50];//总条数可能很多，用long long
//用二维数组存储马的控制点 
int d[8][2] = {{1, 2}, {2, 1}, {-1, 2}, {-2, 1}, {-1, -2}, {-2, -1}, {1, -2}, {2, -1}};

int main(){
	int n, m, horsex, horsey;
	cin >> n >> m >> horsex >> horsey;
	
	bool safe; //用来储存当前点的状态：安全/不安全 
	
	dp[0][0] = 1;//初始化 
	
	//二重循环遍历棋盘 
	for (int i = 0; i <= n; i++) {
		for (int j = 0; j <= m; j++) {
			safe = true;
			if (i == 0 && j == 0) continue;//跳过起点 
			if (i == horsex && j == horsey) continue;//跳过马所在的点 
			for (int p = 0; p < 8; p++) {
			//如果会被马控制，就不安全（只要在马的其中八个控制点中的其中一个） 
				if (i + d[p][0] == horsex && j + d[p][1] == horsey) {
					safe = false;
					break;
				}
			}
			if (safe) {
				//上边界 
				if (i <= 0) {
					dp[i][j] = dp[i][j - 1];
				}
				//左边界 
				else if (j <= 0) {
					dp[i][j] = dp[i - 1][j];
				}
				else {
					dp[i][j] = dp[i][j - 1] + dp[i - 1][j];
				}
			}
		}
	}
	
	//输出结果：到达(n, m)点的路径总条数 
	cout << dp[n][m] << endl;
	return 0;
}

以上是这道题的全部内容，如有错误，欢迎指出