Leetcode——初级算法（树）

最新推荐文章于 2024-08-18 14:45:23 发布

Clear_tj

最新推荐文章于 2024-08-18 14:45:23 发布

阅读量209

点赞数 1

分类专栏：算法系列文章标签： leetcode c++ 算法

本文链接：https://blog.youkuaiyun.com/Clear_tj/article/details/125032340

版权

算法系列专栏收录该内容

4 篇文章

订阅专栏

树

二叉树的最大深度

给定一个二叉树，找出其最大深度。

二叉树的深度为根节点到最远叶子节点的最长路径上的节点数。

int maxDepth(TreeNode* root) {
    if(root == NULL)    return 0;
    int depth = 0;					//层数
    queue<TreeNode*> q;				//队列
    q.push(root);					//根结点入队
    while (1)
    {
        int size = q.size();		//当前队列中个结点个数
        if (size == 0)	break;		//空队退出
        depth++;					//每一层计算之前++
        while (size--)				//只计算了当前层数的结点个数
        {
            TreeNode* temp = q.front();			//先进先出队
            if (temp->left != NULL)		q.push(temp->left);
            if (temp->right != NULL)	q.push(temp->right);	
            //左右孩子不空入队，以便累计n+1层的结点个数size
            q.pop();				//当前层数的结点依次遍历
        }
    }
    return depth;
}

题解思路：和层数有关，即层序遍历，但此题只需求出层数，故不需要读取值。使用队列，每层节点依次入队，在出队的同时将其子节点入队，直至队列为空。

验证二叉搜索树（BST）

给你一个二叉树的根节点 root ，判断其是否是一个有效的二叉搜索树。

有效二叉搜索树定义如下：

节点的左子树只包含小于当前节点的数。
节点的右子树只包含大于当前节点的数。
所有左子树和右子树自身必须也是二叉搜索树

bool isValidBST(TreeNode* root) {
    return isValidBST_Recursion(root, LLONG_MIN, LLONG_MAX);
}
bool isValidBST_Recursion(TreeNode* root, long long left, long long right)
{
    if (root == NULL)	return true;
    if (root->val <= left || root->val >= right)		//小于左值或者大于右值均false
        return false;
    //左子树最大值不能超过root->val，但最小值可以无限小，右子树反之。
    return isValidBST_Recursion(root->left, left, root->val) && isValidBST_Recursion(root->right, root->val, right);
}

题解思路：深度优先搜素，最根节点的左子树和右子树分别向下遍历，若根节点值小于左孩子值或大于右孩子值则为false，直至叶子节点

对称二叉树

给你一个二叉树的根节点 root ，检查它是否轴对称。

如下图：

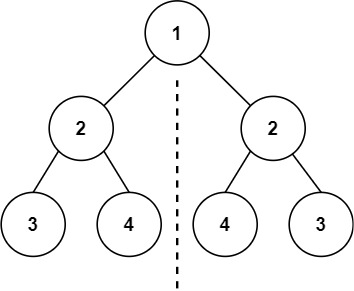
bool isSymmetric(TreeNode* root) {
    if (root == NULL)	return true;
    return helper(root->left, root->right);
}
bool helper(TreeNode* left, TreeNode* right) {
    // 都为空，返回true
    if (left == NULL && right == NULL)
        return true;
    // 一个为空则false
    else if (left == NULL || right == NULL || left->val != right->val)
        return false;
    // 再将左子树的右子树和右子树的左子树比较
    return helper(left->left, right->right) && helper(left->right, right->left);
}

题解思路：深度优先搜索，对根节点的左子树和右子树同时进行遍历，直至根节点，若值不相等或有一个为NULL，则返回false。注意递归的分别为左子树的左孩子和右子树的右孩子 以及 左子树的右孩子和右子树的左孩子，以便保持对称

二叉树的层序遍历

给你二叉树的根节点 root ，返回其节点值的 层序遍历 。（即逐层地，从左到右访问所有节点）。

vector<vector<int>> levelOrder(TreeNode* root) {
    vector<vector<int>> ar;
    if (root == NULL)	return ar;

    queue<TreeNode*> q;
    q.push(root);
    while (1)
    {
        int size = q.size();		//每层结点个数
        if (size == 0) break;		//该层无结点				
        ar.push_back(vector<int> ());
        while (size--)
        {
            TreeNode* temp = q.front();
            if (temp->left != NULL)		q.push(temp->left);
            if (temp->right != NULL)	q.push(temp->right);		//左右孩子不为空则入队
            ar.back().push_back(temp->val);							//此为二维数组的使用方法
            q.pop();												//当前结点出队
        }
    }
    return ar;
}

题解思路：和题一类似，区别在于存储每一层的值，即在题一的基础上加上每层值的存储即可。

将有序数组转换为二叉搜索树

给你一个整数数组 nums ，其中元素已经按升序排列，请你将其转换为一棵高度平衡二叉搜索树。

高度平衡二叉树是一棵满足「每个节点的左右两个子树的高度差的绝对值不超过 1 」的二叉树。

TreeNode* sortedArrayToBST(vector<int>& nums) {
    return helper(nums, 0, nums.size() - 1);
}
TreeNode* helper(vector<int>& nums, int left, int right) {
    if (left > right) {
        return nullptr;
    }

    // 若为偶数则选择数值较小的元素
    int mid = (left + right) / 2;	

    TreeNode* root = new TreeNode(nums[mid]);
    root->left = helper(nums, left, mid - 1);
    root->right = helper(nums, mid + 1, right);
    return root;
}