进制转换

前言：我们生活中习惯上用十进制数来表达数据，然而在计算机中是以二进制数来存储和表达数据的。八进制、十六进制用来缩减二进制数长度，也是经常使用的进制数，下面就来讨论下十进制与二进制、八进制、十六进制数之间的准换问题。
一、进制数的表达
十进制数，基数为十，用0~9之间的数表达。例如：6898
二进制数，基数为二，用0、1表达。例如：表达一个byte类型的8 计算机中二进制表达：0000 1000
八进制数，基数为八，用0~7之间数表达。 例如：66
十六进制数，基数为十六，用0~9，和A、B、C、D、E、F表示。例如1AB
二、在编程语言中各进制数表示
在java语言中，定义一个二进制变量前面加0b：
例如： byte a=0b1011 这个数对应于十进制的 11
定义一个八进制数，前面要加0：
例如： byte b=011 这个数对应十进制的 9
定义一个十六进制的数前面要加0X或者0x：
例如： byte c=0xC 这个数对应于十进制的 12

三、数制间的装换
其它进制转换为十进制数
如果其他进制是整数转换为十进制数，则从右向左各位数字乘以基数的幂次方。例如：
八进制数 210=08^0+1*81+28^2 结果为：8+128=136
若为小数将相应进制的数按权展成多项式，按十进制求和：
例如：
(F8C.B)16
= F×162+8×161+C×160+B×16-1
= 3840+128+12+0.6875
=3980.6875
（10011.01）2
=1×24+0×23+0×22+1×21+1×20+0×2-1+1×2-2
=16+2+1+0.25
=19.25
十进制向其他进制转换
1、 整数部分的转换
除基取余法：用目标数制的基数去除十进制数，第一次相除所得余数为目的数的最低位， 将所得商再除以基数，反复执行上述过程，直到商为“0”，所得余数为目的数的最高位。

例：（81）10=（？）2

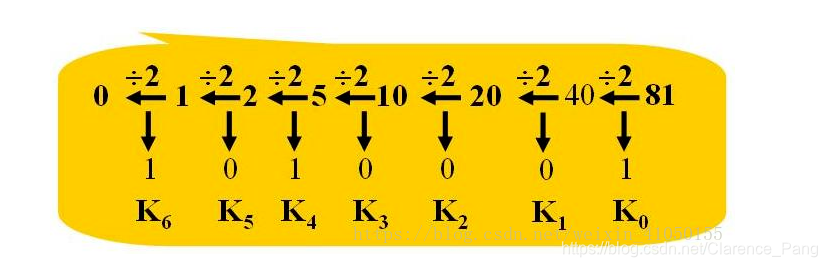
2、小数部分的转换
乘基取整法：小数乘以目标数制的基数，第一次相乘结果的整数部分为目的数的最高位，将其小数部 分再乘基数依次记下整数部分，反复进行下去，直到小数部分为“0”，或满足要求的精度为止。(如2-5， 只要求到小数点后第五位)

例： （0.65）10 =( ? )2 要求精度为小数五位。

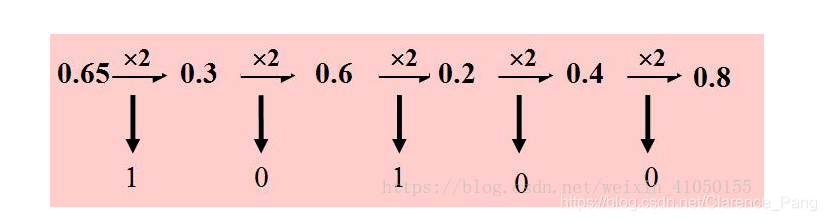
综合得：(81.65)10=(1010001.10100)2

二进制与八进制间的转换

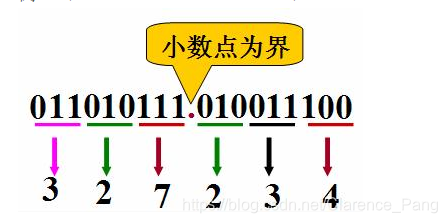
从小数点开始，将二进制数的整数和小数部分每三位分为一组，不足三位的分别在整数的最高位前和小数的最低位后加“0”补足，然后每组用等值的八进制码替代，即得目的数。

例：（11010111.0100111）2 = （327.234）8

二进制与十六进制间的转换
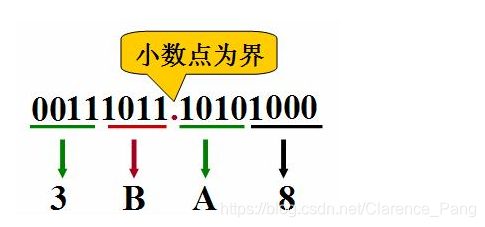
从小数点开始，将二进制数的整数和小数部分每四位分为一组，不足四位的分别在整数的最高位前和小数的最低位后加“0”补足，然后每组用等值的十六进制码替代，即得目的数。

例: (111011.10101)2=(3B.A8)16

转自：https://blog.youkuaiyun.com/weixin_41050155/article/details/79710047