密码技术应该怎么用第五天！

 随机数的重要性，随机数作用，为什么要使用密码学的随机数；简单讲一下非对称算法RSA和SM2的加密，签名，数字信封；对称算法，不多讲，推荐使用SM4_CBC,SM4_GCM模式

   说明一下：密码机必须支持的是对称密钥的ECB和CBC模式，《GMT 0018-2023 密码设备应用接口规范》规范支持了GCM和CCM模式，为了兼容之前存储数据建议使用CBC模式。接口定义建议使用GCM模式，好处多多。

随机数要具备的三个特性。

1）随机性：不存在统计学偏差，是完全杂乱的数列

2）不可预测性：不能从过去的数列推测出下一个出现的数

3）不可重现性：除非将数列本身保存下来，否则不能重现相同的数列

   随机数在密码学中广泛应用，在密钥产生过程，数字签名方案，密钥交换协议和实体鉴别协议都用到了随机数，对随机数质量的检测是保证密码产品安全的基础。现代密码算法设计理论的发展使得密码算法的强度得到了严谨的论证，很难直接破解。然而，所有密码算法的安全都依赖于高质量的随机数，如果随机数发生器被植入后门，则所有的安全性论证都失去了基础。当前，如何使用密码算法在随机数发生器被植入后门的情况下仍能安全工作，已经成为一个新的设计目标。

1）生成密钥，用于对称密码和消息验证码

2）生成密钥对，用于公钥密码和数字签名

3）生成初始化向量IV，用于分组密码的CBC、CFB和OFB模式

4）生成nonce，用于防御重放攻击以及分组密码的CTR模式等

5）生成盐，用于基于口令的密码PBE等

   注意：在保护口令中，有人喜欢使用随机数作为盐和口令一起走SM3，不推荐这样使用，盐的保护一般比较弱，推荐使用HMAC-SM3使用密钥来保护数据。

   特别强调一下,如果随机数被预测，那么安全的基础就不存在，所以使用密码学随机数是必须的选择！

java.util.Random 应该替换为 java.security.SecureRandom。

Random 只具备随机性,不具备不可预测性,不能用于密码算法.

Python 的 random.random() 应该替换为 os.urandom(n)  / secrets.token_bytes(n)

• 公钥算法：RSA，SM2

说明：SM2加密和签名都用到了随机数，所以每次加密和签名的结果都不一样！

SM2相当于3072位的RSA算法。加密对比如下

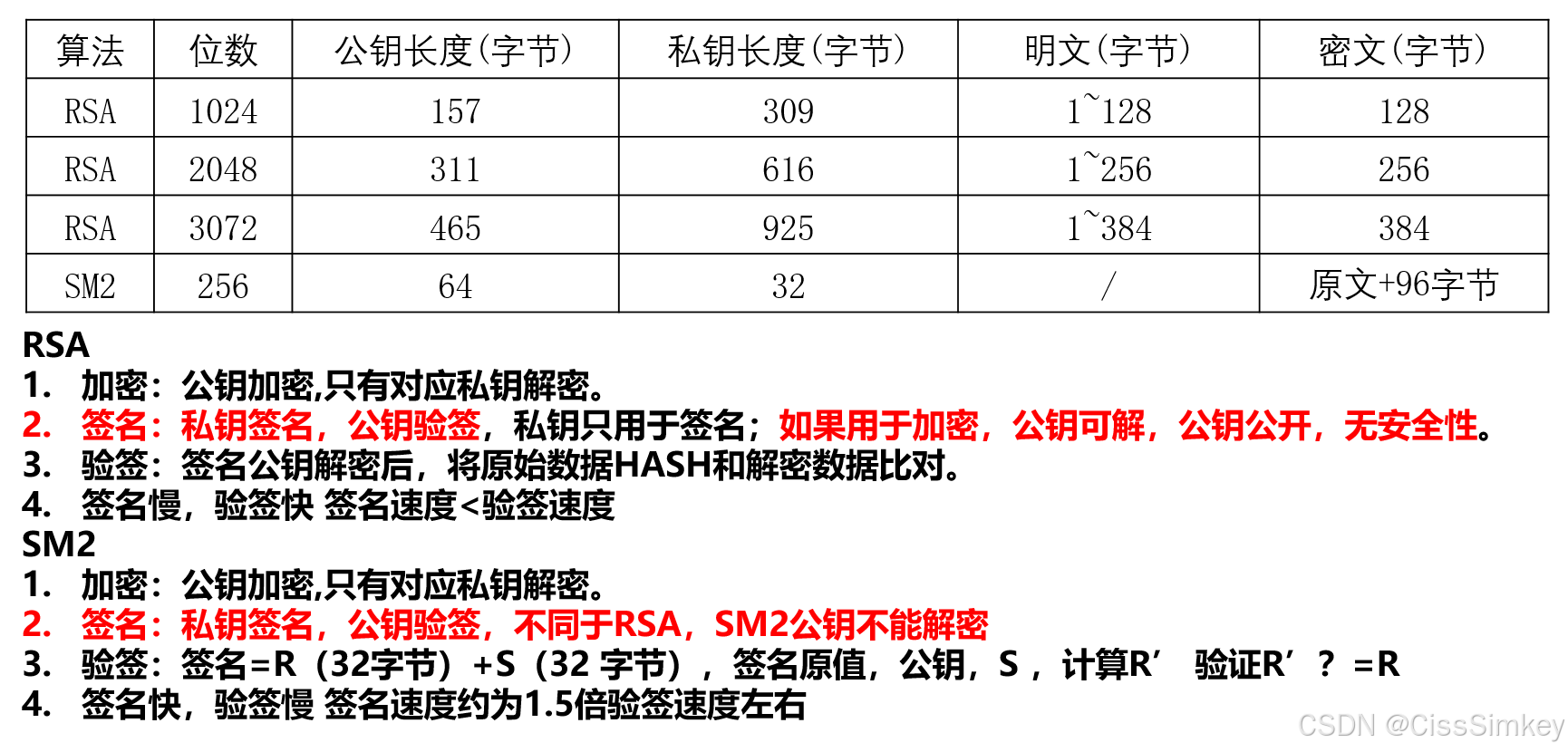
SM2的加密格式，为什么会增加96字节

1、密钥更短，私钥长32字节，公钥长64字节

2、签名速度快，验签速度慢，签名原始数据长度无限制，签名结果为64字节

3、加密运算支持可达128G字节数据长度，加密结果增加96字节。

密文格式：C1C3C2 

C1C3C2的长度=C1【X 32字节+Y32字节】+C3【32字节】+C2

               =明文长度+96字节

   C1：x分量【32字节】，以及y分量【32字节】的最低位

   C3：明文的杂凑值【32字节】

C3 用于验证消息的完整性和真实性，通过对明文消息和其他相关参数（如加密过程中的一些临时变量等）进行 SM3 哈希计算得到

   C2：密文

• RSA签名验签说明：

签名过程：

    摘要信息用发送者的私钥加密，与原文一起传送给接收者

    1. 摘要=Hash（原文），Hash=md5/SHA1/SHA256

    2. 签名=私钥（摘要）

    3. Send（原文【摘要】，公钥，签名）

验签过程：

     接收者只有用发送者的公钥才能解密被加密的摘要信息，

     然后用HASH函数对收到的原文产生一个摘要信息，与解密的摘要信息对比

    1.摘要’= 公钥（签名）

    2.摘要   = Hash（原文）

    3.比对 摘要’和 摘要

RSA公钥加密，私钥解密。私钥加密，公钥可以解密，务必注意不要使用私钥加密。

• SM2签名验签说明：

签名过程：

设待签名的消息为M，为了获取消息M的数字签名(r,s)，作为签名者的用户A应实现以下运算步：

1、摘要=Hash(原文）HASH=SM3； 

2、计算R=(摘要，椭圆曲线点[k]G) mod n；

3、计算S= (随机数k，私钥) mod n，；

4、签名值=R+S；

5、Send(原文[摘要]，签名值，公钥)

验签过程：

为了检验收到的消息M′及其数字签名(r′, s′)，作为验证者的用户B应实现以下运算步骤：

1、摘要′=Hash(原文)；Hash=sm3

2、计算R=(公钥，s ′,摘要′ ,椭圆曲线点[k]G) mod n；

3、检验R= r′是否成立，若成立则验证通过，否则验证不通过 。

签名快，验签慢 签名速度约为1.5倍验签速度

• 数字信封

   数字信封是指发送方，使用接收方的公钥来加密对称密钥，对称密钥加密数据，其目的是用来确保对称密钥传输的安全性。采用数字信封时，接收方需要使用自己的私钥才能打开数字信封得到对称密钥。

   加密 1. 对称密钥(数据），2.公钥（对称密钥）

   解密 1.私钥(对称密钥），2.对称密钥（数据）

数字信封【混合密码】sm2样例：

public_key:67568101EA1452B30BA7F0D0C5791DC0E4A82BE0D6BF943C959AA2639C31E1C0D675642BFE607298946776C44E22D019BB01820C6C920C9740750E9E4D19968B

private_key:DE81230C7E1411EF26B94EEE51F68746407CC9DB032952C7B1B8B07E57F535EA

sm4_key:3C2DF56EE7C4FF30552FD09C082ADF46

plain_text='1'

加密

1.对称密钥加密（数据）cipher_text=sm4_ecb_encrypt(plain_text)

=57DF4E0CB79DD6C1D5F4B20A90FEC2C3

2.公钥（对称密钥）cipher_key=sm2_encrypt(sm4_key)

=5E3DC7BA2CFF291CC9069CAD24DED80D002E688B3EC80374AB112372A25A088D37F158BB7B3121263A3740C63521A4474CDA567712BAAC7804EA446994E79A3134E372C563CA72A725C0D3062EA43C97CD4E41A0D3B93E71225EC1C1809B0AD1FE7AF8AB4A4D49237AD69F470A16CD8392D274D9A0A3D51A3F4A09B29281AC79

解密

1.私钥（对称密钥）sm4_key =sm2_decrypt(cipher_key)

=3C2DF56EE7C4FF30552FD09C082ADF46

2.对称密钥解密plain_text=sm4_ecb_decrypt(cipher_text）=

sm4_ecb_decrypt(57DF4E0CB79DD6C1D5F4B20A90FEC2C3)=1

那么问题来了，数字信封的公钥强度和对称算法强度应该相当，如果一个强，一个弱，那么我们只需要攻击弱的就可以了。如果对称密码非常弱，那么公钥算法再强也没用。

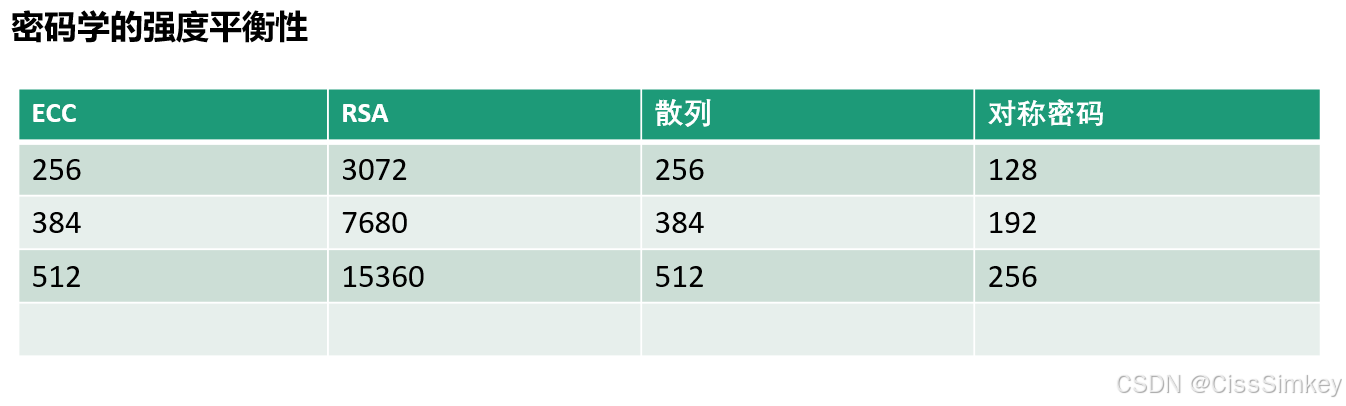
公钥密码的密钥长度不能直接与对称密码的密钥长度进行比较

具备同等抵御暴力破解强度的密钥长度比较

个人理解：SM1，SM4(128)>=SM2（RSA3072）>RSA2048