泛型递归_树的递归_力扣精选_07

最新推荐文章于 2022-11-11 11:48:27 发布

原创最新推荐文章于 2022-11-11 11:48:27 发布 · 236 阅读

0 ·

CC 4.0 BY-SA版权

文章标签：

#leetcode #二叉树 #数据结构 #面试 #算法

leetcode 专栏收录该内容

6 篇文章

订阅专栏

本文深入解析了LeetCode上的经典算法题目，包括爬楼梯、括号生成、翻转二叉树、验证二叉搜索树等，提供了详细的解题思路和代码实现，探讨了递归、动态规划等算法技巧。

1. 题目

2 题目解析

思维要点

不要人肉进行递归（最大误区）
找到最近最简方法，将其拆解成可重复解决的问题(重复子问题）
数学归纳法思维
T70. 爬楼梯
思路递归
模板

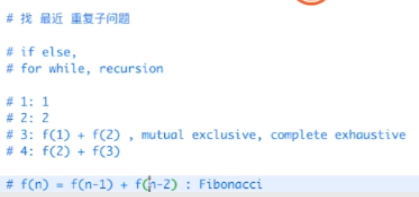
step 1 递归终止条件此处为 extra_step != 0
step 2 处理当前层此处为 all_ways = one_step_before + two_step_before
step 3 下探到下一层此处为two_step_before = one_step_before \ one_step_before = all_ways \ extra_step -= 1
step 4 清理当前层（此处非必要）

class Solution:
    def climbStairs(self, n: int) -> int:
        if n == 1:
            return 1
        if n == 2:
            return 2 
        
        one_step_before = 2 
        two_step_before = 1
        extra_step = 0
        if n > 2:
            extra_step = n - 2
            while extra_step != 0:
                all_ways = one_step_before + two_step_before
 
                two_step_before = one_step_before
                one_step_before = all_ways
                extra_step -= 1
        return all_ways

时间复杂度O(1)

T22. 括号生成
先写模板再写
第四部没有动用全局变量

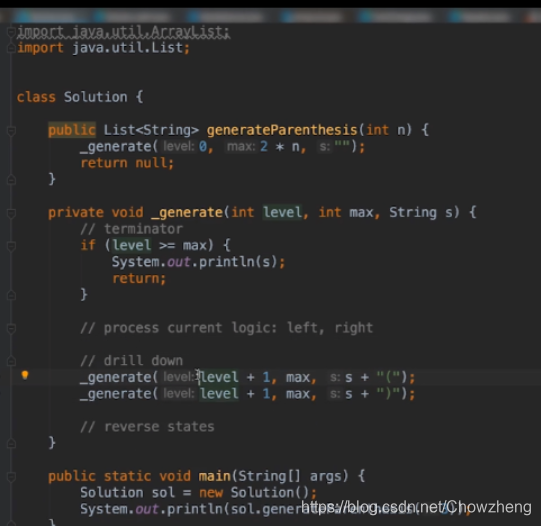
只用这两个逻辑即可

时间复杂度O(nlogn)

T226. 翻转二叉树

class Solution:
    def invertTree(self, root: TreeNode) -> TreeNode:
        if root is None:
            return []
        root.left , root.right = root.right , root.left
        self.invertTree(root.left)
        self.invertTree(root.right)
        return root

时间复杂度O(nlogn)?
优化解法
4. T98. 验证二叉搜索树
在这里插入图片描述

时间复杂度O(nlogn)?
优化解法
中序遍历

104. 二叉树的最大深度

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = None

class Solution:
    def maxDepth(self, root: TreeNode) -> int:
        if root is None:
            return 0
        else:
            left_height = self.maxDepth(root.left)
            right_height = self.maxDepth(root.right)
            return max(left_height,right_height) +1

时间复杂度O(n)
6. 111. 二叉树的最小深度
step_1 if not root —> 0
step_2 if root.left and root.right exist —> 1
step_3 遍历左右节点

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = None

class Solution:
    def minDepth(self, root: TreeNode) -> int:
        if root is None:
            return 0
        children = [root.left,root.right]
        if not any(children):
            return 1
        min_depth = float("inf")
        for c in children:
            if c:
                min_depth = min(self.minDepth(c),min_depth)

        return min_depth + 1