数据结构_树_二叉树_二叉搜索树

1基础概念,树的定义

Linked List 是特殊化的 Tree
Tree 是特殊化的Graph

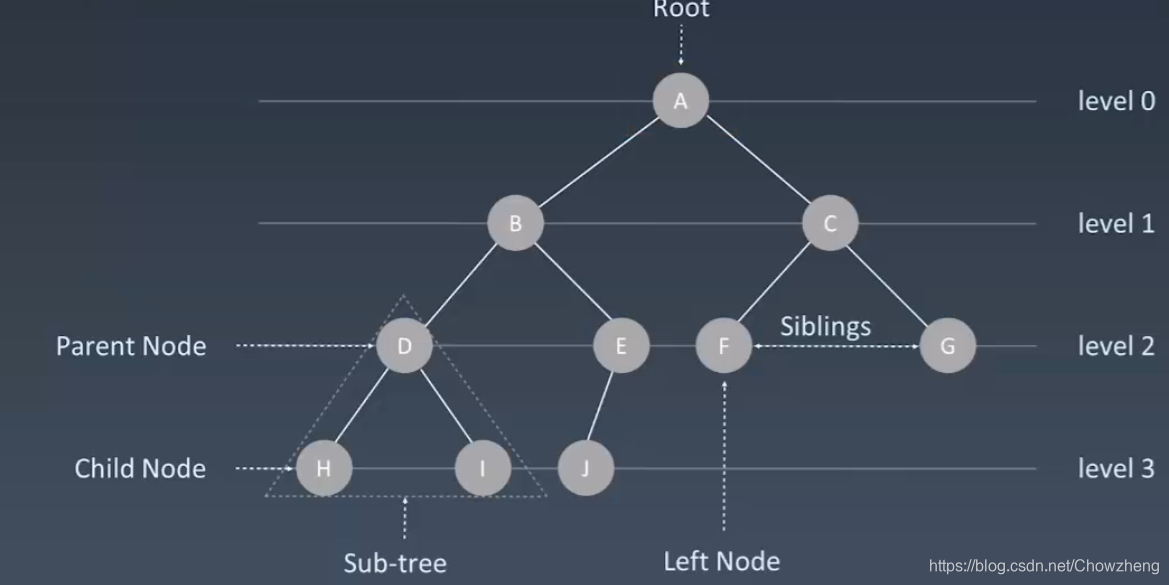
2二叉树

使用以下函数创建并操作二叉树。

BinaryTree()
getLeftChild()
getRightChild()
setRootVal(val)
getRootVal()
insertLeft(val)
insertRight(val)

2.1 列表之列表

使用‘列表之列表’表示树

2.1.1 列表函数BinaryTree

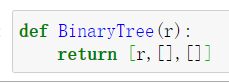
2.1.2 插入左子树

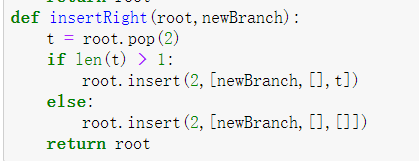
2.1.3 插入右子树

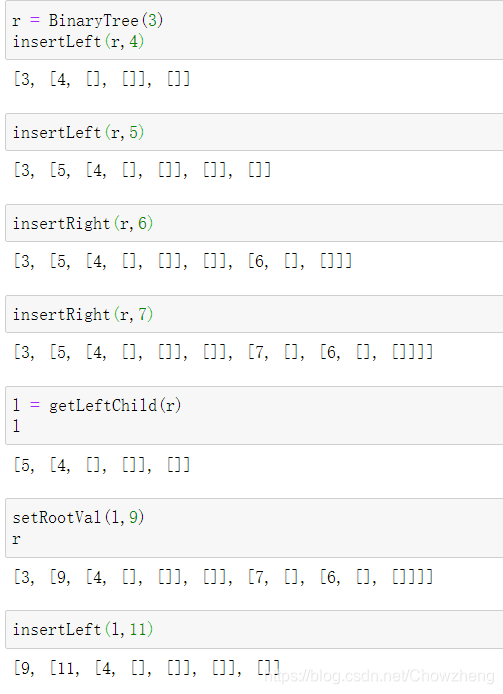
2.1.4 树的访问函数

2.2 节点与引用

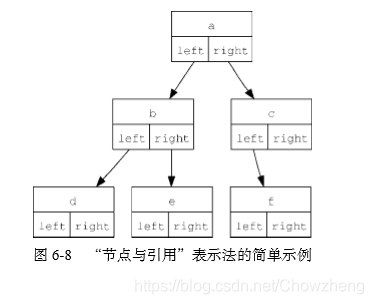
首先我们定义一个简单的类，如下所示。
‘节点与引用’表示法的要点是，属性left和right会指向 BinaryTree
类的其他实例。举例来说，在数中插入新的左子树时，我们会创建另一个BinaryTree实例，并将根节点的 self.leftChild改为指向新树

class BinaryTree:
    def __init__(self,rootObj):
        self.key = rootObj
        self.leftChild = None
        self.rightChild = None
    def insertLeft(self,newNode):
        if self.leftChild == None:
            self.leftChild = BinaryTree(newNode)
        else:
            t = BinaryTree(newNode)
            t.leftChild = self.leftChild
            self.leftChild = t
    def insertRight(self,newNode):
        if self.rightChild == None:
            self.rightChild = BinaryTree(newNode)
        else:
            t = BinaryTree(newNode)
            t.rightChild =self.rightChild
            self.rightChild = t
    def getRightChild(self):
        return self.rightChild
    def getLeftChild(self):
        return self.leftChild
    def setRootVal(self,obj):
        self.key = obj
    def getRootVal(self):
        return self.key

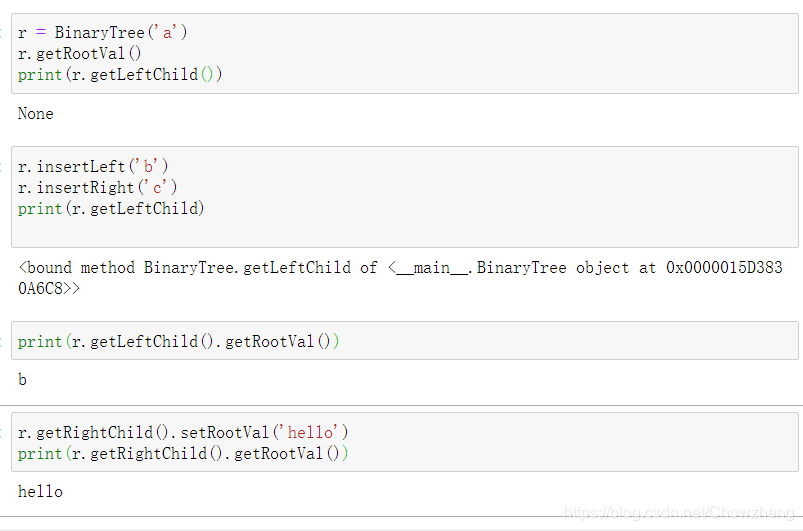
2.2.1 解析树

2.2.2 树的遍历

前序遍历 (pre-order) 根左右
中序遍历 (in-order) 左根有
后序遍历 (post-order) 左右根

2.3 二叉搜索树

在实现搜索树之前，我们来复习一下映射抽象数据类型提供的接口。你会发现，这个接口类 似于 Python字典.

• Map() 新建一个空的映射。
• put(key,val) 往映射中加入一个新的键–值对。如果键已经存在，就用新值替换旧值.
• get(key) )返回 key 对应的值。如果 key 不存在，则返回 None。
• del 通过 del map[key]这样的语句从映射中删除键–值对。
• len() 返回映射中存储的键–值对的数目。
• in 通过 key in map 这样的语句，在键存在时返回True

2.3.1 搜索树的实现

二叉树依赖这样的一个性质，小于父节点的都在左子树中，大于父节点的都在右子树中。我们将这个性质成为二叉搜索性。

class BinarySearchTree:
    def __init__(self):
        self.root = None
        self.size = 0
    def length(self): 
        return self.size
    def __len__(self):
        return self.size
    def __iter__(self):
        return self.root.__iter__()
class TreeNode:
    def __init__(self,key,val,left = None,right = None,parent = None):
        self.key = key
        self.payload = val
        self.leftChild = left
        self.rightChild = right
        self.parent = parent
    def hasLeftChild(self):
        return self.leftChild
    def hasRightChild(self):
        return self.rightChild
    def isLeftChild(self):
        return self.parent and \ 
    self.patent.leftChild == self
    def isRightChild(self):
        return self.parent and \ 
    self.parent.rightChild == self
    def isRoot(self):
        return not root.parent
    def isLeaf(self):
        return not (self.rightChild or self.leftChild)
    def hasAnyChildren(self):
        return self.leftChild or self.rightChild
    def hasBothChildren(self):
        return self.rightChild and self.leftChild
    def replaceNodeData(self,key,value,lc,rc):
        self.key = key
        self.payload = value
        self.leftChild = lc
        self.rightChild = rc
        if self.hasLeftChild():
            self.leftChild.parent = self
        if self.hasRightChild():
            self.rightChild.parent = self
    
        
        

引用

python 数据结构与算法分析 布拉德利-米勒 等 吕能等译