Leetcode【快慢指针】| 287. 寻找重复数

题目

给定一个包含 n + 1 个整数的数组 nums，其数字都在 1 到 n 之间（包括 1 和 n），可知至少存在一个重复的整数。假设只有一个重复的整数，找出这个重复的数。
示例 1:
　输入: [1,3,4,2,2]
　输出: 2
示例 2:
　输入: [3,1,3,4,2]
　输出: 3
说明：
　不能更改原数组（假设数组是只读的）。
　只能使用额外的 O(1) 的空间。
　时间复杂度小于 O(n²) 。
　数组中只有一个重复的数字，但它可能不止重复出现一次。
来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/find-the-duplicate-number

解题

 按照暴力思路这道题很容易解，比如数组排序后依次遍历找重复，比如用哈希表存储遍历找已遍历到的，比如暴力依次将每个数与数组中其他数依次比较看是否重复，但是由于题目中要求不能更改原数组(所以不能排序)，只能使用额外的O(1)空间(所以不能用额外的数据结构存储)，时间复杂度小于O(n²)所以不能暴力比较，重复数字还不止一个所以不能用数组求和和再减去1到n数的和来求出唯一重复的数，故需要用到以下几种常用的算法思路来解决。

快慢指针找环的入口

 这个思路很巧妙，因为注意到数组有n+1个数，所以索引是0到n，而数组中的数值也是限制在1到n中间的。所以索引和对应的数值的取值范围相同，可以用数值当作索引。
　故我们可以设置一个i－＞nums[i]的对应，对nums[]建图，对于每个 i 结点加一条i－＞nums[i]的边。
　因为存在一个重复的数，所以除0外在nums[]中的结点个数<=n个，而边有n条边，对于重复的数target来说，必然存在>=2条边指向这个数，所以i->nums[i]->nums[nums[i]]->…的过程中必然会出现一个环。问题就变为了链表找环问题，而环的入口就是重复的数target。
　设置一个快慢指针，能判断除是否出现环，如果有环，快慢指针会相遇环中的任意一个结点。如何寻找环的入口成为下一个问题。
　快慢指针同时从起点出发，假设从快慢指针到环的入口距离为a，环的入口到相遇问题距离为b。那么慢指针到达相遇位置走了a+b步。
　
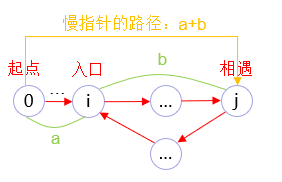
　此时快指针走的是2(a+b)步。
　用另一种想法，快指针到环的入口距离为a步，因为相遇时快指针肯定是比慢指针多走了完整的k圈，假设一个环是L步，那么此时快指针走的步数是a+b+kL步。所以有2(a+b) = a+b+kL =>a = kL-b = (k-1)L+L-b。（L-b是从相遇点再到入口的距离）
　
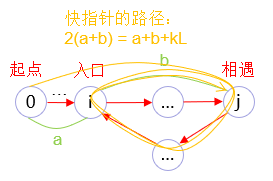
　所以将一个指针从起点开始走，走a步就到环的入口，即target。
　另一个指针从相遇点开始走，同样走a步也就是(k-1)L+k-b步，相当于从起点开始走a+b+(k-1)L+k-b = a+kL步，到达的点同样是入口。所以将慢指针从0开始出发，快指针从相遇点开始出发，每次都只走一步，再次相遇的点就是环的入口。
　时间复杂度：O(n)
　空间复杂度：O(1)
　类似的思路也可以用于Leetcode 160.相交链表。

class Solution {
    public int findDuplicate(int[] nums) {
        //快慢指针  太绝了  总共有n+1个数索引是0到n,而数字都在1到n中间，所以可以建立一个i->nums[i]的链表，使用快慢指针 看是否有环
        //用快慢指针找出相遇点
        int slow = nums[0];
        int fast = nums[nums[0]];
        while(fast != slow){
            fast = nums[nums[fast]];
            slow = nums[slow];
        }
        //快指针从相遇位置出发，慢指针从起点出现，再次相遇就是环的入口
        slow = 0;
        while(fast!=slow){
            fast = nums[fast];
            slow = nums[slow];
        }
        return slow;
    }
}

二分查找

 nums[]数组中的数值范围为1到n，一共有n+1个数。因为存在重复的数target，除target以外的数都只出现一次。所以：

1. 对于<target的数i来说，数组中存在<=i的数的个数count[i]是<=i的。
2. 对于>=target的数i来说，数组中存在<=i的数的个数count[i]是>i的。

所以可以根据数组中存在<=i的数的个数对1到n的数进行二分查找。找到转折点count[i]>i的第一个数即为target。
　因为二分查找的时间复杂度是O(logn)，每次二分查找时都需要遍历一遍数组O(n)计算count[i]来判断count[i]与i的大小关系，所以一共时间复杂度为O(nlogn)，每次计算count[i]不用存储起来，直接用一个变量count临时计算即可，故空间复杂度为O(1)。

class Solution {
    public int findDuplicate(int[] nums) {
        //二分查找，i= 1到n数二分查询，数组中小于等于i的数count有几个，重复数之前count<=i,重复数之后count>i
        //时间复杂度O(logn)
        int n = nums.length-1;
        int l = 1, r = n;//因为小于等于n的数已知
        int res = -1;
        while(l<=r){
            int count = 0;
            int mid = l+(r-l)/2;
            for(int i = 0; i <= n; i++){
                if(nums[i]<=mid){
                    count++;
                }
            }
            if(count>mid){//说明重复数在mid之前
                r = mid-1;
                res = mid;
            }else{
                l = mid+1;
            }
        }
        return res;
    }
}

参考：力扣官方题解