Leetcode【DFS BFS 数组 队列】| 面试题13. 机器人的运行范围

题目

地上有一个m行n列的方格，从坐标 [0,0] 到坐标 [m-1,n-1] 。一个机器人从坐标 [0, 0] 的格子开始移动，它每次可以向左、右、上、下移动一格（不能移动到方格外），也不能进入行坐标和列坐标的数位之和大于k的格子。例如，当k为18时，机器人能够进入方格 [35, 37] ，因为3+5+3+7=18。但它不能进入方格 [35, 38]，因为3+5+3+8=19。请问该机器人能够到达多少个格子？
示例 1：
　输入：m = 2, n = 3, k = 1
　输出：3
示例 2：
　输入：m = 3, n = 1, k = 0
　输出：1
提示：1 <= n,m <= 100 ；0 <= k <= 20
来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/ji-qi-ren-de-yun-dong-fan-wei-lcof

解题

思路分析

将题目求解的"机器人能到达的格子"细分，主要有两点要求：

1. 在m x n个格子里，坐标的数位之和<=k。
   这个简单，由题中例子可知，数位之和就是i_m/10+i_m%10+j_n/10+j_n%10
2. 机器人从[0,0]坐标开始移动，每次只能向左/右/上/下移动一格，且不能移出m x n的方格外。这个条件就需要详细思考了。
   如果想着简单的遍历所有的格子求数位之和<=k那就naive了。因为你会发现同时满足这两个条件不是那么简单的。
   当m，n为两位数时，满足数位之和<=k的情况可能是不连通的。也就是说有可能有格子满足条件一(数位之和<=k)，但是也满足不了条件2(机器人到达不了)。
   如下图(方格内为数位之和，方格外标注为行列坐标)。可以看出能将所有方格分为若干个10x10的子方格。在每个子方格中当m,n在不同的十位数范围内时(如10 ~ 19，20 ~ 29等)，数位之和又从头开始增大，但是每次又不是从0开始，有从1开始的，从2开始的，从3开始的…这使得当k为不同的数时，哪些子方格能连通的情况相当复杂，我们无法一一列举出来。
   
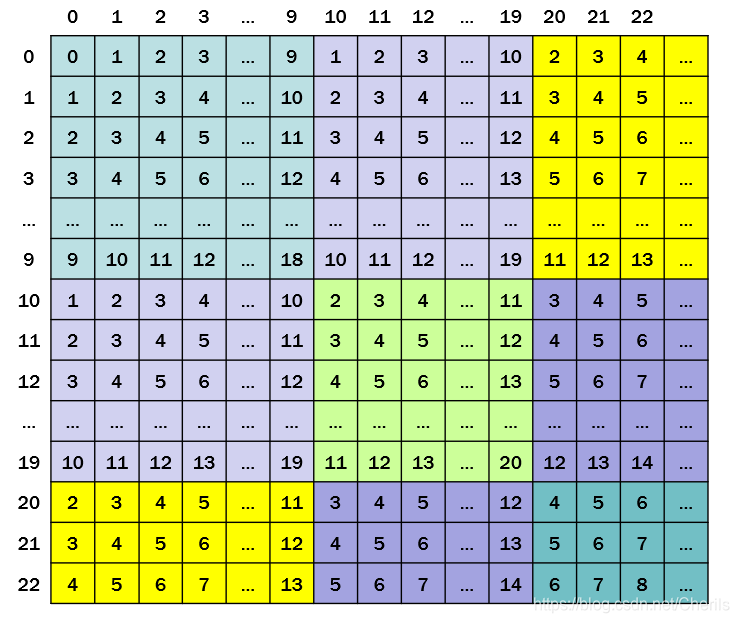
   当k为不同情况时，满足数位之和条件的格子情况如下：
   
   
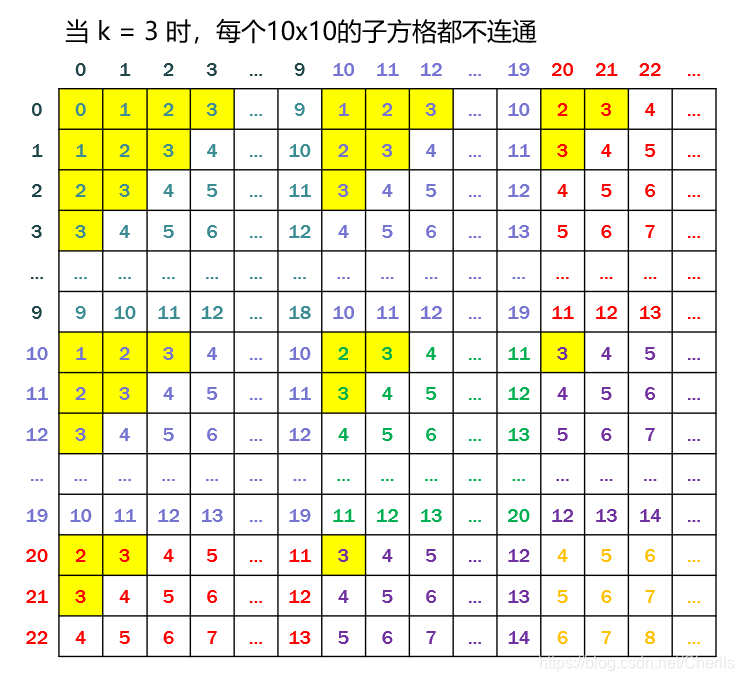
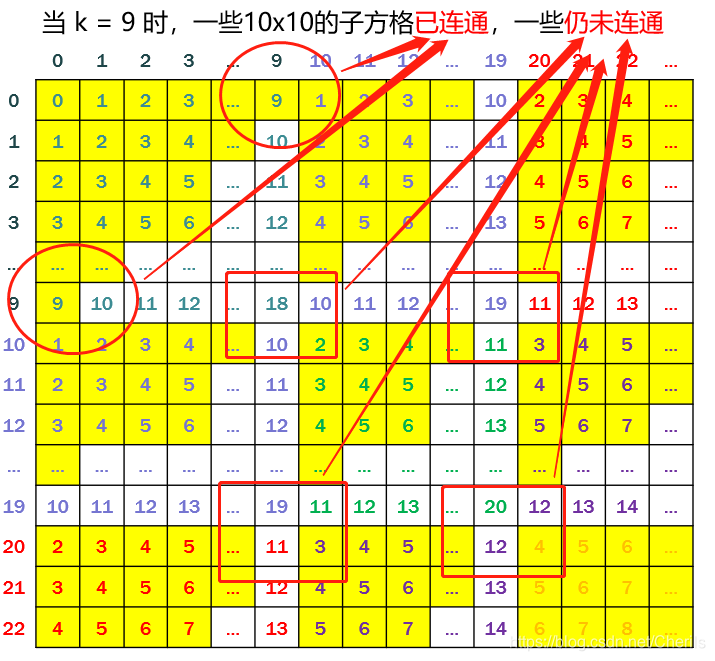
   当k越大，m、n也越大的时候，越多的10x10子方格能够连通起来。
   那么同时满足两个条件这一问题就转变为如何遍历整个方格了。简单来说，要有顺序，我们就模仿机器人的移动规则，从[0,0]开始，只需向右和向下两个方向，就可以全部遍历完整个方格，没走一步判断一次，接下来是两种按机器人的移动规则遍历的方法。

DFS和BFS解法

 首先不难想到的是深度优先遍历和广度优先遍历的办法。这两个搜索方法的讲解详见图/树的遍历：深度优先遍历DFS和广度优先遍历BFS详解与java实现。

DFS实现

 设置一个是否可达(已访问)的字段isVisited[i][j]作标记。

class Solution {
    public int movingCount(int m, int n, int k) {
        //dfs 递归
        //判断特殊情况
        if(m<=0 || n<=0 || k<0){
            return 0;
        }
        //定义并初始化标记字段和结果字段
        boolean[][] isVisited  = new boolean[m][n];
        return recursive(m,n,0,0,k,isVisited);
    }

    public int recursive(int m, int n, int i, int j, int k, boolean[][] isVisited){
        //特殊情况，方格外/数位之和不符合/不可达
        if(i<0 || i>=m || j<0 || j>=n || Sum(i,j)>k || isVisited[i][j]){
            return 0;
        }
        
        isVisited[i][j] = true;
        return recursive(m,n,i+1,j,k,isVisited)+recursive(m,n,i,j+1,k,isVisited)+1;
    }
    //计算数位之和
    public int Sum(int i, int j){
        int sum = 0;
        // sum = i%10 + i/10 + j%10 + j/10;
        while(i!=0){
            sum += i%10;
            i = i/10;
        }
        while(j!=0){
            sum += j%10;
            j = j/10;
        }
        return sum;
    }
}

BFS实现

 从(0,0)开始，依次遍历其邻接点（右/下邻接点），再遍历邻接点的邻接点。用队列实现(队列保存坐标)：将初始点加入队列开始，弹出一个点，res++说明可达的点多一个，然后判断其邻接点是否可达，若可达表明该店可以是邻接点加入队列中，然后继续弹出队头元素…。

class Solution {
    public int movingCount(int m, int n, int k) {
        //bfs 队列
        //判断特殊情况
        if(m<=0 || n<=0 || k<0){
            return 0;
        }
        //定义并初始化标记字段和结果字段
        boolean[][] isVisited  = new boolean[m][n];
        int res = 0;

        Queue<int[]> queue = new ArrayDeque<>();
        queue.add(new int[]{0,0});//队列的每个元素保存坐标(i，j)
        while(!queue.isEmpty()){
            int[] poll = queue.poll();
            res++;
            if(poll[0]+1 <m && Sum(poll[0]+1,poll[1])<=k && !isVisited[poll[0]+1][poll[1]]){//判断下邻接点（坐标在方格内，数位之和不大于k,仍未访问过，就可当作下一个邻接点）
                queue.add(new int[]{poll[0]+1,poll[1]});
                isVisited[poll[0]+1][poll[1]] = true;
            }
            if(poll[1]+1 <n && Sum(poll[0],poll[1]+1)<=k && !isVisited[poll[0]][poll[1]+1]){//判断右邻接点（坐标在方格内，数位之和不大于k,仍未访问过）
                queue.add(new int[]{poll[0],poll[1]+1});//将其加入队列中，方便下一次判断它的邻接点（右/下）
                isVisited[poll[0]][poll[1]+1] = true;//将其标记未访问过。
            }
        }
        return res;
    }

    //计算数位之和
    public int Sum(int i, int j){
        int sum = 0;
        // sum = i%10 + i/10 + j%10 + j/10;
        while(i!=0){
            sum += i%10;
            i = i/10;
        }
        while(j!=0){
            sum += j%10;
            j = j/10;
        }
        return sum;
    }
}

递推解法

 机器人从左上角出发，我们可以将搜索的方向由四个方向缩减为只用向右或向下移动。可以通过递推来判断该格子是否可达。因为只要它的左边格子或者上面格子可达，这个格子必然可达。所以递推公式为：
　isVisited[i][j] = isVisited[i-1][j] or isVisited[i][j-1] and sum[i][j] < k
　(isVisited[i][j]表示（i,j）格子是否可达，sum[i][j]表示数位之和)

class Solution {
    public int movingCount(int m, int n, int k) {
        //递推，只需向右或向下两个方向
        //判断特殊情况
        if(m<=0 || n<=0 || k<0){
            return 0;
        }
        ////标识是否可达字段并初始化,1表示可达,0表示不可达
        boolean[][] isVisited = new boolean[m][n];
        int res = 1;
        //初始化第一个位置
        isVisited[0][0] = true;
        //先计算第一列可达的
        for(int i = 1; i < m; i++){
            isVisited[i][0] = isVisited[i-1][0] && Sum(i,0)<=k;
            // if(isVisited[i][0] == true){
            //     res++;
            // }
            res = isVisited[i][0]?res+1:res;
        }
        //再计算第一行可达的
        for(int j = 1; j < n; j++){
            isVisited[0][j] = isVisited[0][j-1] && Sum(0,j)<=k;
            res = isVisited[0][j]?res+1:res;
        }
        //最后看其他位置的(都是从第一行/第一列递推过来的)
        for(int i = 1; i < m; i++){
            for(int j = 1; j < n; j++){
                isVisited[i][j] = (isVisited[i-1][j] || isVisited[i][j-1]) && Sum(i,j)<=k;
                res = isVisited[i][j]?res+1:res;
            }
        }
        return res;
    }
    //计算数位之和
    public int Sum(int i, int j){
        int sum = 0;
        // sum = i%10 + i/10 + j%10 + j/10;
        while(i!=0){
            sum += i%10;
            i = i/10;
        }
        while(j!=0){
            sum += j%10;
            j = j/10;
        }
        return sum;
    }
}

参考:
[1]力扣题解
[2] LeetCode面试题13：机器人的运行范围-wyplj_sir
[3] Leetcode 面试题13 - 机器人的运动轨迹-Flora_xuan1993