排序学习4之归并排序

归并排序

归并排序的基本操作是将两个已经排序的表合并在一起。因为两个表是已经排好序的，所以若将输出放到第三个表中，可以通过对输入数据一趟排序来完成。所以归并排序以最坏复杂度O(nlogn)的情形运行。

步骤

因为需要合并两个已经排序的表到第三个表中。所以该过程需要三个表，也就对应需要三个计数器。他们初始置于对应数组的开始端，两个计数器对应的数组的值较小的被放到第三个表中，有操作的数组计数器向前进一步，重复以上操作。若其中某个数组全部进入到第三个数组中，则将另一个数组中的元素一次放到第三个数组中。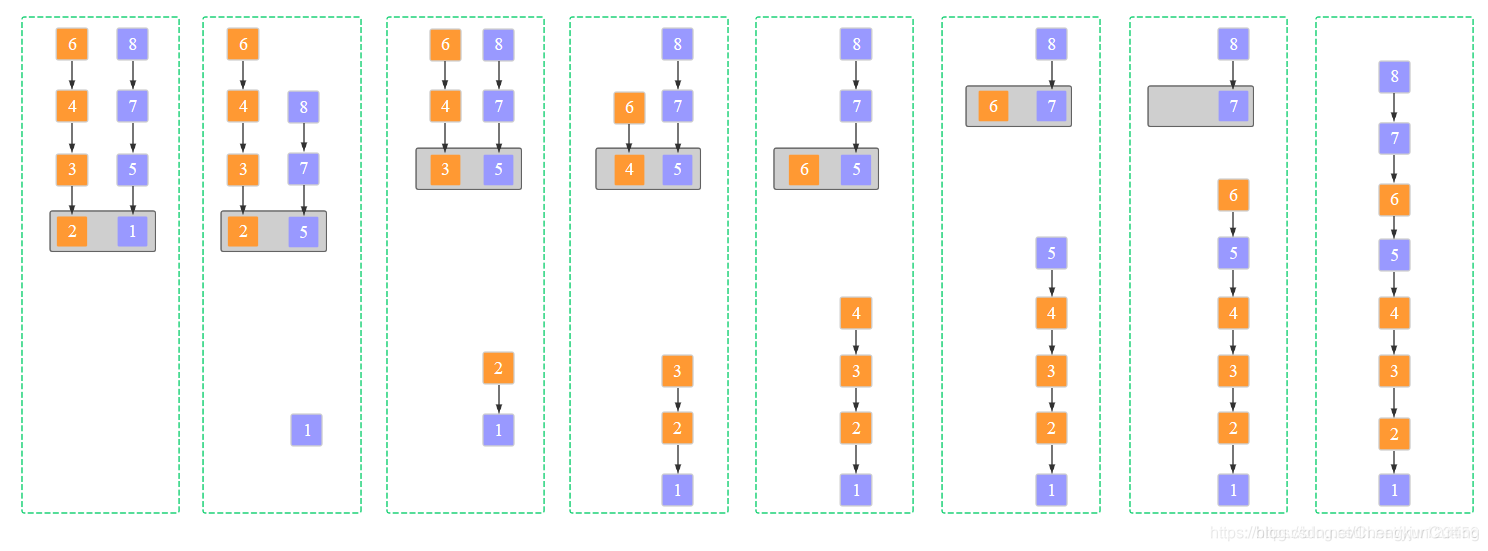

public class MergeSort {

    public static void merSort(int[] arr,int left,int right){

        if(left<right){
            int mid = (left+right)/2;
            merSort(arr,left,mid);//左边归并排序，使得左子序列有序
            merSort(arr,mid+1,right);//右边归并排序，使得右子序列有序
            merge(arr,left,mid,right);//合并两个子序列
        }
    }
    private static void merge(int[] arr, int left, int mid, int right) {
        int[] temp = new int[right - left + 1];//ps：也可以从开始就申请一个与原数组大小相同的数组，因为重复new数组会频繁申请内存
        int i = left;
        int j = mid+1;
        int k = 0;
        while(i<=mid&&j<=right){
            if (arr[i] < arr[j]) {
                temp[k++] = arr[i++];
            } else {
                temp[k++] = arr[j++];
            }
        }
        while(i<=mid){//将左边剩余元素填充进temp中
            temp[k++] = arr[i++];
        }
        while(j<=right){//将右序列剩余元素填充进temp中
            temp[k++] = arr[j++];
        }
        //将temp中的元素全部拷贝到原数组中
        for (int k2 = 0; k2 < temp.length; k2++) {
            arr[k2 + left] = temp[k2];
        }
    }
    
    

}

注
虽然归并排序的运行时间为O(nlogn)，但是他有一个明显的问题，即合并两个已经排序的表用到线性附加内存。在整个算法中还要花费将数据拷贝到临时数组再拷回来这样一些附加的工作，他明显减慢了排序的速度。