堆排序:
时间复杂度O(nlogn) 空间复杂度O(1) 稳定性:不稳定
堆排序用的是树形结构 ,把数组写成二叉树
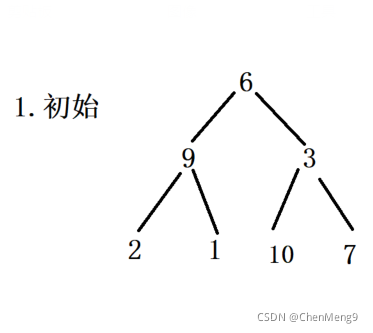
接下来的思想类似于冒泡 ,把数组调成大顶堆,就是大的数在上,小的在下,顶端就是最大的树,因为要确保把最大的数调到顶端 ,所以第一次从最小的结点开始依次往上调
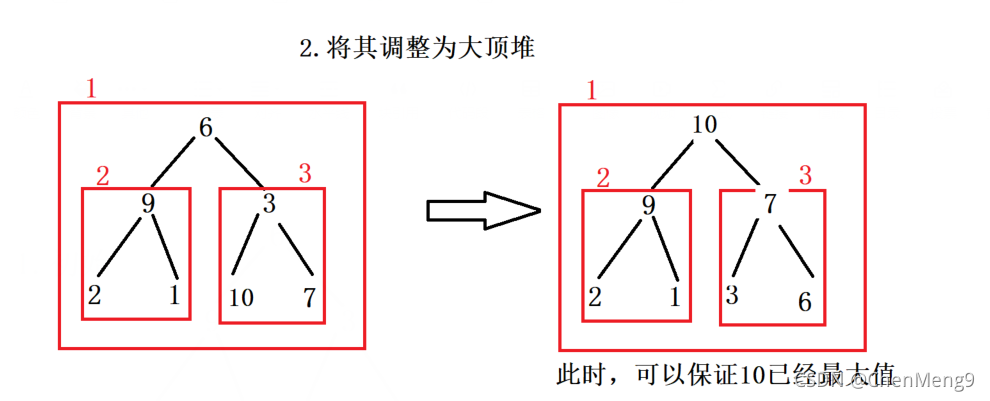
调好之后 ,将顶端的数和最后一个数交换位置 ,并剔除最后一个数 。
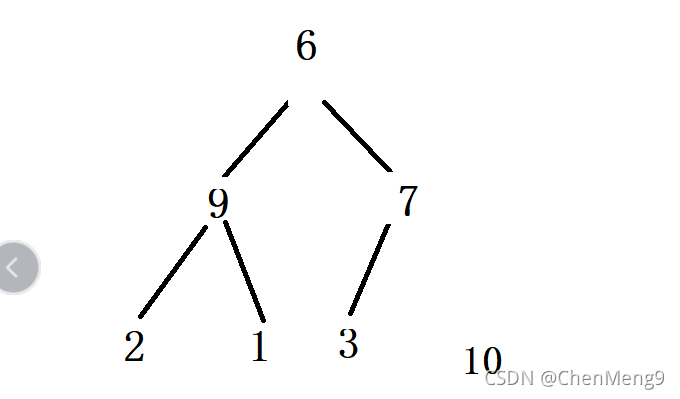
这样保证我们得到最大的数,并放在末尾,然后在调整一次 ,因为我们已经初始调整过大顶堆,所以此时只有第一个数不稳定 ,从上往下调整 ,判断左右孩子的大小,用大的数在和顶端的数进行判断,直到顶端的数放到合适位置。然后在次交换第一个数和最后一个数 ,重复上述操作,直到剩一个数。
父结点到子节点的距离 j = 2i+1 , 子节点到父节点的距离 i = (j-1)/2
代码的思想 :初始先把函数整体调整成大顶堆 ,然后在循环中进行交换和在次调整。
void AdjustHeap(int* arr, int start, int end) //调整大顶堆的函数
{
int tmp = arr[start];
int i=start; //i为父节点
int j = 2*i+1; //j为父节点的左孩子
for (i = start; j <=end;j = 2*i + 1)
{
if (j<end && arr[j] < arr[j + 1]) //如果右孩子大于左孩子 ,让j等于右孩子
{
j++;
}
if (arr[j]>arr[i]) 如果孩子大于父节点,就进行交换
{
arr[i] = arr[j];
i = j;
}
else
{
break;
}
}
arr[i] = tmp; //这时i就在合适的位置
}
void HeapSort(int* arr, int len)
{
for (int i = (len - 2) / 2; i >= 0; i--) //i值是最后一个结点的父节点
{
AdjustHeap(arr, i, len - 1);
}
for (int i=0;i<len-1;i++)
{
int tmp = arr[0];
arr[0] =arr[len-i-1];
arr[len - i - 1] = tmp; 每次找到最大的值和末尾进行交换,然后舍掉末尾
AdjustHeap(arr, 0, len - i - 1-1);
}
}
快速排序:
时间复杂度O(nlogn) 空间复杂度O(logn) 稳定性:不稳定
快速排序是在数组中找一个基准值 ,将数组中小于基准值的值放在左边 ,将数组大于基准值的值放在右边,然后将左边那组数单独拿出来在次进行快排 ,将右边那组拿出来进行快排 ,最后直到基准值的左右两边都小于两个数时停止
代码思想 : 开始我们定义一个left指向头,right指向尾 , 然后将left的值拿出来作为基准值 ,先和right进行比较 ,如果right大于基准值 就向左走 ,如果小于就让left等于right的值,如果让left向右走,如果left大于基准值 ,就让right等于left 的值,这样依次直到left等于right,走完一个数组,如果用递归的思想传左边那组和右边那组在进行循环 。 总之就是在左边找大的值,在右边找小的值。
void QuickSort(int* arr, int len,int left,int right)
{
int start = left; //因为底下right和left都是变的,为了方便判断是否递归,标记一下传进来的左右边界 。
int end = right;
int tmp = arr[left]; //tmp就是所选基准值
while (left < right)
{
while (left < right && arr[right] >= tmp) //在右边找小的值
{
right--;
}
if (left == right) break;
arr[left] = arr[right];
while (left < right && arr[left] < tmp) //在左边找大的值
{
left++;
}
if (left == right) break;
arr[right] = arr[left];
}
arr[left] = tmp;
if (start<left-1) //如果左边的数大于两个
{
QuickSort(arr, len, 0, left - 1);
}
if (end>right+1) //如果右边的数大于两个
{
QuickSort(arr, len, right + 1, len - 1);
}
}





 本文详细介绍了堆排序和快速排序两种高效的排序算法。堆排序通过构建并调整大顶堆来实现元素排序,时间复杂度为O(nlogn),空间复杂度为O(1)。快速排序则选取基准值对数组进行划分,递归地对子数组进行排序,平均时间复杂度为O(nlogn),空间复杂度为O(logn)。
本文详细介绍了堆排序和快速排序两种高效的排序算法。堆排序通过构建并调整大顶堆来实现元素排序,时间复杂度为O(nlogn),空间复杂度为O(1)。快速排序则选取基准值对数组进行划分,递归地对子数组进行排序,平均时间复杂度为O(nlogn),空间复杂度为O(logn)。
















 621
621

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








