从0开始学习机器学习--Day2--梯度下降及其在线性回归的应用

原创

已于 2024-10-29 21:29:33 修改 · 1k 阅读

·

15

·

CC 4.0 BY-SA版权

版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。

文章标签：

#学习 #机器学习 #人工智能

于 2024-10-22 22:15:56 首次发布

在上一篇文章中初步地了解了机器学习的一些概念并接触了代价函数的数学定义，今天从代价函数开始继续学习机器学习

代价函数（cost function）

代价函数 $J(\theta _0,\theta_1)= \frac{1}{2m}\sum_{1}^{m}{(h(x^{i})-y^{i})}^{2}$

为了更好地让代价函数J可视化，令 $\theta_0 = 0$ ，从而获得代价函数 $h_\theta(x) = \theta_1x$

取一个只有（1,1）（2,2）（3,3）训练集，当 $\theta_1$ 分别取到1、0.5、0时，代价函数的输出值为0、0.58、2.3，若是把 $\theta_1$ 能取到的所有值对应的代价函数值画出来，我们能观察到 $J(\theta)$ 的形状像二次函数，而当 $\theta_1$ 取到1时代价函数的值最小且为0。而学习算法的目标，就是通过选择 $\theta_1$ 的值来获得最小的 $J(\theta_1)$ 。

但如果 $\theta_0$ 不为0，例如取到50，并且取 $\theta_1$ 为0.06，代价函数 $J (\theta_0,\theta_1)$ 的图像如下图：

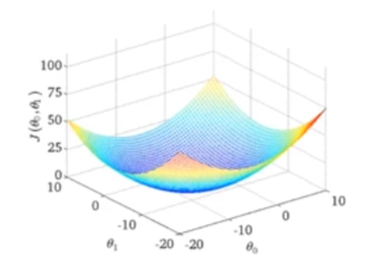
代价函数三维碗状图

曲面的高度就是代价函数的值，水平方向上的点的高度都是一致的，用等高图来表示可以更清晰地看到：

最低0.47元/天解锁文章

评论

被折叠的条评论为什么被折叠?

到【灌水乐园】发言

查看更多评论

添加红包

成就一亿技术人!

hope_wisdom

发出的红包

实付元

使用余额支付

点击重新获取

扫码支付

钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。