第四章 决策树
1 基本流程
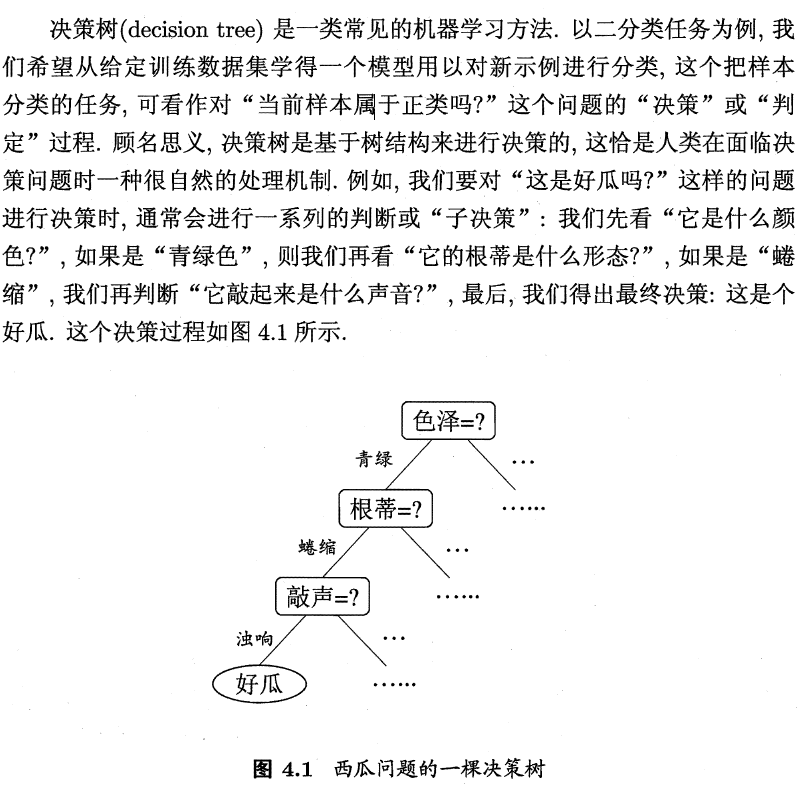
2 划分选择
随着划分过程不断进行,我们希望决策树的分支节点所包含的样本尽可能属于同一类别,即结点的“纯度”(purity)越来越高。
2.1 信息增益
2.1.1 什么是信息熵
https://www.zhihu.com/question/22178202
什么是熵:一种事物的不确定性。
信息:消除不确定性的事物。
信息的功能:调整概率;排除干扰;确定情况(比如卖瓜的人说了一句,包熟包甜)。
噪音:不能消除某人对某件事情不确定性的事物。
数据 = 信息 + 噪音
2.1.2 熵如何量化——等概率
参照某个不确定事件作为单位,如抛一次硬币记为1bit。
如8个等概率的不确定情况,相当于抛3次硬币,即2^3个可能情况,熵为3bit。
如10个等概率的不确定情况,相当于抛log10次硬币,即2^log10个可能情况,熵为log10bit,该对数以2为底。
2.1.3 熵如何量化——概率不等
计算公式:

2.1.4 信息如何量化
得知信息前后,熵的差额。

信息前熵:log4 = 2
信息后熵:31/6log6 + 1/2*log2
2.1.5 小结

2.1.6 例子
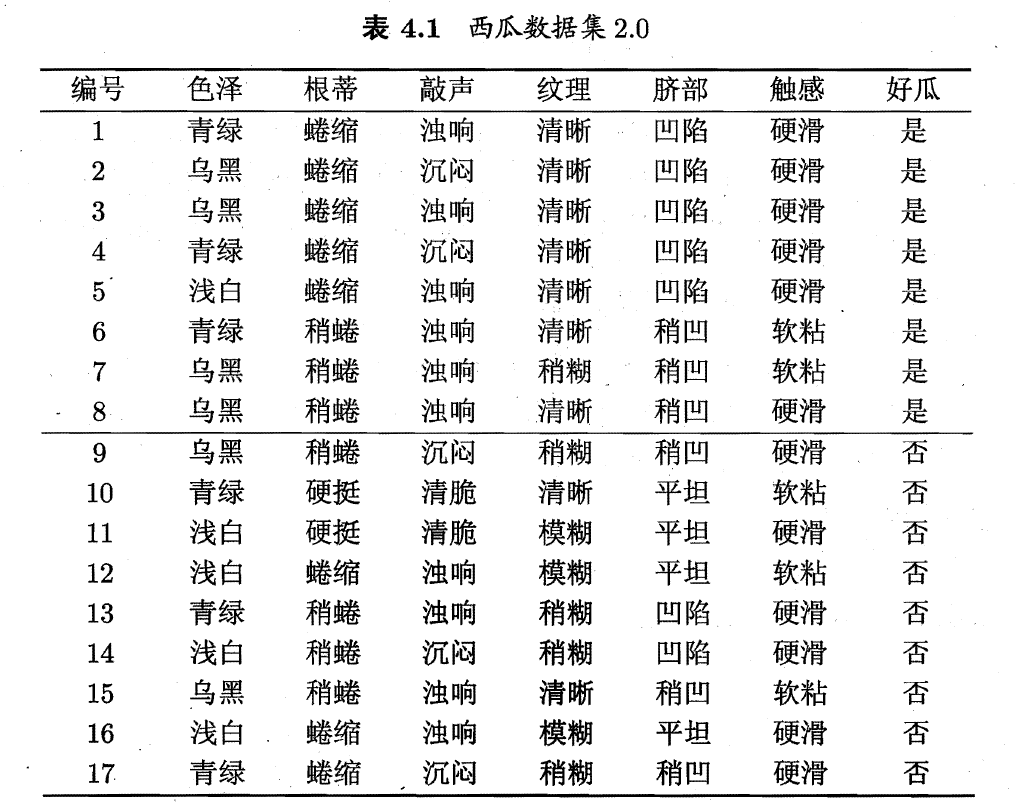
#计算色泽属性的信息增益
import numpy as np
#根据好坏瓜比例计算根结点信息熵
Good = 8
Bad = 9
Total = 17
EntD = - 8/17 * np.log2(8/17) - 9/17 * np.log2(9/17)
#计算色泽的信息
#计算各色瓜中,好坏瓜的数量
Green_good = 3
Green_bad = 3
Black_good = 4
Black_bad = 2
White_good = 1
White_bad = 4
#计算各色瓜中,好坏瓜出现概率
P_Green_good = 3/6
P_Green_bad = 3/6
P_Green = 6/17
P_Black_good = 4/6
P_Black_bad = 2/6
P_Black = 6/17
P_White_good = 1 /5
P_White_bad = 4/5
P_White = 5/17
#计算色泽各分支节点的信息熵
EntD_Green = -P_Green_good*np.log2(P_Green_good) -P_Green_bad*np.log2(P_Green_bad)
EntD_White = -P_White_good*np.log2(P_White_good) -P_White_bad*np.log2(P_White_bad)
EntD_Black = -P_Black_good*np.log2(P_Black_good) -P_Black_bad*np.log2(P_Black_bad)
#加权得色泽属性的信息熵
EntD_color = P_Green*EntD_Green + P_White*EntD_White + P_Black*EntD_Black
#相减得色泽属性的信息增益
Gain = EntD - EntD_color
Gain
0.10812516526536531
根据上述类似的做法,计算得不同属性得信息增益。
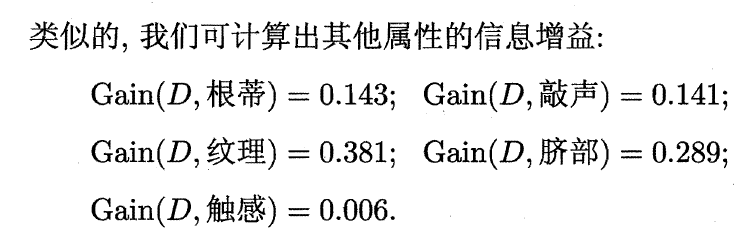
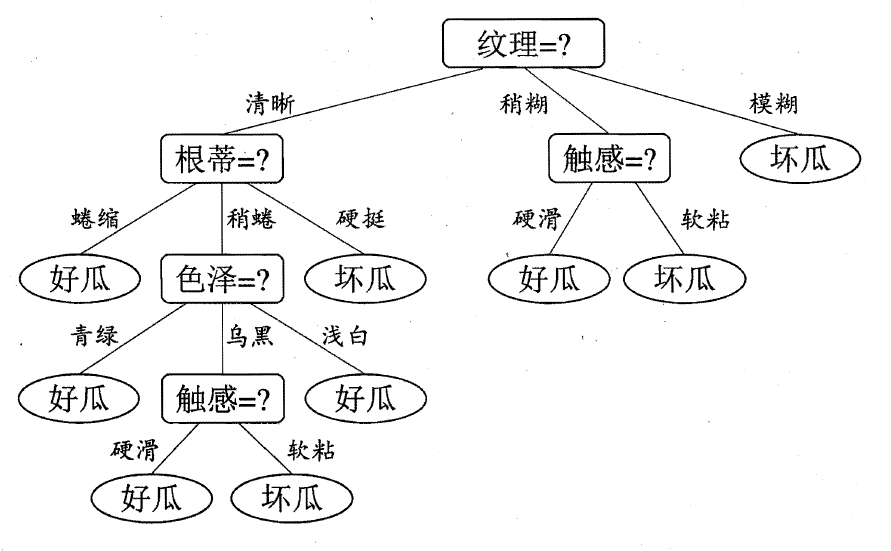
根据信息增益最大的属性—纹理,对根节点进行划分
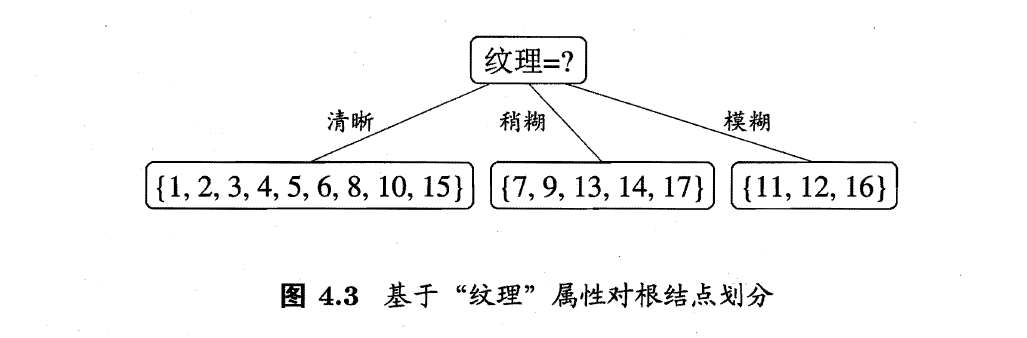
基于已知纹理类别,计算各属性的信息增益,得到决策树。
2.2 增益率
信息增益准则对可取值数目较多的属性有所偏好。
为解决该问题,Quinlan(1993)使用增益率(gain ratio)选择最优划分属性,定义如下:

先从候选划分属性中找出信息增益高于平均水平属性,再从中选择增益率最高的属性划分决策数。
2.3 基尼指数
2.3.1 分类树:基尼指数最小准则。
数据集基尼指数:

属性基尼指数:

例子
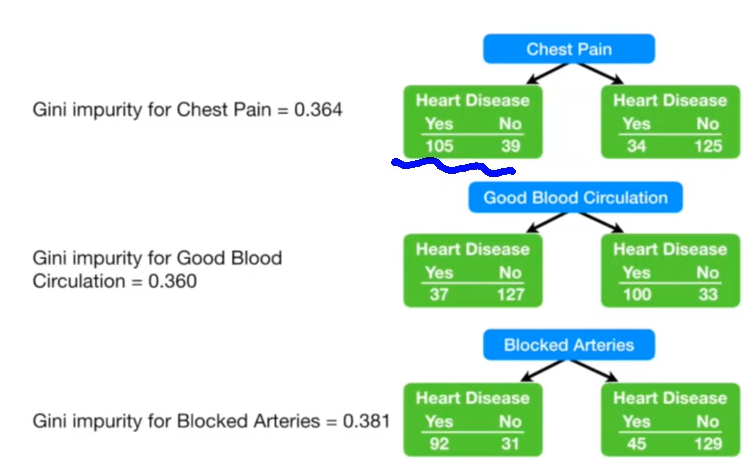
#数据集基尼指数:两分叉为例
def gini_index_single(a,b):
single_gini = 1 - ((a/(a+b))**2) - ((b/(a+b))**2)
return single_gini
print(gini_index_single(105,39),gini_index_single(130,14))
#由此可见,纯度越高,基尼指数越小
0.3949652777777779 0.17554012345679013
#属性基尼指数:数据集的加权
def gini_index(a, b, c, d):
zuo = gini_index_single(a,b)
you = gini_index_single(c,d)
gini_index = zuo*((a+b)/(a+b+c+d)) + you*((c+d)/(a+b+c+d))
return gini_index
gini_index(105, 39, 34, 125)
0.36413900824044665
gini_index(37, 127, 100, 33)
0.3600300949466547
gini_index(92, 31, 45, 129)
0.38080175646758213
选择基尼指数最小的属性做第一次分叉,即good blood circulation
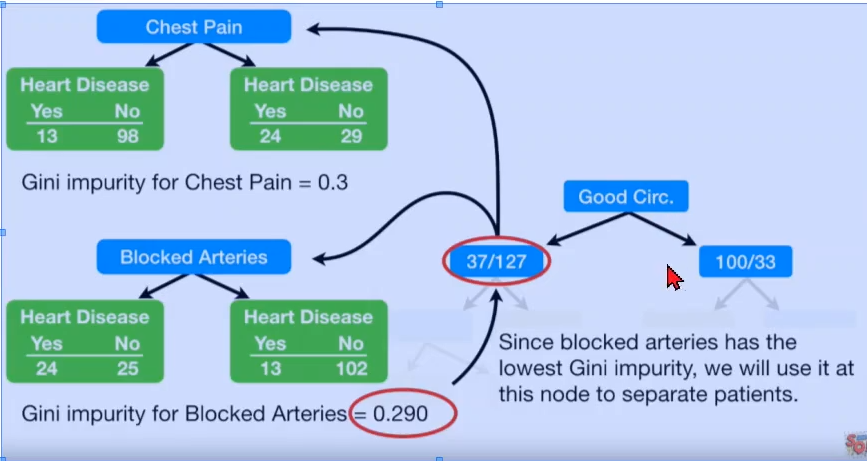
继续进行第二次分叉
gini_index_single(37,127)
0.3494199881023201
gini_index(13, 98, 24, 29)
0.30011649938019014
gini_index(24, 25, 13, 102)
0.2899430822169802
根据上图,Blocked arteries的Gini impurity为0.29,优于chest pain。(基尼指数越小越好)
且分叉后的基尼指数低于0.34,因此应当进行第二次分叉
因此以Blocked arteries为第二次分叉属性。得到:
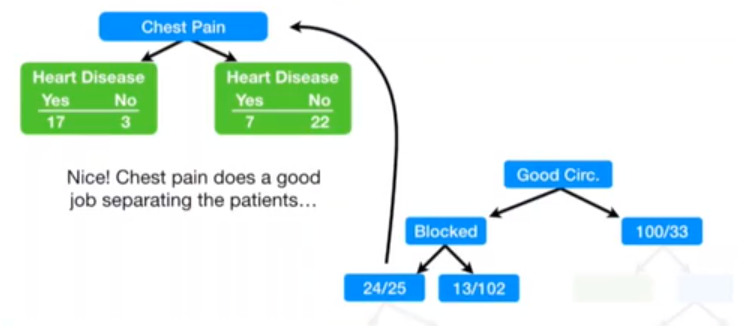
gini_index_single(24, 25)
0.4997917534360683
gini_index(17,3,7,22)
0.3208304011259677
由于0.32<0.49,因此应当进行第三次分叉。
最终分叉结果如下:
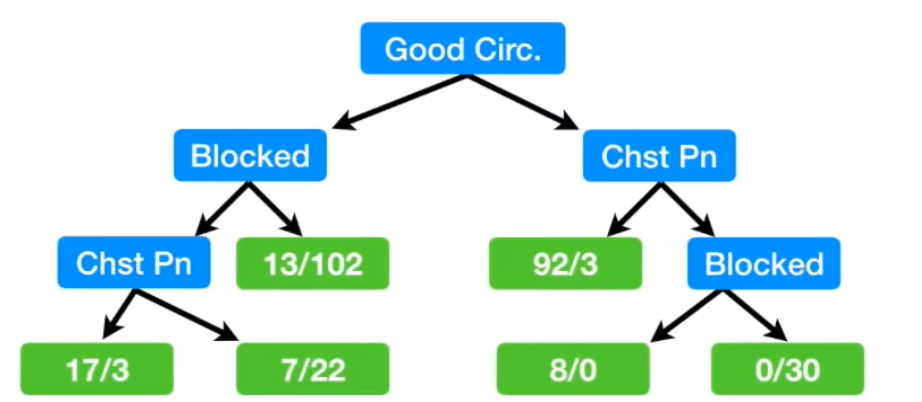





 本文介绍了决策树的基本流程,重点讲解了信息熵、信息增益、增益率和基尼指数的概念及其在决策树划分过程中的应用。通过实例展示了如何计算这些指标,并用于选择最优划分属性。最后提到了信息增益可能对多值属性的偏好以及如何通过增益率来平衡这一问题。
本文介绍了决策树的基本流程,重点讲解了信息熵、信息增益、增益率和基尼指数的概念及其在决策树划分过程中的应用。通过实例展示了如何计算这些指标,并用于选择最优划分属性。最后提到了信息增益可能对多值属性的偏好以及如何通过增益率来平衡这一问题。

















 498
498

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








