【剑指Offer学习】【题23：二叉搜索树的后序遍历序列】

最新推荐文章于 2024-05-27 21:18:06 发布

原创最新推荐文章于 2024-05-27 21:18:06 发布 · 151 阅读

0 ·

CC 4.0 BY-SA版权

文章标签：

#Java #面试题

剑指offer 专栏收录该内容

52 篇文章

订阅专栏

本文介绍了一种算法，用于判断给定的整数数组是否为二叉搜索树的后序遍历结果。通过递归地检查数组元素与根节点的关系，确保所有左子树节点小于根节点，所有右子树节点大于根节点。

题目：
输入一个整数数组，判断该数组是不是某二叉搜索树的后序遍历的结果。如果是则输出Yes,否则输出No。假设输入的数组的任意两个数字都互不相同。

思路：
二叉搜索树：左结节比根结节小，右结节比根结节大。
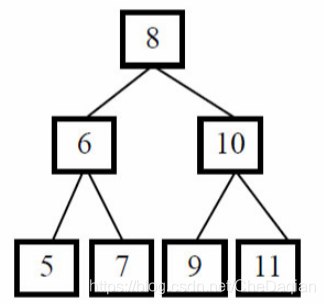
在这里插入图片描述
在{5，7，6，9，11，10，8}中，后续遍历的结果的最后一个数字8是根结点的值。前3个数5、7、6都比8小，是值为8根节点的左子树的结点；后3个数9，11，10都比8大，是值为8根节点的右子树的结点。
1、取数列的最后一个数字为根节点；
2、找到左右子树的分界坐标，并采用递归的方式分别进行二叉搜索树判断；

程序：

public class subject23 {
	public static boolean VerifySquenceOfBST(int[] sequence) {
		if(sequence.length == 0 || sequence == null) {
			return false;
		}
		return VerifySquenceOfBST(sequence, 0, sequence.length - 1);
	}
	public static boolean VerifySquenceOfBST(int[] sequence, int start, int end) {
		if(start >= end) 
			return true;
		int root = sequence[end];//取序列最后一个数值为根节点
		int i = start;
		for( ; i < end; i ++) {
			//如果大于节点，则直接break,记录下左子树和右子树的分界坐标
			if(sequence[i] > root)
				break;
		}
		for(int j = i; j < end; j ++) {
			if(sequence[j] < root) {
				return false;//右结节的值大于根结节的值
			}
		}
		return VerifySquenceOfBST(sequence, start, i - 1) && VerifySquenceOfBST(sequence, i, end - 1);
	}
	public static void main(String args[]) {
		int[] a = {5,7,6,9,11,10,8};
		int[] b = {7,4,6,5};
		System.out.println(VerifySquenceOfBST(a));
		System.out.println(VerifySquenceOfBST(b));
	}
}