【乘积最大】

题目描述

乘积最大
给定 N 个整数 A1, A2,…A_NA
1
​
,A
2
​
,⋯A
N
​
。请你从中选出 KK 个数，使其乘积最大。

请你求出最大的乘积，由于乘积可能超出整型范围，你只需输出乘积除以 10^9+910
9
+9 的余数。

注意，如果 X<0X<0，我们定义 XX 除以 10^9+910
9
+9 的余数是负(-X)(−X)除以 10^9+910
9
+9 的余数。

即：0-((0-x) % 10^9+9)0−((0−x)%10
9
+9)。

输入描述
输入格式：

第一行包含两个整数 N,KN,K。

以下 NN 行每行一个整数 A_iA
i
​
。

其中，1 \leq K \leq N \leq 10^5， -10^5 \leq A_i \leq 10^51≤K≤N≤10
5
，−10
5
≤A
i
​
≤10
5
。

输出描述
输出一个整数，表示答案。

输入输出样例
示例
输入

5 3
-100000
-10000
2
100000
10000

输出

999100009

copy
运行限制
最大运行时间：1s
最大运行内存: 256M

方法1

容易想到使用动态规划的二维数组dp[i][j]，表示从前i个选出j个使得乘积最大，但超时
状态方程如下：

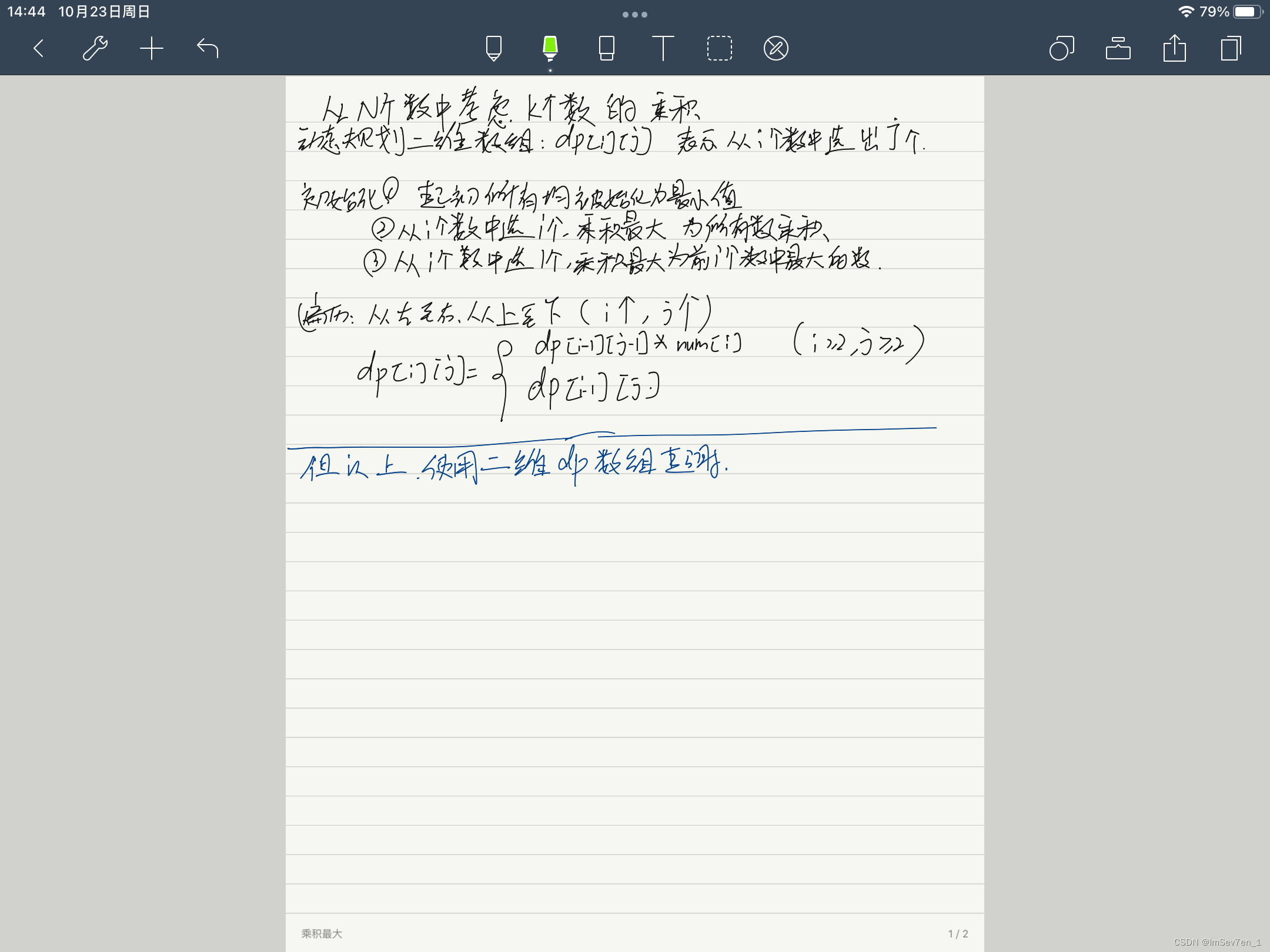
代码：

#include <iostream>
long long  MIN=-1e9;
using namespace std;
long long MOD = 1e9 + 9;
const long long MAXN = 1e4 + 10;

//避免溢出，定义为全局变量
long long nums[MAXN];
long long dp[MAXN][MAXN];
int main() {
    //long long temp;
    long long N, K;
    cin >> N >> K;
    for (long long i = 1; i <= N; i++) {
        cin >> nums[i];
    }

    //初始化
    for (int i = 0; i <= N; i++) {
        for (int j = 0; j <= N; j++) {
            dp[i][j] = MIN;
        }
    }
    for (long long i = 1; i <= N; i++) {//从前i个中选1个
        for (long long j = 1; j <= i; j++) {
            dp[i][1] = max(dp[i][1], nums[j]);
        }
    }
    for (long long i = 1; i <= N; i++) {
        long long sum = 1;
        for (long long j = 1; j <= i; j++) {
            sum *= nums[j];
        }
        dp[i][i] = sum;
    }

    //从左至右，从上至下遍历
    for (int i = 3; i <= N; i++) {
        for (int j = 2; j < i; j++) {
            dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - 1] * nums[i]);
        }
    }
    if(dp[N][K]>=0){
      cout << dp[N][K] % MOD << endl;
    }
    else{
      cout<<0-((0-dp[N][K]%MOD))<<endl;
    }
    
    return 0;
}

方法2

使得K个乘积最大，我们可以对K的奇偶性入手，并使用类似于双指针做法实现。
分析如下：

代码：

#include <iostream>
#include <vector>
#include<algorithm>
using namespace std;

long long MOD=1e9+9;
int main(){
    long long N,K;
    vector<long long> nums;
    long long temps;
    long long ans=1;
    int flag=1;//判断是否全为负数
    long long left,right;//双指针
    cin>>N>>K;
    for(int i=0;i<N;i++){
        cin>>temps;
        nums.push_back(temps);
    }
    sort(nums.begin(),nums.end());
    //判断奇偶
    if(K%2){//K为奇数,先取一个最大的转换为偶数的情形
        ans=nums[N-1];
        if(ans<0){//全为负数
            flag=0;
        }
        --K;
        --N;
    }
    
    left=0;
    right=N-1;//坑
    while(K){
        long long leftMulti=nums[left]*nums[left+1];//一定要先取余数
        long long rightMulti=nums[right]*nums[right-1];
        if(flag){//并不全为负数
            if(leftMulti>rightMulti){
                ans=leftMulti%MOD*ans%MOD;
                left+=2;
                
            }
            else{
                ans=rightMulti%MOD*ans%MOD;
                right-=2;
            }
        }
        else{//全为负数
            ans=rightMulti%MOD*ans%MOD;//使得拿去一个负数后,剩下的偶数个乘积尽可能小
            right-=2;
        }
        K-=2;
    }
    cout<<ans<<endl;
}