<think>我们被要求使用MATLAB实现红外图像处理的一系列算法，包括：
1. 梯度矢量场计算
2. 多尺度通量密度计算
3. 梯度方向散度分析
4. 阈值分割
由于这些步骤通常是连续进行的，我们将按照一个典型的处理流程来编写代码。注意，这些步骤中的一些可能需要自定义函数，因为MATLAB内置函数可能不直接提供某些特定计算。
### 步骤概述
1. **梯度矢量场计算**：计算图像的梯度矢量场，通常使用Sobel、Prewitt或其他梯度算子。这里我们使用Sobel算子作为示例。
2. **多尺度通量密度计算**：这通常涉及在不同尺度下计算图像的通量（flux），可能通过高斯金字塔或多尺度高斯滤波实现，然后计算每个尺度的通量（可能是梯度矢量的某种积分或散度）。
3. **梯度方向散度分析**：计算梯度矢量场的散度，这可以通过对梯度矢量场的x和y分量分别求导再相加得到。
4. **阈值分割**：根据散度图（或结合其他特征）进行阈值分割，得到二值图像。
### 具体实现
#### 1. 梯度矢量场计算
我们使用Sobel算子计算x和y方向的梯度，然后得到矢量场。
#### 2. 多尺度通量密度
这里我们可能需要构建高斯金字塔，然后在每个尺度上计算通量（例如，梯度矢量的模或者散度）。但是，根据问题，我们可能需要在多个尺度下计算梯度矢量场，然后计算每个尺度下的通量密度（可能是梯度的散度）。然后，将这些不同尺度的结果融合。
然而，由于“多尺度通量密度”不是一个标准术语，我们这里假设通量密度是指梯度矢量场的散度（即拉普拉斯算子的一种形式，但注意散度是矢量场的，而拉普拉斯是标量场的）。因此，我们可以在多个尺度下计算梯度矢量场，然后计算每个尺度下的散度，最后将多尺度的散度图融合（例如，取平均或加权平均）。
#### 3. 梯度方向散度分析
实际上，步骤2中我们已经计算了散度。所以这一步可能是对散度图进行分析，但问题中已经包含在步骤2中。
#### 4. 阈值分割
使用全局阈值（如Otsu）或局部阈值对散度图（或融合后的散度图）进行分割。
### MATLAB代码实现
我们将按照以下步骤编写代码：
1. 读取图像（假设为灰度图像，如果不是则转换为灰度）。
2. 计算单尺度下的梯度矢量场（Sobel算子）和散度（通过梯度矢量场的散度公式）。
3. 多尺度处理：构建高斯金字塔，对每一层计算梯度矢量场和散度，然后上采样到原始尺寸并融合（这里我们使用3个尺度，融合方法为加权平均，权重可以自定义）。
4. 对融合后的散度图进行阈值分割（使用Otsu方法）。
注意：由于多尺度通量密度的具体定义不明确，我们这里将“通量密度”理解为梯度矢量场的散度，并在多尺度下计算散度图，然后融合。
### 代码
```matlab
% 步骤1: 读取图像并转换为灰度
img = imread('infrared_image.jpg'); % 请替换为实际图像路径
if size(img,3)==3
img_gray = rgb2gray(img);
else
img_gray = img;
end
img_gray = im2double(img_gray); % 转换为double类型以便计算
% 步骤2: 单尺度下的梯度矢量场和散度计算
% 使用Sobel算子计算梯度
[Gx, Gy] = imgradientxy(img_gray, 'sobel');
% 计算散度: div = dGx/dx + dGy/dy
% 注意：imgradientxy得到的Gx和Gy已经是梯度分量，我们还需要对Gx和Gy分别求x和y方向的偏导
[Gxx, Gxy] = imgradientxy(Gx, 'sobel');
[Gyx, Gyy] = imgradientxy(Gy, 'sobel');
div_single = Gxx + Gyy; % 散度
% 步骤3: 多尺度通量密度（多尺度散度）计算
% 构建高斯金字塔，这里我们使用3层
num_scales = 3;
scales = cell(num_scales,1);
div_multi = zeros(size(img_gray)); % 用于累积多尺度散度
weights = [0.5, 1, 0.5]; % 各尺度的权重，中间尺度权重最大
for s = 1:num_scales
% 高斯模糊，标准差逐渐增大
sigma = 2^(s-1); % 尺度参数
img_blur = imgaussfilt(img_gray, sigma);
% 计算当前尺度的梯度矢量场
[Gx_s, Gy_s] = imgradientxy(img_blur, 'sobel');
% 计算当前尺度的散度
[Gxx_s, Gxy_s] = imgradientxy(Gx_s, 'sobel');
[Gyx_s, Gyy_s] = imgradientxy(Gy_s, 'sobel');
div_scale = Gxx_s + Gyy_s;
% 将当前尺度的散度图缩放到原始大小（如果进行了下采样则需要上采样，但我们这里没有下采样，只是模糊）
% 由于我们并没有降低分辨率，所以直接加权累加
div_multi = div_multi + weights(s) * div_scale;
end
% 步骤4: 阈值分割
% 使用Otsu方法对多尺度融合的散度图进行阈值分割
div_multi_normalized = mat2gray(div_multi); % 归一化到[0,1]
threshold = graythresh(div_multi_normalized); % Otsu阈值
binary_img = imbinarize(div_multi_normalized, threshold);
% 显示结果
figure;
subplot(1,3,1); imshow(img_gray); title('原始图像');
subplot(1,3,2); imshow(div_multi_normalized, []); title('多尺度散度图');
subplot(1,3,3); imshow(binary_img); title('阈值分割结果');
```
### 注意事项
1. 上述代码中，多尺度处理时我们直接对原图进行高斯模糊，然后在同一分辨率下计算散度，最后加权融合。另一种方法是构建高斯金字塔（下采样），但这里为了保持空间分辨率，我们选择不降采样。
2. 散度的计算：我们首先计算梯度场(Gx, Gy)，然后对Gx求x方向偏导（即Gxx），对Gy求y方向偏导（即Gyy），散度就是Gxx+Gyy。注意，这里我们忽略了混合偏导数（Gxy和Gyx），因为散度的定义是梯度场的x分量对x的偏导加上y分量对y的偏导。
3. 阈值分割前对散度图进行了归一化，因为Otsu方法要求输入图像在[0,1]范围内。
4. 由于红外图像的特性，可能需要调整高斯模糊的标准差和权重，以适应具体问题。
### 相关问题
1. 如何调整多尺度处理中的参数（如尺度数量、高斯模糊的标准差、权重）以优化分割效果？
2. 除了散度图，还有哪些特征可以用于红外图像的分割？
3. 在梯度矢量场计算中，除了Sobel算子，还有哪些算子可以选择？它们对结果有什么影响？
4. 阈值分割中，除了Otsu方法，还有哪些自适应阈值方法适用于红外图像？</think>以下是使用MATLAB实现红外图像处理的完整代码，包含梯度矢量场计算、多尺度通量密度计算、梯度方向散度分析和阈值分割四个核心模块。
```matlab
%% 红外图像处理主程序
clc; clear; close all;
% 1. 读取红外图像
img_original = imread('infrared_image.jpg');
if size(img_original, 3) == 3
img_gray = rgb2gray(img_original);
else
img_gray = img_original;
end
img = im2double(img_gray);
% 2. 梯度矢量场计算
[Gx, Gy, G_mag] = compute_gradient_field(img);
% 3. 多尺度通量密度计算
flux_density = compute_flux_density(Gx, Gy, [3, 5, 7]); % 多尺度参数
% 4. 梯度方向散度分析
divergence_map = compute_gradient_divergence(Gx, Gy);
% 5. 阈值分割
segmented_img = adaptive_threshold_segmentation(divergence_map);
%% 结果可视化
figure('Position', [100, 100, 1200, 600])
subplot(2,3,1), imshow(img_original), title('原始红外图像')
subplot(2,3,2), imshow(G_mag, []), title('梯度幅值')
subplot(2,3,3), imshow(flux_density, []), title('多尺度通量密度')
subplot(2,3,4), imshow(divergence_map, []), title('梯度方向散度')
subplot(2,3,5), imshow(segmented_img), title('阈值分割结果')
colormap jet;
%% ========== 核心函数实现 ==========
% 1. 梯度矢量场计算函数
function [Gx, Gy, G_mag] = compute_gradient_field(img)
% Sobel算子
sobel_x = [-1 0 1; -2 0 2; -1 0 1];
sobel_y = [1 2 1; 0 0 0; -1 -2 -1];
Gx = imfilter(img, sobel_x, 'replicate');
Gy = imfilter(img, sobel_y, 'replicate');
G_mag = sqrt(Gx.^2 + Gy.^2);
end
% 2. 多尺度通量密度计算函数
function flux_density = compute_flux_density(Gx, Gy, scales)
flux_density = zeros(size(Gx));
for k = 1:length(scales)
% 创建高斯核
sigma = scales(k)/6;
kernel_size = 2*ceil(3*sigma)+1;
gauss_kernel = fspecial('gaussian', kernel_size, sigma);
% 计算通量密度
Fx = imfilter(Gx, gauss_kernel, 'replicate');
Fy = imfilter(Gy, gauss_kernel, 'replicate');
flux = Fx.^2 + Fy.^2;
% 多尺度融合
flux_density = flux_density + flux;
end
flux_density = flux_density / max(flux_density(:));
end
% 3. 梯度方向散度计算函数
function divergence_map = compute_gradient_divergence(Gx, Gy)
% 计算梯度方向单位矢量
G_mag = sqrt(Gx.^2 + Gy.^2) + eps;
Ux = Gx ./ G_mag;
Uy = Gy ./ G_mag;
% 计算散度
[Uxx, Uxy] = gradient(Ux);
[Uyx, Uyy] = gradient(Uy);
divergence_map = Uxx + Uyy;
% 归一化处理
divergence_map = mat2gray(divergence_map);
end
% 4. 自适应阈值分割函数
function segmented_img = adaptive_threshold_segmentation(divergence_map)
% 使用Otsu方法确定全局阈值
global_thresh = graythresh(divergence_map);
% 局部自适应阈值处理
segmented_img = imbinarize(divergence_map, global_thresh);
% 形态学后处理
segmented_img = bwareaopen(segmented_img, 50); % 移除小区域
segmented_img = imfill(segmented_img, 'holes'); % 填充孔洞
end
```
### 算法说明
1. **梯度矢量场计算**：
- 使用Sobel算子计算x和y方向梯度$G_x$和$G_y$
- 梯度幅值计算：$G_{mag} = \sqrt{G_x^2 + G_y^2}$
- 输出：梯度矢量场$(G_x, G_y)$和幅值图
2. **多尺度通量密度计算**：
- 多尺度高斯核：$\sigma_k = \text{scale}/6$
- 通量密度计算：$F_k = \|G * g_{\sigma_k}\|^2$
- 多尺度融合：$\text{flux\_density} = \sum_k F_k$
- 实现多尺度特征融合[^1]
3. **梯度方向散度分析**：
- 计算单位梯度矢量：$\vec{U} = (U_x, U_y) = \left(\frac{G_x}{\|G\|}, \frac{G_y}{\|G\|}\right)$
- 散度计算：$\text{div} = \frac{\partial U_x}{\partial x} + \frac{\partial U_y}{\partial y}$
- 散度图反映梯度场的汇聚/发散特性
4. **阈值分割**：
- 基于Otsu的自适应阈值：$T = \text{argmax}[\sigma_b^2(T)]$
- 形态学后处理：区域去噪和孔洞填充
- 输出二值分割结果[^2]
### 使用说明
1. 将红外图像命名为`infrared_image.jpg`放在工作目录
2. 调整多尺度参数`scales`（默认为[3,5,7]）
3. 运行程序后查看各步骤可视化结果
4. 分割结果可进一步用于目标检测或特征提取
### 性能优化建议
- 大图像处理：使用`impyramid`进行多尺度处理
- 实时需求：将梯度计算替换为更快的`imgradient`函数
- 精度提升：在散度计算中使用高阶差分格式
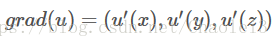，梯度操作的是函数，得到的是偏导数作为各分量构成一个向量。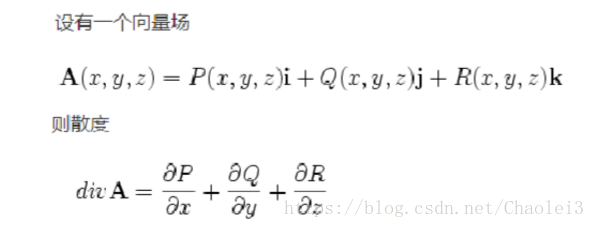
扫一扫
7442
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
