画解数据结构1.1习题线性枚举之最值算法

原创已于 2022-04-19 15:50:33 修改 · 133 阅读

0 ·

CC 4.0 BY-SA版权

文章标签：

#c语言

于 2022-04-18 23:48:11 首次发布

画解数据结构专栏收录该内容

16 篇文章

订阅专栏

本文详细介绍了线性枚举在寻找数组中三个不同最大值的最值算法，涉及遍历策略、边界更新、哈希表的应用，并特别处理了相等元素的情况。通过实例展示了如何避免重复影响结果并找到最终的最值。

线性枚举之最值算法

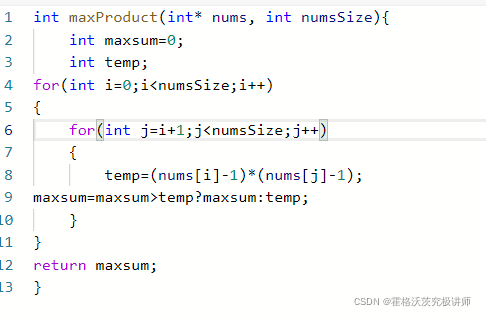
j从i+1开始遍历

二.

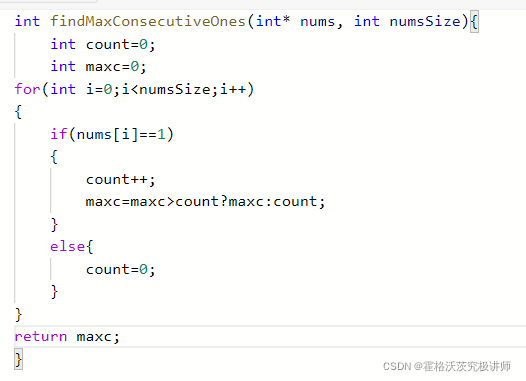
只能是1或0，是1就count++，并更新maxc，是0就将count置零

三。

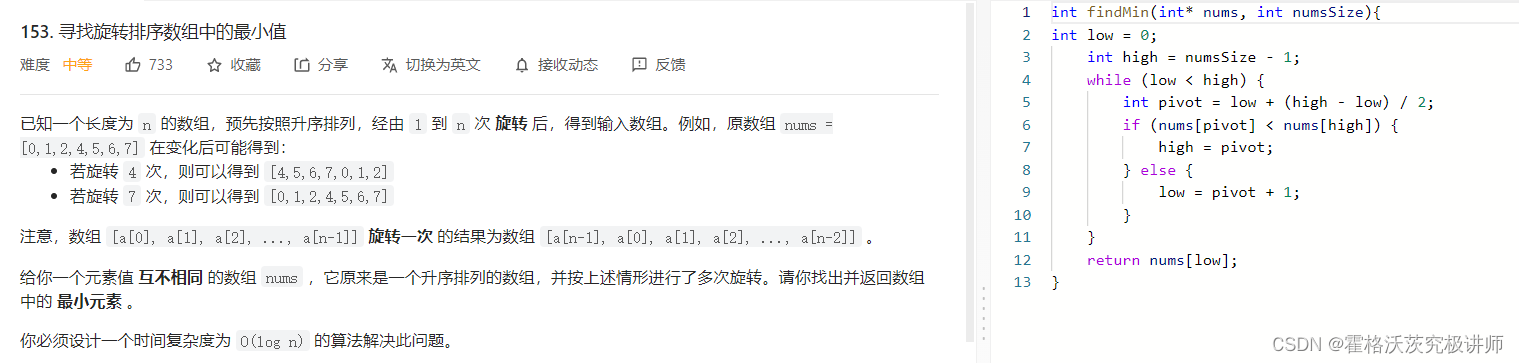
之前做过但忘得差不多了，每次取mid将其与high进行比较，>high就说明mid在最小值左边，所以更新边界

四。

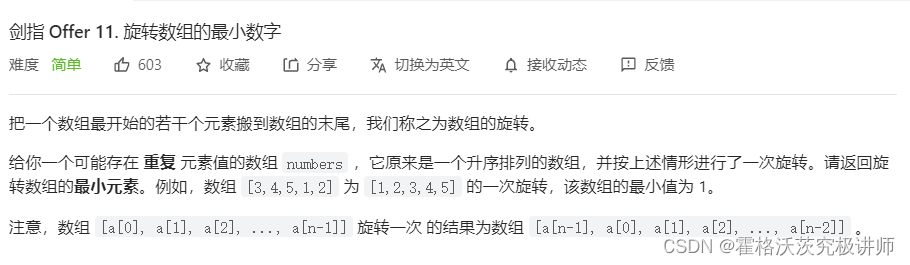
唯一区别是数组元素可以相等

所以区别是当mid与high数值相等时，无法判断最小值究竟在哪个区间，所以此时抛弃右边界，将right=right-1

五。

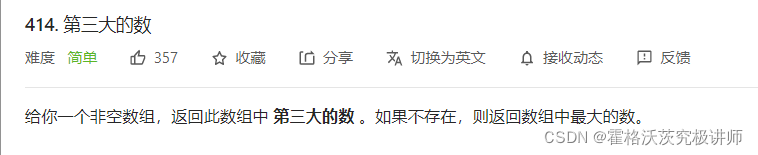
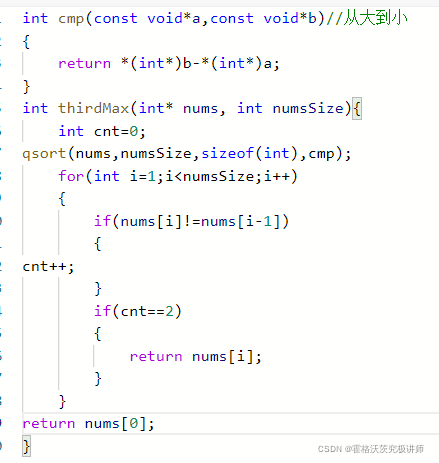
int max3=0;
    for(int i=0;i<numsSize;i++)
    {
        if(nums[i]==max1||nums[i]==max2||nums[i]==max3)
        {
            continue;
        }
        if(nums[i]>=max1)
        {
            max3=max2;
            max2=max1;
            max1=nums[i];
        }
        else if(nums[i]>=max2)
        {
            max3=max2;
            max2=nums[i];
        }
        else if(nums[i]>=max3){
            max3=nums[i];
        }
        }
    if(max3==0)
    {
        return max1;
    }
    else{
        return max3;
    }
    return 0;
}

或者一次遍历寻找max1 max2 max3

注：因为不能出现重复的数，所以当重复的数出现并影响结果（与max123）相等，直接continue

六。