画解数据结构1.1顺序表 排序 二分查找

顺序表

顺序储存，是指用一段地址连续的存储单元依次存储线性表的数据元素。

数据结构定义

length为当前数组长度

#define maxn[10000]
#define Datatype int
struct leqlist{
Datatype data[maxn];
int length;
}

2.常用接口

（1）索引：通过数组下标寻找数组元素

Datatype SeqlistIndex(struct Seqlist *sq,int i)

{return sq->data[i];}

(2)查找

Datatype SeqlistFind(struct Seqlist *sq,Datatype dt)

{

for(int i=0;i<sq->length;i++)

{
​​​​​​​if(sq->data[i]==dt)
{
return i;
}
}
return -1;
}

(3)获取长度（length）

Datatyepe SeqlistgetLength(struct Seqlist *sq)
{
return Sq->length;}

sq为结构体，直接获取结构体内变量

（3）插入

在第k个元素前插入一个数v

int Seqlistinsert{Seqlist*sq,intk,Datatype k}
{
if(sq->length==maxn)
{return 0;}
for(int i=sq->length;i>k;i--)
{sq->data[i]=sq->data[i-1];}
sq->data[k]=v;
sq->lengtg++;
return 1;}

0代表插入失败，1代表成功

（4）删除

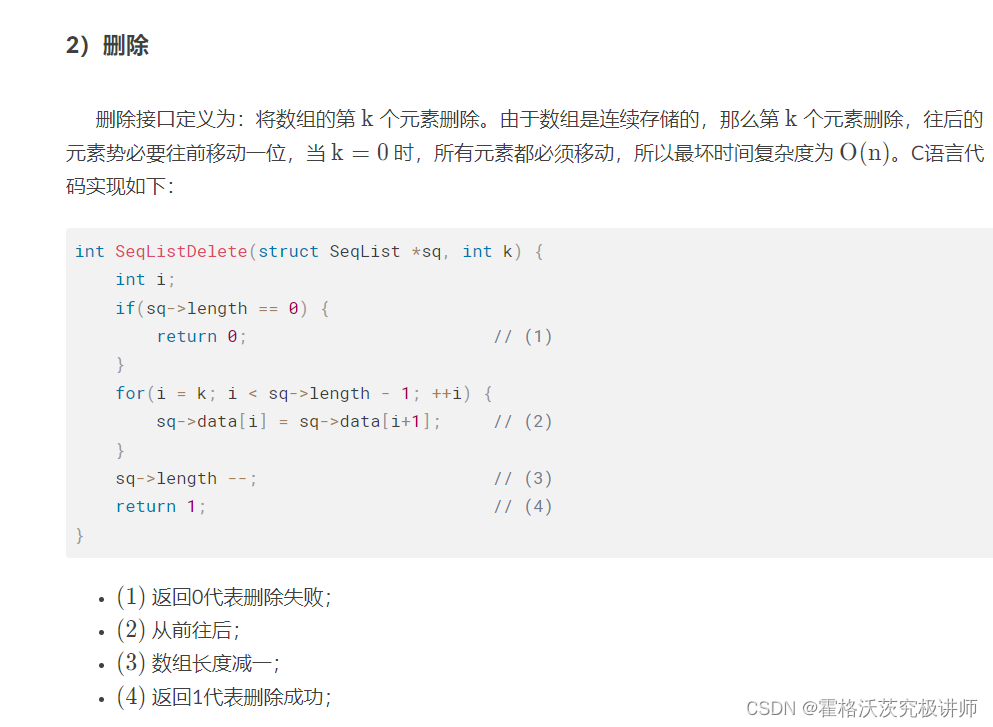
数组相关算法

1.线性枚举

普通for循环

2.前缀和差分

 int sum[maxn];

int * prem(int *nums,int*numsSize,int m,int*l,int*r)

{
for(int i=0;i<numsSize;i++)
{
sum[i]=num[i];
if(i)
{
sum[i]+=sum[i-1];
}
}
for(int i=0;i<m;i++)//m组数据
{
int leftsum=sum[l[i]];
int rightsum=sum[r[i]];
ret[i]=rightsum-leftsum;
}
return ret;
}

前缀和差分，记录1到n的实时sum，再通过输入两个边界left和right，计算left到right的差值

3.双指针

4.二分查找（用于数组有序排列时）

注意循环条件为（l<=r）

5.三分枚举

6.插入排序

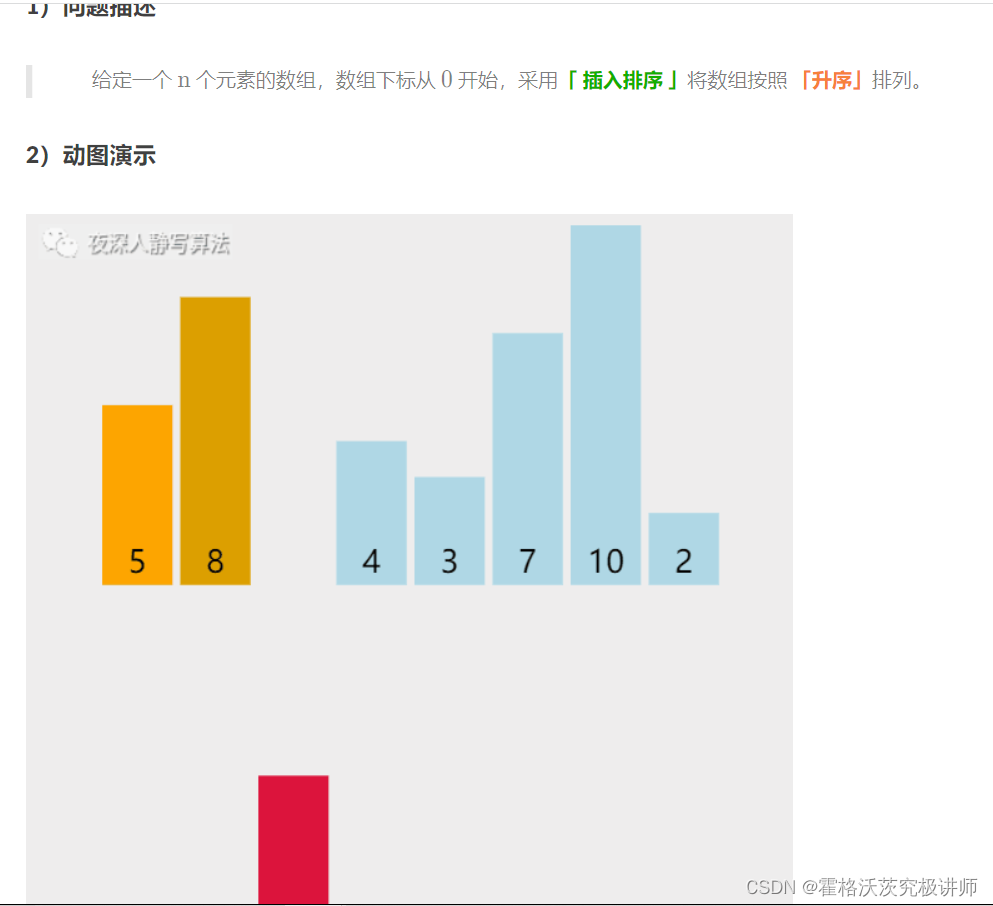
void charupaixu (int*a,int n)//n为数组长度
{
for(int i=0;i<n;i++)
{
if(i)
{
for(int j=i-1;j>=0;j--)
{
if(a[i]<=a[j])
{
a[j+1]=a[j];
}
else{
break;
a[j+1]=a[i];
}
}

7.选择排序

void xuaznepaixu(int*a,int n)
{
for(int i=0;i<n;i++)
{
int min=i;
for(int j=i;i<n;j++)
{
if(a[j]<=a[min])
{
min=j;
}
}
swap(&a[i],&a[min])
}

选择排序和插入排序的区别：

选择排序是从前往后遍历，在后面找出最小值，插入已经排好的队列后面

插入排序是从前往后遍历，为对应的i在前面已经排好的队列里面找一个合适的位置插入

8.冒泡排序

void bubblesort(int *a,intn)
{
bool swapped;
int last=n;
do
{
swapped=false;
for(int i=0;i<last-1;i++)
{
if(a[i]>a[i+1])
{
swap(&a[i],&a[i+1]);
swapped=true;
}
}
--last;
while(swapped=true)
}

每次do循环后最后一位排序好，因此--last；