3D山脉——java实现山脉模型

做这个3D山脉搞了我一下午的时间，从开始的大体构造到一步一步地解决细节问题，在此篇文章中我将一一描述我在构造山脉时遇到的问题，希望对大家有帮助

先上效果图吧

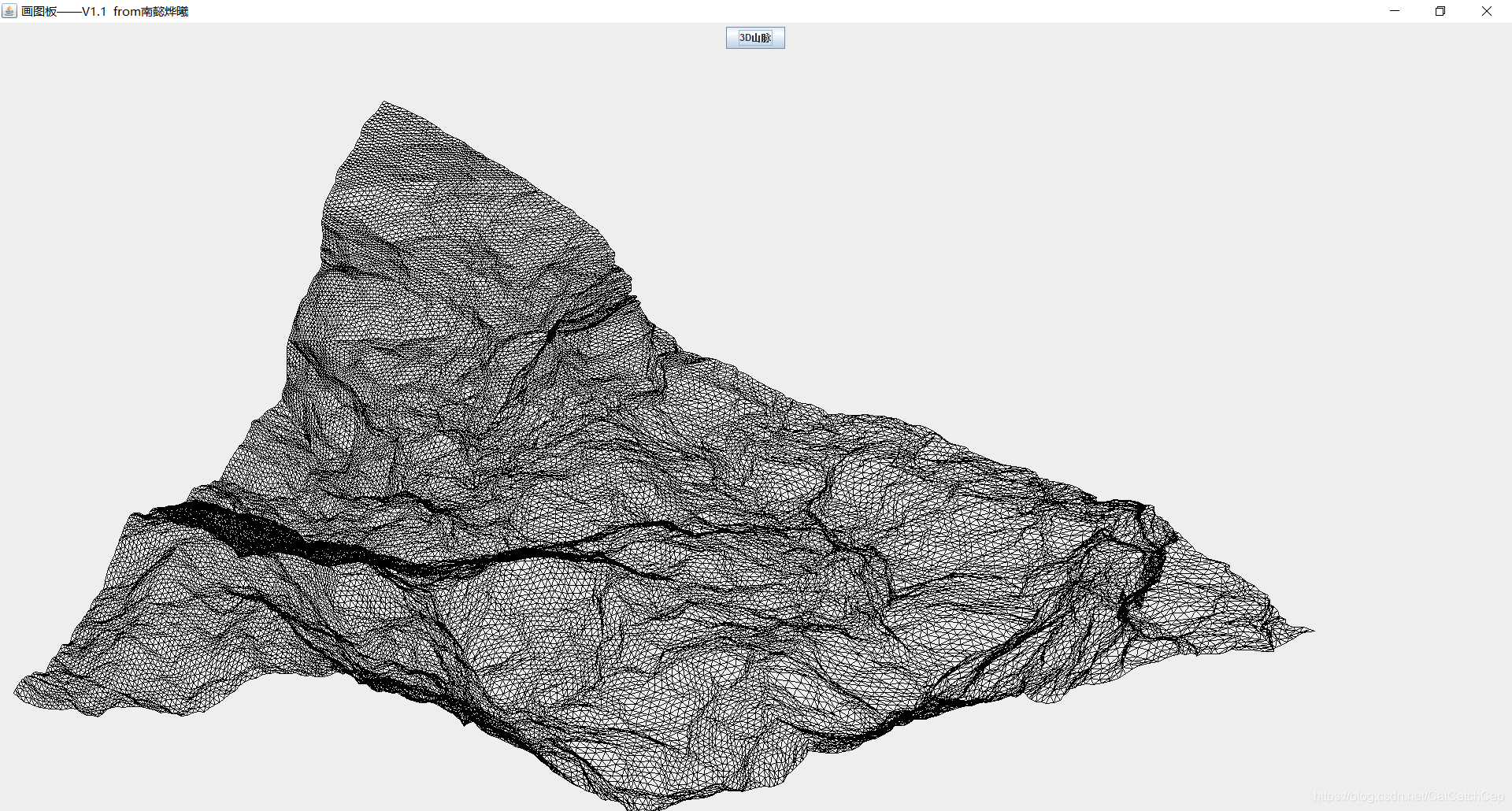
基本原理

递归，分形的灵魂
首先我们在屏幕上随机取三个点，然后每两个点取中值动荡点，再利用新产生的点画三角形，最后就能有这样的3D效果

随机取三个点

int x1=rand.nextInt(200)+480;
			int y1=rand.nextInt(200);
			int x2=rand.nextInt(300);
			int y2=rand.nextInt(100)+800;
			int x3=rand.nextInt(300)+1600;
			int y3=rand.nextInt(100)+800;

中值动荡点的生成
以一个点为例

double ranx1=(x1+x2)/k;//产生动荡值，k会随着迭代次数成倍增加
double rany1=(y1+y2)/k;
X1=(x1+x2)/2+rand.nextInt((int)ranx1*2+1)-ranx1;
Y1=(y1+y2)/2+rand.nextInt((int)rany1*2+1)-rany1;

基本点就是这样，下面我们来写这个迭代的具体方法

代码实现

我这里给出常见的错误代码，应该是最开始写这种东西都会有的错误

//参数分别为三个点的坐标，迭代层数，和震荡程度k
public void draw3D(Graphics g, int x1, int y1, int x2, int y2, int x3, int y3, int depth, int k) {
		if (depth > 1) {
//取震荡值
			double ranx1 = (x1 + x2) / k;
			double rany1 = (y1 + y2) / k;
			double ranx2 = (x2 + x3) / k;
			double rany2 = (y2 + y3) / k;
			double ranx3 = (x1 + x3) / k;
			double rany3 = (y1 + y3) / k;

			double Y1;
			double X2;
			double Y2;
			double X3;
			double Y3;
//中值震荡点
				X1 = (x1 + x2) / 2 + rand.nextInt((int) ranx1 * 2 + 1) - ranx1;
				Y1 = (y1 + y2) / 2 + rand.nextInt((int) rany1 * 2 + 1) - rany1;

				X2 = (x2 + x3) / 2 + rand.nextInt((int) ranx2 * 2 + 1) - ranx2;
				Y2 = (y2 + y3) / 2 + rand.nextInt((int) rany2 * 2 + 1) - rany2;

				X3 = (x1 + x3) / 2 + rand.nextInt((int) ranx3 * 2 + 1) - ranx3;
				Y3 = (y1 + y3) / 2 + rand.nextInt((int) rany3 * 2 + 1) - rany3;
//根据新的点迭代
			draw3D(g, (int) x1, (int) y1, (int) X1, (int) Y1, (int) X3, (int) Y3, depth - 1, k * 2);
			draw3D(g, (int) X1, (int) Y1, (int) x2, (int) y2, (int) X2, (int) Y2, depth - 1, k * 2);
			draw3D(g, (int) X1, (int) Y1, (int) X2, (int) Y2, (int) X3, (int) Y3, depth - 1, k * 2);
			draw3D(g, (int) X3, (int) Y3, (int) X2, (int) Y2, (int) x3, (int) y3, depth - 1, k * 2);

		} else {
			int[] px = { x1, x2, x3 };
			int[] py = { y1, y2, y3 };
			g.drawPolygon(px, py, 3);
		}
	}

我们看着这个代码会觉得没问题啊，逻辑很明确，但实际上这只完成了一半的工作，我们看看效果

出现了大量的空白，为什么？
我们把迭代次数调小一点看看

draw3D(g, x1, y1, x2, y2, x3, y3, /*9*/3, 8);

把9改为3
效果是这样的

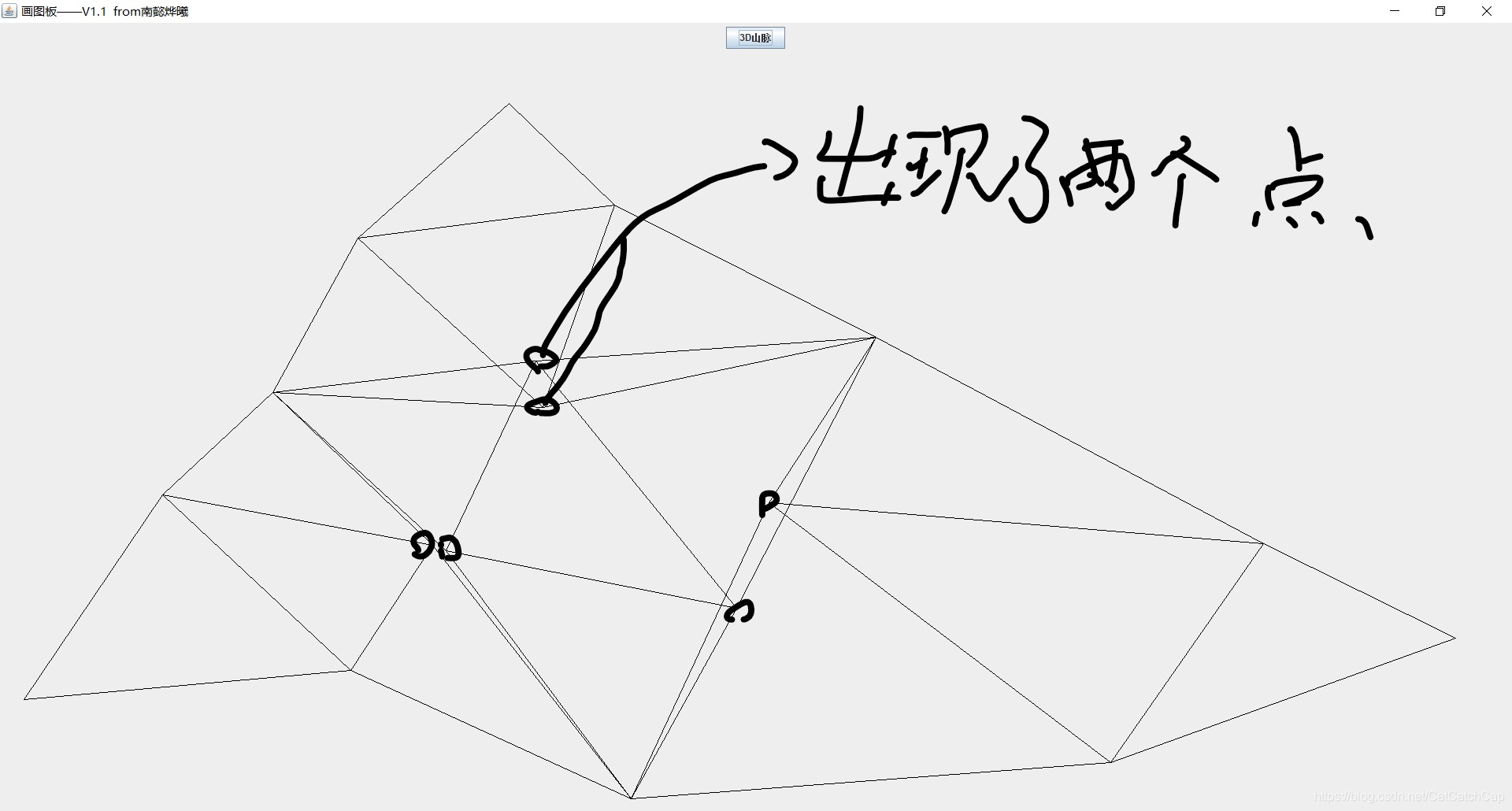
原来，在迭代取中值震荡点的时候取到了两次，就产生了两个震荡点，这就是问题所在。

问题解决

要解决这样的问题有很多种方法，主要思路就是将每次生成的边存起来（两个点确定一条边），如果在迭代的过程中出现了相同的点，那么就不再生成中值震荡点，选用最初产生的中值震荡点，所以我们想到建立一个存储点和中值震荡点的方法。我这里选用的是最基础的方法，创建一个类来储存。

此类如下

public class Points {
		Points(int x1, int x2, int y1, int y2, double X, double Y) {
			this.x1 = x1;
			this.x2 = x2;
			this.y1 = y1;
			this.y2 = y2;
			this.X = X;
			this.Y = Y;
		}

		int x1;
		int x2;
		int y1;
		int y2;
		double X;
		double Y;
	}
	Points[] po = new Points[5000000];//创建足够大的数组存储对象

接下来就好办了，
每次产生一个之前未出现的边时就将其存入数组对象中

Points p = new Points(x1, x2, y1, y2, X1, Y1);
				po[count ] = p;
				count++;

然后在每次迭代的时候判断此边是否出现过即可
完整代码如下

public class Points {
		Points(int x1, int x2, int y1, int y2, double X, double Y) {
			this.x1 = x1;
			this.x2 = x2;
			this.y1 = y1;
			this.y2 = y2;
			this.X = X;
			this.Y = Y;
		}

		int x1;
		int x2;
		int y1;
		int y2;
		double X;
		double Y;
	}

	Points[] po = new Points[5000000];
	Random rand = new Random();//创建随机数对象
	int count = 0;

	public void draw3D(Graphics g, int x1, int y1, int x2, int y2, int x3, int y3, int depth, int k) {
		if (depth > 1) {
			int u = 0, j = 0, o = 0;//这里必须要赋值，否则会报错说可能没有被赋予初始值，这个问题在c++里只是个warning。其实这里不赋值理论上也可，其没有值的时候也不会用到它们，细心的小伙伴可以看看是否是这样
			double ranx1 = (x1 + x2) / k;
			double rany1 = (y1 + y2) / k;
			double ranx2 = (x2 + x3) / k;
			double rany2 = (y2 + y3) / k;
			double ranx3 = (x1 + x3) / k;
			double rany3 = (y1 + y3) / k;
			boolean f1 = true;
			boolean f2 = true;
			boolean f3 = true;
			for (int i = 0; i < count; i++) {//边的确定，也就是两个点的确定一定要把x和y的坐标一起加上，我最开始认为只用判断横坐标即可，大家可以试试只判断横坐标出来的效果，我这里就不展示了
				if ((x1 == po[i].x1 && x2 == po[i].x2 && y1 == po[i].y1 && y2 == po[i].y2)
						|| (x1 == po[i].x2 && x2 == po[i].x1 && y1 == po[i].y2
								&& y2 == po[i].y1){
					f1 = false;
					u = i;
					break;
				}
			}
			for (int i = 0; i < count; i++) {
				if ((x2 == po[i].x1 && x3 == po[i].x2 && y2 == po[i].y1 && y3 == po[i].y2)
						|| (x2 == po[i].x2 && x3 == po[i].x1 && y2 == po[i].y2
								&& y3 == po[i].y1) {
					f2 = false;
					j = i;
					break;
				}
			}
			for (int i = 0; i < count; i++) {
				if ((x1 == po[i].x1 && x3 == po[i].x2 && y1 == po[i].y1 && y3 == po[i].y2)
						|| (x1 == po[i].x2 && x3 == po[i].x1 && y1 == po[i].y2
								&& y3 == po[i].y1) {
					f3 = false;
					o = i;
					break;
				}
			}
			double X1;
			double Y1;
			double X2;
			double Y2;
			double X3;
			double Y3;
			if (f1 == false) {
				X1 = po[u].X;
				Y1 = po[u].Y;
			} else {
				X1 = (x1 + x2) / 2 + rand.nextInt((int) ranx1 * 2 + 1) - ranx1;
				Y1 = (y1 + y2) / 2 + rand.nextInt((int) rany1 * 2 + 1) - rany1;
				Points p = new Points(x1, x2, y1, y2, X1, Y1);
				count++;
				po[count - 1] = p;
			}
			if (f2 == false) {
				X2 = po[j].X;
				Y2 = po[j].Y;
			} else {
				X2 = (x2 + x3) / 2 + rand.nextInt((int) ranx2 * 2 + 1) - ranx2;
				Y2 = (y2 + y3) / 2 + rand.nextInt((int) rany2 * 2 + 1) - rany2;
				Points p = new Points(x2, x3, y2, y3, X2, Y2);
				count++;
				po[count - 1] = p;
			}
			if (f3 == false) {
				X3 = po[o].X;
				Y3 = po[o].Y;
			} else {
				X3 = (x1 + x3) / 2 + rand.nextInt((int) ranx3 * 2 + 1) - ranx3;
				Y3 = (y1 + y3) / 2 + rand.nextInt((int) rany3 * 2 + 1) - rany3;
				Points p = new Points(x1, x3, y1, y3, X3, Y3);
				count++;
				po[count - 1] = p;
			}
			draw3D(g, (int) x1, (int) y1, (int) X1, (int) Y1, (int) X3, (int) Y3, depth - 1, k * 2);
			draw3D(g, (int) X1, (int) Y1, (int) x2, (int) y2, (int) X2, (int) Y2, depth - 1, k * 2);
			draw3D(g, (int) X1, (int) Y1, (int) X2, (int) Y2, (int) X3, (int) Y3, depth - 1, k * 2);
			draw3D(g, (int) X3, (int) Y3, (int) X2, (int) Y2, (int) x3, (int) y3, depth - 1, k * 2);

		} else {
			int[] px = { x1, x2, x3 };
			int[] py = { y1, y2, y3 };
			g.drawPolygon(px, py, 3);
		}
	}				

事实上，用数组来存点的效率是很低的，但是，说来惭愧，我能力有限，可能在之后掌握了map和list等用法过后会加以改进的吧，如果有感兴趣的朋友的话可以找我一起讨论讨论，我的QQ是 869083577.