蓝桥杯：递归 与 例题：斐波那契数列及优化与应用

 

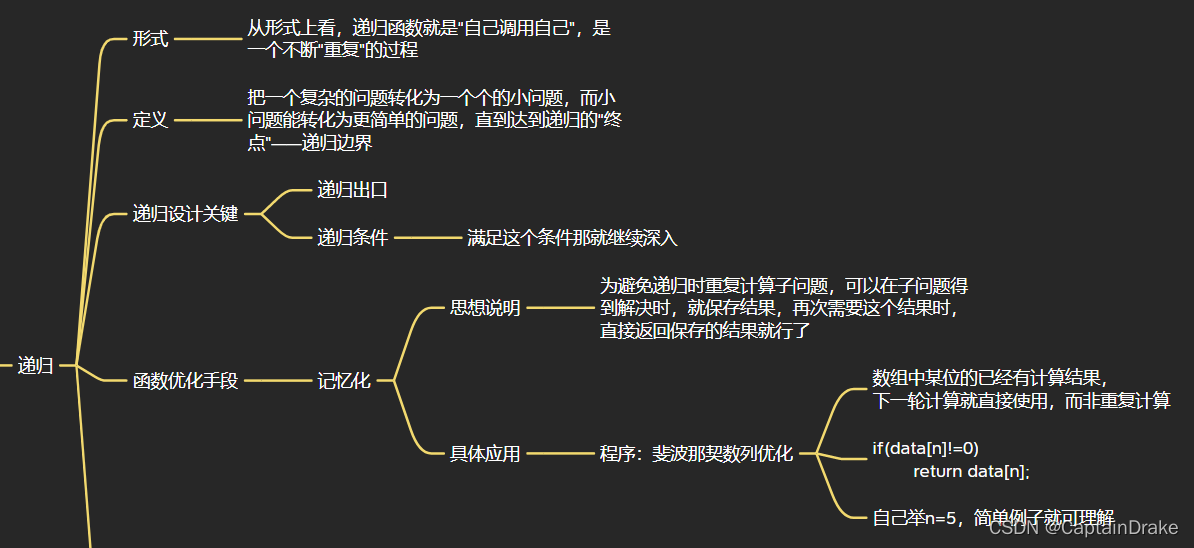
要想先搞DFS，那就先搞明白  递归

先上手一道简单递归题：斐波那契数列

#include <iostream>
using namespace std;
long int Leo(long int n);
int main()
{
    long n;
    cin>>n;//求Fibonacci数列的第n项
    cout<<Leo(n)<<endl;
    return 0;
}
long int Leo(long int n)
{
  if(n==0 || n==1)
    return n;
  else
    return Leo(n-1)+Leo(n-2);
}

结合图理解：

 

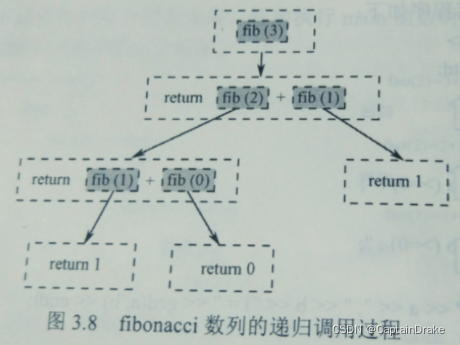
当数据大时，比如我们我们要求第10个斐波那契数时，

我们会遇到一个问题，比如程序在不断调用自己的过程中，它会不断地重复算

Leo（3），Leo（4），Leo（5）... 

那请问有没有一种方式能够直接调用以前计算过的值呢？

巧了，有的，那就是  记忆化

为避免递归时重复计算子问题，可以在子问题得到解决时，就保存结果，再次需要这个结果时，直接返回保存的结果就行了。这种存储已经解决的子问题结果的技术称为“记忆化（Memoization）