本文详细介绍了如何使用Python从头构建一个三层BP神经网络，包括参数初始化、正向传播、损失计算、反向传播等关键步骤，并结合交叉熵损失函数优化模型。适合初学者理解神经网络工作原理并实践基础模型。
BP神经网络（python）
神经网络基本结构
在用python搭建BP神经网络，其实可以直接调用sklearn。python是一种面向对象的语言，既然有现成的包可以直接调用，可以选择直接调用编译好的包。调用sklearn包更符合python编程的特性。
但是调用会对模型构成原理，造成模糊认识。本人认为从头开始实现一个神经网络是一个极具价值的代码编写过程，有助于加强对神经网络的认识，并且能够为之后实现更高级的神经网络打下基础。
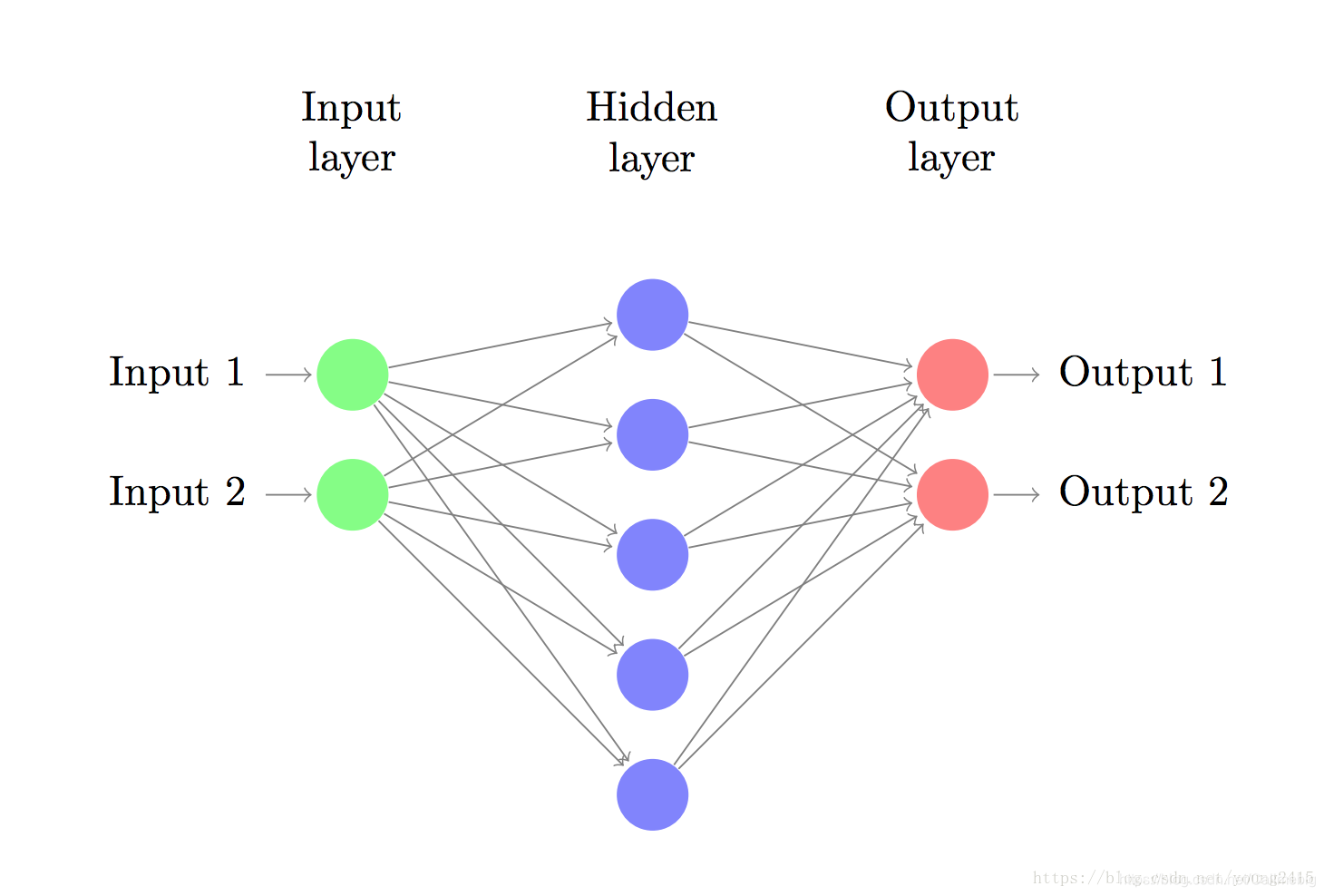
本文中，只是实现一个简单的三层神经网络（输入层、隐藏层、输出层）
BP神经网络的结构。
实现步骤
对BP神经网络代码的实现，需要明白神经网络具体包括哪几个步骤。
（1）初始化模型参数（w,b）；
（2）正向传播；
（3）计算损失值；
（4）反向传播；
（5）重复步骤（3）（4），得到最小loss值。
步骤细节
（1）初始化模型参数；
利用np.random.randn对模型参数进行初始化。
参数初始化的方法：
1.随机初始任意值；
2.基于正态分布设置模型参数；
3.模型参数随机范围进行限定，反正参数过大或者过小，影响传递。
下面展示一些 内联代码片。
// 参数的初始化
def initialize_parameters(n_x,n_h,n_y):
##n_x是样本特征数，n_h是隐藏层神经元个数，n_y是输出类别个数
np.random.seed(4)
w1=np.random.randn(n_x,n_h)##randn是生成0-1之间的数
b1=np.zeros(shape=(1,n_h))
w2=np.random.randn(n_h,n_y)
b2=np.zeros(shape=(1,n_y))
parameters={'w1':w1,'b1':b1,'w2':w2,'b2':b2}
return parameters
n_h∈特征数神经元个数
w1∈batch_size隐藏层神经元个数
b1∈batch_size隐藏层神经元个数
w2∈隐藏层神经元个数输出类别数
b2∈隐藏层神经元个数*输出类别数
（2）正向传播；
将训练样本与模型参数相乘，得到预测值。
y=f(wx+b)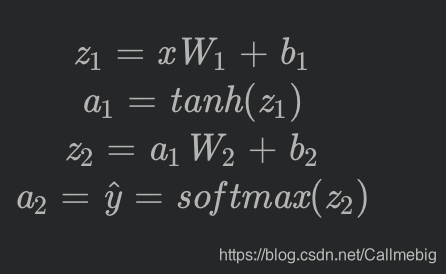
下面展示一些 内联代码片。
// 参数的初始化
def forward_propagation(X,parameters):
w1=parameters['w1']
b1=parameters['b1']
w2=parameters['w2']
b2=parameters['b2']
z1 = np.dot(X,w1) + b1##相加的话 只要列向量相同即可
a1=np.tanh(z1)
z2 = np.dot(a1,w2) + b2
a2=1/(1+np.exp(-z2))##使用sigmoid作为第二层的激活函数,使得输出在0-1之间
cache={'z1':z1,'a1':a1,'z2':z2,'a2':a2}
return a2,cache
（3）损失值；
计算预测值与真实值的差别。
创新点：各种损失函数–选择较好求导的损失函数
针对多分类的任务，通常使用交叉熵损失函数。
交叉熵损失函数的优点：
1.交叉熵能够衡量同一个随机变量中的两个不同概率分布的差异程度，在机器学习中表示为真实概率分布与预测概率分布之间的差异。交叉熵的值越小，模型预测效果越好。
2.交叉熵在分类问题中，常常与softmax一起使用。softmax将输出的结果进行处理，使其多个分类的预测值和为1，再通过交叉熵来计算损失。
3.利用交叉熵损失函数，最后一层权重的梯度不再与激活函数的导数相关，只跟输出值和真实值的差值成正比，此时收敛较快。（求导简单）
下面展示一些 内联代码片。
// 参数的初始化
def compute_cost(a2,Y,parameters):
m=Y.shape[0]
##采用交叉熵作为代价函数，交叉熵可以计算多分类任务的loss值
logprobs=np.multiply(np.log(a2),Y)+np.multiply((1-Y),np.log(1-a2))
cost=-np.sum(logprobs)/m
return cost
（4）反向传播
基于损失值，调整模型参数的值，进一步减少损失值。
提示：调整模型的参数可以改变最终的预测值，从而进一步改变损失值，但是具体增大还是减少参数的值，会减少最终的loss，是不确定的。因此，通过对loss函数求偏导，可以确定w的增大还是减少。因为求得导数的值，是损失函数减少最快的方向。但是参数变化的多少，由学习率决定。
大多数参数更新的方法都采用随机梯度下降（SGD），但是在SGD中学习率始终保持不变，因此衍生出其他学习率变化的算法，比如Adam。
下面展示一些 内联代码片。
def update_parameters(parameters,grads,learning_rate):
w1=parameters['w1']
b1=parameters['b1']
w2=parameters['w2']
b2=parameters['b2']
dw1=grads['dw1']
db1=grads['db1']
dw2=grads['dw2']
db2=grads['db2']
w1=w1-dw1*learning_rate
b1=b1-db1*learning_rate
w2=w2-dw2*learning_rate
b2=b2-db2*learning_rate
parameters={'w1':w1,'b1':b1,'w2':w2,'b2':b2}
return parameters
参数训练过程代码：
下面展示一些 内联代码片。
def nn_model(X,Y,n_h,n_input,n_output,num_iterations,learning_rate,print_cost=True):
np.random.seed(3)
n_x=n_input
n_y=n_output
parameters=initialize_parameters(n_x,n_h,n_y)
for i in range (0,num_iterations):
for i in range (X.shape[0]):
x_sample=X[i].reshape(1,n_input)
y_sample=train_y[i].reshape(1,n_output)
a2, cache=forward_propagation(x_sample,parameters)
cost=compute_cost(a2,y_sample,parameters)
grads=backward_propagation(parameters,cache,x_sample,y_sample)
parameters=update_parameters(parameters,grads,learning_rate)
if print_cost and i% 100==0:
print ('迭代第%i次，代价函数为:%f'%(i,cost))
return parameters
模型预测的过程：
下面展示一些 内联代码片。
def predict(parameters,x_test,y_test):
w1=parameters['w1']
b1=parameters['b1']
w2=parameters['w2']
b2=parameters['b2']
z1=np.dot(x_test,w1)+b1
a1=np.tanh(z1)
z2=np.dot(a1,w2)+b2
a2=1/(1+np.exp(-z2))
n_rows=y_test.shape[0]
n_cols=y_test.shape[1]
output=np.empty(shape=(n_rows,n_cols),dtype=int)
sorted_dist=np.argsort(a2)
for i in range(sorted_dist.shape[0]):
max_index=sorted_dist[i][3]
output[i][max_index]=1
for i in range(output.shape[0]):
for j in range(output.shape[1]):
if output[i][j]!=1:
output[i][j]=0
print('预测结果：')
print(output)
print('真实结果：')
print(y_test)
count=0
for i in range(output.shape[0]):
if output[i][0]==train_y[i][0] and output[i][1]==train_y[i][1] and output[i][2]==train_y[i][2]:
count=count+1
print ('预测准确的样本个数：%d'%count)
acc=count/int(y_test.shape[0])*100
print ('准确率：%.2f%%'%acc)
return acc
全部代码
下面展示一些 内联代码片。
#!/usr/bin/env python
# coding: utf-8
# In[411]:
import numpy as np
import pandas as pd
from sklearn.model_selection import train_test_split
from sklearn.metrics import classification_report
from sklearn.preprocessing import OneHotEncoder
# In[412]:
X=pd.read_csv('./data_1000.csv')
# In[413]:
label=X['label'].values
# In[414]:
label=label.reshape(label.shape[0],1)
# In[415]:
label=OneHotEncoder(sparse = False).fit_transform(label)
# In[416]:
label.shape
# In[417]:
feature=X.iloc[:,1:].values
# In[418]:
train_X,test_X,train_y,test_y = train_test_split(feature,label,test_size=0.4)
# In[419]:
from sklearn.preprocessing import StandardScaler
# In[420]:
scaler = StandardScaler() # 标准化转换
scaler.fit(train_X) # 训练标准化对象
train_X_standard= scaler.transform(train_X) # 转换数据集
# In[421]:
test_X_standard= scaler.transform(test_X)
# In[422]:
def initialize_parameters(n_x,n_h,n_y):
np.random.seed(4)
w1=np.random.randn(n_x,n_h)##randn是生成0-1之间的数
b1=np.zeros(shape=(1,n_h))
w2=np.random.randn(n_h,n_y)
b2=np.zeros(shape=(1,n_y))
parameters={'w1':w1,'b1':b1,'w2':w2,'b2':b2}
return parameters
# In[423]:
train_X_standard.shape
# In[424]:
def forward_propagation(X,parameters):
w1=parameters['w1']
b1=parameters['b1']
w2=parameters['w2']
b2=parameters['b2']
z1 = np.dot(X,w1) + b1##相加的话 只要列向量相同即可
a1=np.tanh(z1)
z2 = np.dot(a1,w2) + b2
a2=1/(1+np.exp(-z2))##使用sigmoid作为第二层的激活函数,使得输出在0-1之间
cache={'z1':z1,'a1':a1,'z2':z2,'a2':a2}
return a2,cache
# In[425]:
def compute_cost(a2,Y,parameters):
m=Y.shape[0]
##采用交叉熵作为代价函数，交叉熵可以计算多分类任务的loss值
logprobs=np.multiply(np.log(a2),Y)+np.multiply((1-Y),np.log(1-a2))
cost=-np.sum(logprobs)/m
return cost
def all_compute_cost(a2,Y,Y_all,parameters):
m=Y_all.shape[0]
logprobs=compute_cost(a2,Y,parameters)
cost=-np.sum(logprobs)/m
return cost
# In[426]:
parameters=initialize_parameters(n_x=23,n_h=40,n_y=4)
# In[427]:
a2,cache=forward_propagation(train_X_standard,parameters)
# In[428]:
cost=compute_cost(a2,train_y,parameters)
# In[ ]:
# In[429]:
def backward_propagation(parameters, cache, X ,Y):
m=Y.shape[0]
w2=parameters['w2']
a1=cache['a1']
a2=cache['a2']
dz2=a2-Y
dw2=(1/m)*np.dot(a1.T,dz2)
db2=(1/m)*np.sum(dz2,axis=1,keepdims=True)
dz1=np.multiply(np.dot(dz2,w2.T),1-np.power(a1,2))
dw1=(1/m)*np.dot(X.T,dz1)
db1=(1/m)*np.sum(dz1,axis=1,keepdims=True)
grads={'dw1':dw1,'db1':db1,'dw2':dw2,'db2':db2}
return grads
# In[430]:
grads=backward_propagation(parameters,cache,train_X_standard,train_y)
# In[431]:
def update_parameters(parameters,grads,learning_rate):
w1=parameters['w1']
b1=parameters['b1']
w2=parameters['w2']
b2=parameters['b2']
dw1=grads['dw1']
db1=grads['db1']
dw2=grads['dw2']
db2=grads['db2']
w1=w1-dw1*learning_rate
b1=b1-db1*learning_rate
w2=w2-dw2*learning_rate
b2=b2-db2*learning_rate
parameters={'w1':w1,'b1':b1,'w2':w2,'b2':b2}
return parameters
# In[432]:
train_X_standard.shape
# In[433]:
x_sample=train_X_standard[1].reshape(23,1)
x_sample.shape
# In[434]:
def nn_model(X,Y,n_h,n_input,n_output,num_iterations,learning_rate,print_cost=True):
np.random.seed(3)
n_x=n_input
n_y=n_output
parameters=initialize_parameters(n_x,n_h,n_y)
for i in range (0,num_iterations):
for i in range (X.shape[0]):
x_sample=X[i].reshape(1,n_input)
y_sample=train_y[i].reshape(1,n_output)
a2, cache=forward_propagation(x_sample,parameters)
cost=compute_cost(a2,y_sample,parameters)
grads=backward_propagation(parameters,cache,x_sample,y_sample)
parameters=update_parameters(parameters,grads,learning_rate)
if print_cost and i% 100==0:
print ('迭代第%i次，代价函数为:%f'%(i,cost))
return parameters
# In[435]:
parameters=nn_model(train_X_standard,train_y,n_h=40,n_input=train_X_standard.shape[1],n_output=4,num_iterations=1000,learning_rate=0.01,print_cost=True)
# In[436]:
def predict(parameters,x_test,y_test):
w1=parameters['w1']
b1=parameters['b1']
w2=parameters['w2']
b2=parameters['b2']
z1=np.dot(x_test,w1)+b1
a1=np.tanh(z1)
z2=np.dot(a1,w2)+b2
a2=1/(1+np.exp(-z2))
n_rows=y_test.shape[0]
n_cols=y_test.shape[1]
output=np.empty(shape=(n_rows,n_cols),dtype=int)
sorted_dist=np.argsort(a2)
for i in range(sorted_dist.shape[0]):
max_index=sorted_dist[i][3]
output[i][max_index]=1
for i in range(output.shape[0]):
for j in range(output.shape[1]):
if output[i][j]!=1:
output[i][j]=0
print('预测结果：')
print(output)
print('真实结果：')
print(y_test)
count=0
for i in range(output.shape[0]):
if output[i][0]==train_y[i][0] and output[i][1]==train_y[i][1] and output[i][2]==train_y[i][2]:
count=count+1
print ('预测准确的样本个数：%d'%count)
acc=count/int(y_test.shape[0])*100
print ('准确率：%.2f%%'%acc)
return acc
# In[437]:
acc=predict(parameters,train_X_standard,train_y)
# In[438]:
# In[ ]:
扫一扫
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
