Codeforces Round #670 (Div. 2) 题解_given a set of integers (it can contain equal elem-优快云博客

菜鸡学习笔记

A. Subset Mex

题干:

Given a set of integers (it can contain equal elements).

You have to split it into two subsets A and B (both of them can contain equal elements or be empty). You have to maximize the value of mex(A)+mex(B).

Here mex of a set denotes the smallest non-negative integer that doesn’t exist in the set. For example:

mex({1,4,0,2,2,1}) = 3
mex({3,3,2,1,3,0,0}) = 4
mex(∅) = 0(mex for empty set)

The set is splitted into two subsets A and B if for any integer number x the number of occurrences of x into this set is equal to the sum of the number of occurrences of x into A and the number of occurrences of x into B.

限制

time limit per test 1 s

memory limit per test 512 M

Input

The input consists of multiple test cases. The first line contains an integer t (1≤t≤100) — the number of test cases. The description of the test cases follows.

The first line of each test case contains an integer n (1≤n≤100) — the size of the set.

The second line of each test case contains n integers $a_1, a_2.... a_n$ (0≤ $a_i$ ≤100) — the numbers in the set.

Output

For each test case, print the maximum value of mex(A)+mex(B).

题目大意

签到题，直接上代码

#include <bits/stdc++.h>
using namespace std;
int num[110] = { 0 };
int n;
int main()
{
    int t, temp;
    cin >> t; 
    while (t--) {
        scanf("%d", &n);
        memset(num, 0, sizeof(num));
        int maxx = -1;
        for (int i = 0; i < n; i++) {
            scanf("%d", &temp);
            num[temp]++;
            maxx = max(maxx, temp);
        }
        int ans = 0;
        int flag1 = 0;
        for (int i = 0; i <= maxx + 1; i++) {
            if (num[i] < 2 && flag1 == 0) {
                ans += i;
                flag1 = 1;
            }
            if (flag1 == 1&&num[i]==0) {
                ans += i;
                break;
            }
        }
        printf("%d\n", ans);
    }
    return 0;
}

B. Maximum Product

题干:

You are given an array of integers $a_1, a_2.... a_n$ . Find the maximum possible value of $a_i a_j a_k a_l a_t$ among all five indices (i,j,k,l,t)(i<j<k<l<t).

限制

time limit per test 2 s

memory limit per test 512 M

Input

The input consists of multiple test cases. The first line contains an integer t (1 ≤ t ≤ 2⋅10⁴) — the number of test cases. The description of the test cases follows.

The first line of each test case contains a single integer n (5≤n≤10⁵) — the size of the array.

The second line of each test case contains n integers $a_1, a_2.... a_n$ (−3×10³ ≤ ai ≤ 3×10³) — given array.

It’s guaranteed that the sum of n over all test cases does not exceed 2⋅10⁵.

Output

For each test case, print one integer — the answer to the problem.

题目大意

给 t 个数组，每个数组选择5个数，求这5个数的乘积最大

题解

5个数，可以分成 x 个负数，5 - x 个非负数，可以枚举 6 种情况(x = 0…x = 1…x = 2等)

(我是这么做的,如果有更好的方法欢迎批评指正)

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int MAX = 1e5 + 10;
const ll MIN = -1e18;
ll num[MAX] = { 0 };
int n;
int main()
{
    int  t;
    cin >> t;
    while (t--) {
        scanf("%d", &n);
        int ne = 0, nne = 0;//ne为负数，nne为非负数
        for (int i = 0; i < n; i++) {
            scanf("%lld", &num[i]);
            if (num[i] >= 0) nne++;
            else ne++;
        }
        sort(num, num + n);
        int zz = n - 1;
        for (int i = 0; i < n; i++) {
            if (num[i] >= 0) {
                zz = i;
                break;
            }
        }
        ll ans = MIN;
        ll temp = 1;
        if (nne >= 5) {
            int cnt = 0;
            for (int i = n - 1; i >= 0; i--) {
                temp *= num[i];
                cnt++;
                if (cnt >= 5) break;
            }
            ans = max(ans, temp);
        }
        if (nne >= 4 && ne >= 1) {
            int cnt = 0;
            temp = 1;
            for (int i = n - 1; i >= 0; i--) {
                temp *= num[i];
                cnt++;
                if (cnt >= 4) break;
            }
            temp *= num[zz - 1];
            ans = max(ans, temp);
        }
        if (nne >= 3 && ne >= 2) {
            int cnt = 0;
            temp = 1;
            for (int i = n - 1; i >= 0; i--) {
                temp *= num[i];
                cnt++;
                if (cnt >= 3) break;
            }
            temp *= num[0]*num[1];
            ans = max(ans, temp);
        }
        if (nne >= 2 && ne >= 3) {
            int cnt = 0;
            temp = 1;
            for (int i = zz + 1; i >= 0; i--) {
                temp *= num[i];
                cnt++;
                if (cnt >= 5) break;
            }
            ans = max(ans, temp);
        }
        if (nne >= 1 && ne >= 4) {
            int cnt = 0;
            temp = 1;
            for (int i = 0; i < n; i++) {
                temp *= num[i];
                cnt++;
                if (cnt >= 4) break;
            }
            temp *= num[n-1];
            ans = max(ans, temp);
        }
        if (ne >= 5) {
            int cnt = 0;
            temp = 1;
            for (int i = zz; i >= 0; i--) {
                temp *= num[i];
                cnt++;
                if (cnt >= 5) break;
            }
            ans = max(ans, temp);
        }
        printf("%lld\n", ans);
    }
    return 0;
}

C. Link Cut Centroids

题干:

Fishing Prince loves trees, and he especially loves trees with only one centroid. The tree is a connected graph without cycles.

A vertex is a centroid of a tree only when you cut this vertex (remove it and remove all edges from this vertex), the size of the largest connected component of the remaining graph is the smallest possible.

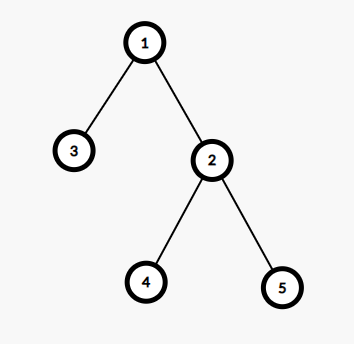
For example, the centroid of the following tree is 2, because when you cut it, the size of the largest connected component of the remaining graph is 2 and it can’t be smaller.

However, in some trees, there might be more than one centroid, for example:

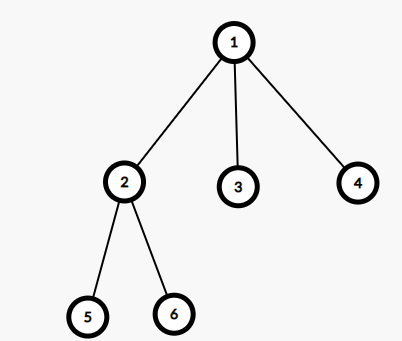
Both vertex 1 and vertex 2 are centroids because the size of the largest connected component is 33 after cutting each of them.

Now Fishing Prince has a tree. He should cut one edge of the tree (it means to remove the edge). After that, he should add one edge. The resulting graph after these two operations should be a tree. He can add the edge that he cut.

He wants the centroid of the resulting tree to be unique. Help him and find any possible way to make the operations. It can be proved, that at least one such way always exists.

限制

time limit per test 1 s

memory limit per test 512 M

Input

The input consists of multiple test cases. The first line contains an integer t (1≤t≤10⁴) — the number of test cases. The description of the test cases follows.

The first line of each test case contains an integer n (3 ≤n ≤10⁵) — the number of vertices.

Each of the next $n - 1$ lines contains two integers $x, y$ ( $1 \leq x, y \leq n$ ). It means, that there exists an edge connecting vertices $x$ and $y$ .

It’s guaranteed that the given graph is a tree.

It’s guaranteed that the sum of $n$ for all test cases does not exceed $10^5$ .

Output

For each test case, print one integer — the answer to the problem.

题目大意

给一棵树,删一条边，并增加一条边,使得清除一个节点 (删除结点以及与这个节点所连接的边) 后,能够使得剩余最大连通分量最小，并且保证这种可清除节点唯一 , 这里的最大连通分量就是清除节点后剩余的所有树，描述的大小指每颗树的节点个数。

题解(个人理解以及参考网上大神)

首先要解决的问题是，如何才能使剩余最大连通分量最小，这里可以看到是只清除一个节点，可以设这个节点为 $x$ ,很容易可以理解，如果清除 $x$ 节点后只生成两棵树，那么此时会产生最大的连通分量，可以假设生成的左树 $T_l$ 右树 $T_r$ ,左树有节点数为 $S_l$ ，右树有节点个数为 $S_r$ ,那么有1 + $S_l$ + $S_r$ = n ,题目要求 $min \{S_l,S_r\}$ ,即 $min \{S_l,n - S_l - 1\}$
根据单调性可知，当 $S_l=n-S_l-1$ → $Sl=n−12S_l=\frac{n-1}{2}$ ，此时可以保证最大连通分量最小
所以上面这一通证明是干嘛的呢，就是证明要求的这个清除节点 $x$ 是树的中间节点(平分权重的点)
那就可以通过一顿 $D F S$ ，得到要求的中间点
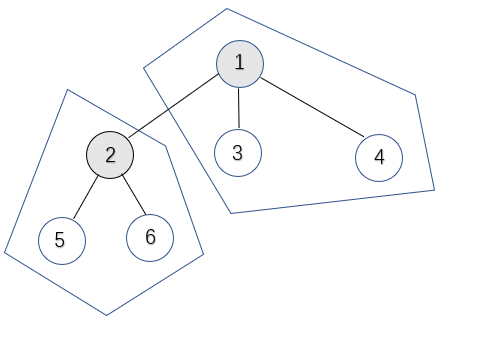
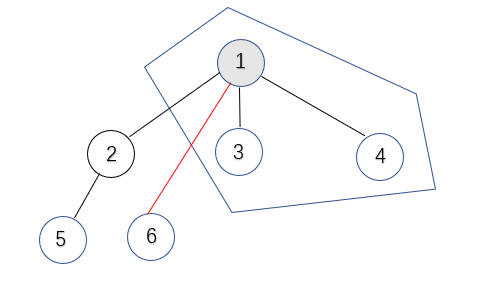
注意 : 上面假定的平分只生成两棵树，事实上，左树是多个子树的集合，右树同样也是，只不过左树总节点数目恰好与右树总结点数目相同

但是可以找到这个假定存在的问题，如果数的点为偶数，平分的操作就会产生两个符合的点 ,那么就不符合题目要求的唯一，解决方案就是破坏其种一个点的结构，使得符合的点唯一。事实上，可以很容易证明出,这两个符合的点是相连的，并且去掉此边，生成的两棵树的大小均为 $n2\frac{n}{2}$ ，不妨设破坏遍历到的第1颗树的结构,解决方案就是将此树随意的叶节点孤立 (即去掉与这个叶节点所连接的边),并且将此叶节点直接连接给另一个符合平分条件的点。如图:

代码完成以上操作

#include <bits/stdc++.h>
using namespace std;
const int MAX = 1e5 + 10;
vector<int> g[MAX];
vector<int> ans;
int n;
int le1, le2;
int dfs(int x, int fa) {
    int re = 1, judge = 1;
    for (int i = 0; i < g[x].size(); i++) {
        if (g[x][i] == fa) continue;
        int temp = dfs(g[x][i],x);
        if (temp > n / 2) judge = 0;
        re += temp;
    }
    if (re < n - n / 2) judge = 0;
    if (judge) ans.push_back(x);
    return re;
}
void dfs2(int x, int fa) {
    int judge = 1;
    for (int i = 0; i < g[x].size(); i++) {
        if (g[x][i] == fa) continue;
        dfs2(g[x][i], x);
        judge = 0;
    }
    if (judge) {
        le1 = x;
        le2 = fa;
    }
}
int main()
{
    int t;
    cin >> t;
    int a, b;
    while (t--) {
        scanf("%d", &n);
        int l1, l2;
        ans.clear();
        for (int i = 1; i <= n; i++) {
            g[i].clear();
        }
        for (int i = 0; i < n - 1; i++) {
            scanf("%d %d", &a, &b);
            g[a].push_back(b);
            g[b].push_back(a);
            l1 = a;
            l2 = b;
        }
        dfs(1, 0);
        if (ans.size() == 1) {
            printf("%d %d\n%d %d\n", l1, l2, l1, l2);
        }
        else {
            dfs2(ans[0], ans[1]);
            printf("%d %d\n%d %d\n", le1, le2, le1, ans[1]);
        }
    }
    return 0;
}

D. Three Sequences

题干:

You are given a sequence of $n$ integers $a_1, a_2.... a_n$ .

You have to construct two sequences of integers $b$ and $c$ with length $n$ that satisfy:

for every ii ( $1 \leq i \leq n$ ) $b_i+c_i=a_i$
$b$ is non-decreasing, which means that for every $1 < i \leq n$ , $b_i≥b_{i-1}$ must hold
cc is non-increasing, which means that for every $1 < i \leq n$ , $c_i≤c_{i-1}$ must hold

You have to minimize $max(b_i,c_i)$ . In other words, you have to minimize the maximum number in sequences $b$ and $c$ .

Also there will be $q$ changes, the $i$ -th change is described by three integers $l, r, x$ . You should add $x$ to $a_l, a_{l+1}.... a_r$ .

You have to find the minimum possible value of $max(b_i,c_i)$ for the initial sequence and for sequence after each change.

限制

time limit per test 2 s

memory limit per test 512 M

Input

The first line contains an integer $n$ ( $1≤n≤10^5$ ).

The second line contains $n$ integers $a_1,a_2,...,a_n$ ( $1 \leq i \leq n$ , $10^9≤i≤10^9$ ).

The third line contains an integer $q$ ( $1≤q≤10^5$ ).

Each of the next $q$ lines contains three integers $l, r, x$ ( $1 \leq l \leq r \leq n$ , $10^9≤x≤10^9$ ) , desribing the next change.

Output

Print $q + 1$ lines.

On the $i$ -th ( $1 \leq i \leq q + 1$ ) line, print the answer to the problem for the sequence after $i - 1$ changes.

题目大意

已知一个序列 $a$ ,让我们自己拟合一个单调递增的序列 $b$ 和单调递减的序列 $c$ ,并且对于每个 $a_i$ 有 $b_i + c_i = a_i$ ,求 $max(b_i,c_i)$ ,其实就是求 $max(b_n,c_1)$ 的最小值

题解

个人认为这道题比C还要简单一些，是一道比较简单的差分问题，对于 $a_{i+1}-a_i = d$ ,可以很容易得知道，若 $d > 0$ ,就将 $d$ 加到 $b$ 的下一个点上(否则 $b_n$ 的值要更大),若 $d < 0$ ,就将 $d$ 加到 $c$ 上， $d = 0$ 就不变。假设 $b, c$ 分别的初始值为 $x, y$ , $\sum_{i=1}^nd_i (d_i>0)$ ,所求的值即为 $m a x (x + z, y)$ 的最小值 , 而且有 $x + y = a [1]$ , 根据单调性也有:当 $x + z = y$ 时有最小值，经过代换可得: $x=a[1]−z2x=\frac{{a[1]-z}}{2}$ , 最终结果即为 $m a x (x + z, a [1] - x)$ ,代码完成即可.

#include <bits/stdc++.h>
typedef long long ll;
using namespace std;
const int MAX = 1e5 + 10;
int n, q, l, r;
ll a[MAX] = { 0 }, d[MAX] = { 0 };
ll z = 0, val;
int main()
{
    cin >> n;
    for (int i = 1; i <= n; i++) {
        scanf("%lld", &a[i]);
        d[i] = a[i] - a[i - 1];
    }
    for (int i = 2; i <= n; i++) {
        if (d[i] > 0) z += d[i];
    }
    ll x = (a[1] - z) / 2;
    printf("%lld\n", max(x + z, a[1] - x));
    cin >> q;
    while (q--) {
        scanf("%d %d %lld", &l, &r, &val);
        if (l == 1) {
            d[1] += val;
        }
        else {
            if (val > 0 ) {
                if(d[l] + val > 0)  z += min(d[l] + val, val);
            }
            else {
                if (d[l] > 0) z -= min(-val, d[l]);
            }
            d[l] += val;
        }
        if (r + 1 <= n) {
            if (val > 0) {
                if (d[r + 1] > 0)  z -= min(d[r + 1], val);
            }
            else {
                if (d[r + 1] - val > 0) z += min(-val, d[r + 1] - val);
            }
            d[r + 1] -= val;
        }
        x = (d[1] - z) / 2;
        printf("%lld\n", max(x + z, d[1] - x));
    }
    return 0;
}