数据结构——图

  

目录

1 图的定义

1.1 无向图和有向图

1.2 简单图和多重图

1.3 顶点的度、入度、出度

1.4 顶点-顶点的关系描述 

1.5 连通图与强连通图 

1.6 子图 

1.7 连通分量和强连通分量

1.8 生成树和生成森林

1.9 边的权、带权图/网

1.10 几种特殊形态的图

2 邻接矩阵

2.1 存储形式

2.2 构建邻接矩阵的基本步骤：

2.2 邻接矩阵的优缺点

2.3 邻接矩阵法的性质

3 邻接表

3.1 存储形式

3.2 构建邻接表的基本步骤

3.3 邻接表的优缺点

3.4 对比邻接矩阵与邻接表

4 十字链表和邻接多重表

5 图的基本操作 

6 图的遍历

6.1 深度优先遍历(DFS)

6.1.1 DFS定义

6.1.2 递归实现DFS

6.1.3 非递归实现DFS 

6.1.4 结论

6.2 广度优先遍历(BFS)

7 最小生成树 

7.1 最小生成树概念

7.2 Prim算法（普⾥姆）求最小生成树

7.3 Kruskal 算法（克鲁斯卡尔）求最小生成树

8 最短路径 

8.1 BFS算法

8.2 Dijskra算法

8.3 Floyd算法

---

1 图的定义

图(Graph):由两个集合边集和点集【V(vertex)和E(edge)】组成，记作G = (V,E)。其中V是各顶点（结点)，V中的任意两个顶点配对后作为边集合E的元素。

1.1 无向图和有向图

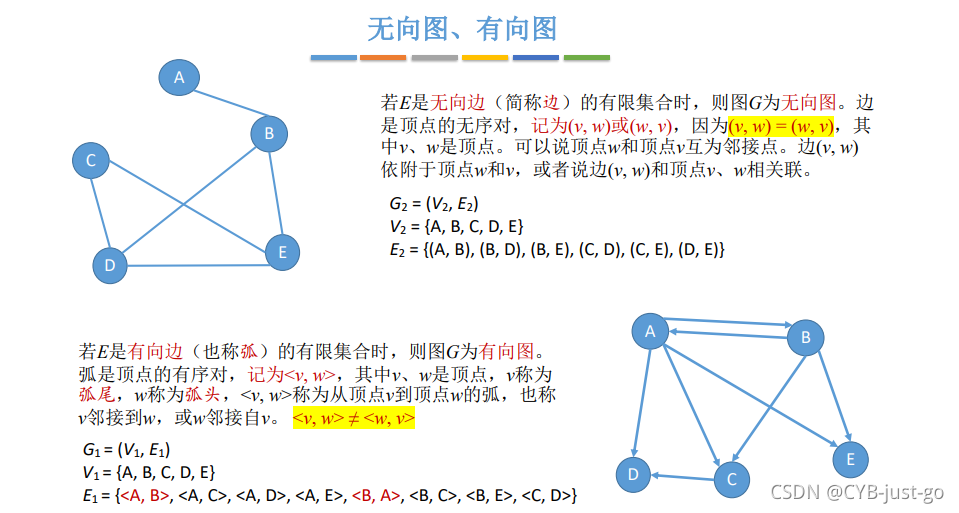
在有向图中，E中的元素形式为<x,y>，表示从顶点x到顶点y的一条有向边，有向边也称作弧，x为弧尾，y为弧头；

在无向图中，E中的元素形式为(x,y)，仅表示连接顶点x和顶点y的一条边，效果同(y,x)。

1.2 简单图和多