Python 实验四 循环结构

一、实验目的

（1）掌握循环的概念，能够用循环结构来解决算法问题

（2）熟练掌握实现遍历循环操作的for语句

（3）熟练掌握实现无线循环操作的while语句

（4）掌握用来辅助控制循环执行的break和continue语句

二、实验环境

联网计算机一台/每人，内装Windows 7以上操作系统和安装Python 3.7集成开发环境IDLE。

三、实验内容

Sy4-1

有一个分数序列2/1,3/2,5/3,8/5,13/8,21/13,编程计算这个序列前20项之和。

Sy4-2

设计一个“过七游戏”，这个游戏由5人以上参与，任意一人从1开始数数，当遇到7或者7的倍数或者含有数字7时，必须以敲桌子代替，报出的人输。

Sy4-3

如果将20元换成零钱，要求只能换成1元、5元、10元的纸币，共有多少种方法。

Sy4-4

编程计算自然对数e的近似值，要求其误差小于0.00001，公式为e=1+1/1!+1/2!+1/3!+…+1/n!+…。

Sy4-5

编程找出1000以内的所有完数，一个数如果恰好等于它的因子之和，这个数称为完数，例如6=1+2+3。

拓展

1.编写程序，输入任意一个整数，判断该整数是否为素数，并输出判断结果。

2.编写程序，将一个正整数分解为质因数并输出，例如90=2*3*3*5

四、实验步骤与结果

1. 新建文件夹并命名为学号-姓名-实验四。

2. 安装 Python 解释器Python 3.7 集成开发环境IDLE，并进入IDLE。

3. 依次输入自己编好的程序实验内容1-7的源程序，分别命名为sy4_1.py - sy4_7.py 并保存至已建好的文件夹中。

4. 检查已输入的程序是否有错（包括输入时输错的和编程中的错误），如发现有错，及时改正。

5. 运行程序并分析运行结果是否合理。在运行时要注意当输入不同的数据时所得结果是否正确，应测试两组以上数据，分别检查在不同情况下结果是否正确。

列出1-7题源程序清单并记录上机运行结果。

Sy4-1

有一个分数序列2/1,3/2,5/3,8/5,13/8,21/13,编程计算这个序列前20项之和。

a,b,s,t = 1,1,0,0
for n in range(1,21):
    t=a
    a=a+b
    b=t
    s+=a/b
print("2/1+3/2+5/3+8/5+13/8+...=%.2f" %s)

Sy4-2

设计一个“过七游戏”，这个游戏由5人以上参与，任意一人从1开始数数，当遇到7或者7的倍数或者含有数字7时，必须以敲桌子代替，报出的人输。

n = 0
while n <= 99:
    n = n + 1
    if (n % 7 == 0) or (n % 10 == 7) or (n // 10 == 7):
        print("敲桌子")
    else:
        print(n)

//运行结果
1
2
3
4
5
6
敲桌子
8
9
10
11
12
13
敲桌子
15
16
敲桌子
18
19
20
敲桌子
22
23
24
25
26
敲桌子
敲桌子
29
30
31
32
33
34
敲桌子
36
敲桌子
38
39
40
41
敲桌子
43
44
45
46
敲桌子
48
敲桌子
50
51
52
53
54
55
敲桌子
敲桌子
58
59
60
61
62
敲桌子
64
65
66
敲桌子
68
69
敲桌子
敲桌子
敲桌子
敲桌子
敲桌子
敲桌子
敲桌子
敲桌子
敲桌子
敲桌子
80
81
82
83
敲桌子
85
86
敲桌子
88
89
90
敲桌子
92
93
94
95
96
敲桌子
敲桌子
99
100

Sy4-3

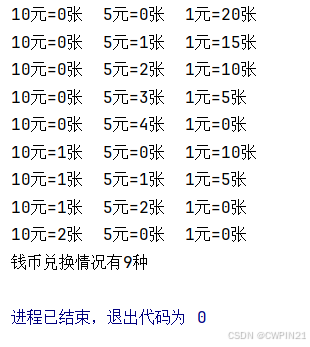
如果将20元换成零钱，要求只能换成1元、5元、10元的纸币，共有多少种方法。

n=0
for x in range(3):              # 10元面值个数从0到2
    for y in range(5):          # 5元面值个数从0到4
        for z in range(21):     # 1元面值个数从0到20
            if x*10+y*5+z==20:
                print('10元=%d张  5元=%d张  1元=%d张  '%(x, y, z))
                n+=1
print('钱币兑换情况有%d种'%n)

Sy4-4

编程计算自然对数e的近似值，要求其误差小于0.00001，公式为e=1+1/1!+1/2!+1/3!+…+1/n!+…。

from math import e 
print("math库里数学常数e的值是：",e) 
x,i,n,t=0,0,1,1 
while t>=0.00001: 
    x=x+t 
    i=i+1 
    n=n*i 
    t=1/n 
print("利用级数公式所求的e近似值是：",x) 

Sy4-5

编程找出1000以内的所有完数，一个数如果恰好等于它的因子之和，这个数称为完数，例如6=1+2+3。

for x in range(1,1000): 
    sum = 0
    for i in range(1,x): 
       if x % i == 0: 
         sum = sum+ i 
    if sum == x: 
         print("%d是完数"%x) 

拓展

1.编写程序，输入任意一个整数，判断该整数是否为素数，并输出判断结果。

num=int(input("输入一个整数："))
i = 2
while(i < num):    #此循环判断某一个num是否有因子
    if (num % i==0):
        break
    i=i+ 1
if (i==num) :
    print(num,"是素数")
else:
    print(num,"有因子",i,",不是素数")

2.编写程序，将一个正整数分解为质因数并输出，例如90=2*3*3*5

n=int(input("输入任意一个正整数："))
print("%d="%n,end="")
for k in range(2,n+1):
    while n!=k:
        if n%k==0:
            n=n/k
            print("%d * "%k,end="")
        else:
            break
print("%d"%n)

五、总结

1. 实验过程中的问题及解决方法：

问题 1：无限循环导致程序崩溃 在编写一个`while`循环时，由于没有正确设置循环结束的条件，导致程序陷入了无限循环，最终崩溃。

解决方法：仔细检查循环条件，确保在合适的时候能够退出循环。通过添加一个计数器或者根据特定的条件来控制循环的结束。

问题 2：循环逻辑错误 在一个`for`循环中，期望对列表中的每个元素进行特定操作，但由于循环逻辑错误，导致部分元素被跳过或重复处理。

解决方法：重新审视循环的逻辑，使用正确的索引或遍历方式来确保每个元素都能被准确处理。通过打印中间结果来调试和检查循环的执行过程。

2. 实验收获

        通过本次关于 Python 循环结构的实验，我获得了以下宝贵的经验和知识： 1. 深入理解了`for`循环和`while`循环的工作原理及适用场景。能够根据不同的需求选择合适的循环结构来提高程序的效率和可读性。 2. 掌握了如何设置合理的循环条件，避免出现无限循环或逻辑错误。这对于编写稳定可靠的程序至关重要。 3. 学会了在循环中使用`break`和`continue`语句来控制程序的流程，增强了对程序执行路径的掌控能力。 4. 通过解决实验中遇到的问题，提高了自己的调试和错误处理能力。能够更加熟练地运用打印中间结果、查看变量值等方法来定位和解决问题。 5. 认识到了在编写循环代码时，清晰的逻辑和良好的代码结构的重要性。这有助于提高代码的可维护性和可扩展性。