三维世界离不开的四元数？心领神会“复杂的简单”-优快云博客

作者 | 绯红之刃编辑 | 3D视觉之心

原文链接：https://zhuanlan.zhihu.com/p/636543643

点击下方卡片，关注“自动驾驶之心”公众号

本文只做学术分享，如有侵权，联系删文

本文讲一个数学上比较有趣的东西：四元数。我们用复数（两个数字）可以表示二维上的旋转，那么是不是用三个数字（三元数）可以表示三维空间中的旋转呢？数学家告诉我们不是的，要表示三维空间中的旋转，我们得用四元数。四元数这个东西有个特点，就是它用起来很简单，但是推导、证明过程非常的复杂，而且理解起来也非常的抽象。有没有什么办法，让我们用比较简单的方式理解这个东西呢？其实是有的。本文提供一种尽可能非常简单的视角，全文不会涉及复杂的公式、推导，基本上应该让你可以轻松接受四元数这个东西。而且，本文会顺带讲讲为什么要造出四元数这么个东西，它是怎么扩展出来的，它还能怎么扩展。

首先说说我为什么认为四元数这个东西，虽然推导过程非常繁琐、构造过程非常抽象，但是却可以通过简单的方式来理解呢？因为数学上有的东西它有这样的特点，就是你看起来觉得它不复杂，理解起来不复杂，而且用起来也不复杂，但是推导过程却很繁琐，我心目中几个比较典型的例子是，微积分里的斯托克斯公式（也叫斯托克斯环流公式）、线性代数里的Jordan标准型（也叫约旦标准型、若尔当标准型）、概率论里的中心极限定理、代数里的虚数（虚数在历史上其实是来源于一元三次方程求根公式，而不是一元二次方程，历史上人们理解它是花了比较大的功夫的）。就是说数学上是有不少那种理解起来简单，用起来也简单，但是证明起来很繁琐的东西的。四元数我觉得其实也可以作为其中一元。

数学中的“复杂的简单”

说到这里，稍微扯点废话吧。数学里面有的东西推导起来复杂，但是用起来、理解起来，都比较简单。我稍微讲讲刚才举的那几个例子。这里只是为了让你理解一个推导起来复杂的东西怎么理解起来简单的。如果你不想看这一部分，可以直接翻到我目录的下一节看。

斯托克斯公式：

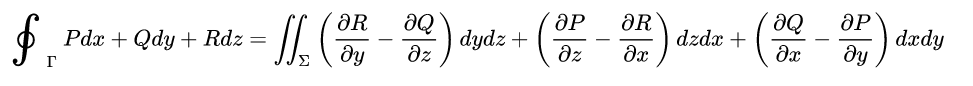
这个东西证明起来不难，但是有点繁琐。但是理解起来却很简单，你只要把它跟格林公式类比一下就好了。格林公式：

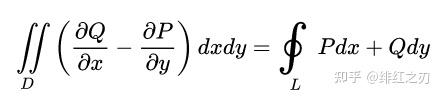
你把一个曲面投影到XOY平面上，它就是格林公式，然后再分别投影到YOZ，ZOX平面上，加起来，就是斯托克斯公式。这么说的话其实不太合理，因为你把它直接加起来的话发现系数差个2倍。我换个说法，斯托克斯公式的那个环路，你把它投射到XOY平面上就是格林公式，类似地，你投射到YOZ平面，也是格林公式，投射到ZOX平面上，也是格林公式。当然这么说不太严谨，但是对你理解来说足够了。

但是你要证明这个东西的话有点繁琐，你要把z写成x和y的函数，然后求导，合并什么的。

Jordan标准型：

这个东西就是那种，理解上很直观，但是也是那种推导上比较繁琐的东西。这是个啥呢？就是我们线性代数上讲，我们希望一个nxn的方阵有n个特征向量，这样它就可以对角化（方阵可对角化的充要条件是它有n个特征向量）。什么是可对角化呢？就是可以化成这么个东西：

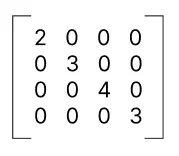
但是有的矩阵不可对角化，这样的矩阵是怎么回事呢？这样的矩阵首先有个特征，就是它有重复的特征值（特征方程有重根），比如说它有2个特征值都是3。但是它的特征向量的数量比特征值的重数少，比如特征值3对应的特征向量只有1个，那么它就少了一个特征向量。这样它就不可对角化。那我们能不能化成那种类似对角阵的东西呢？Jordan告诉我们，可以，就是化成下面这种东西：

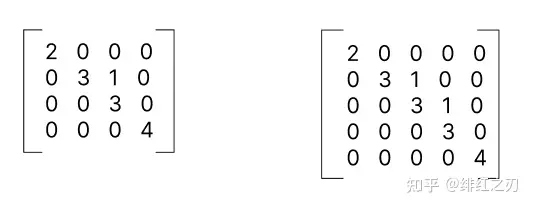
这个东西理解起来非常简单。无非就是没法对角化的时候，把几个3上面那个位置上的0变成1就行了，这样是让它最像对角化的形式。但是我不知道是怎么化出来的，我在线性代数的教材上没有看到推导过程。可能是作者觉得比较繁琐，所以没有给出来吧。

中心极限定理：

中心极限定理是说，不管一个事件的概率分布是什么，不管它是泊松分布还是二项式分布还是超几何分布还是什么分布，只要你这个事件发生的次数足够多，这些事件的总和就是正态分布（我这么说不太严谨，大致是这个意思）。这个东西理解起来非常简单，也非常直观，就是说正态分布就是一个很“正”的分布，所以不管什么分布，发生次数足够多的时候，都近似是个正态分布。

但是它的证明过程挺复杂的，我不知道咋证出来的。

虚数：

虚数这个东西，看起来很简单，就是解这种方程的时候发现无解了，但是我们又希望一个一元二次方程有两个解，所以我们就给它整出来一个解吧。那就定义有虚数这么个东西，虚数单位是i，，这样任何一个一元二次方程都有两个解了。这个虚数怎么理解呢？就是在坐标轴上，加上一个垂直于实数轴的坐标轴，叫虚轴，虚轴上的数都是虚数。

看起来非常简单，而且非常好理解，一个初中生都知道。但是历史上的虚数可不是这么来的，历史上的虚数是人们解一元三次方程的时候，发现有时候我们解出来的数字是实数，但是它是两个虚数加起来的：

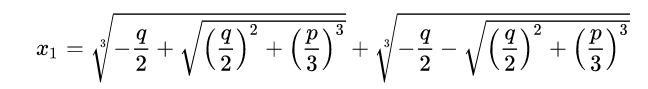
比方说上面这个求根公式（它只是其中一个根），有时候两个根号下面都是有虚数的，但是它加起来却是一个实数。虽然最后结果是个实数，但中间过程产生了虚数，产生了根号下有负数这种理论上不应该存在的东西，还是让人很费解的。很多人理解不了这个东西，但是又无可奈何地接受，后来经过很多数学家的努力才完善了虚数相关的概念。

下面言归正传，讲四元数。

四元数的起源：二维旋转扩展到三维

首先讲讲人们为什么要搞出四元数这么个玩意。

一开始人们为什么要搞出四元数这个东西呢？这个东西是数学家哈密顿搞出来的。先讲讲复数，毕竟四元数是从复数扩展出来的。当时人们知道复数（实数+虚数）是可以表示旋转的，比如一个数字乘i就相当于它在坐标轴上的位置逆时针旋转90度。

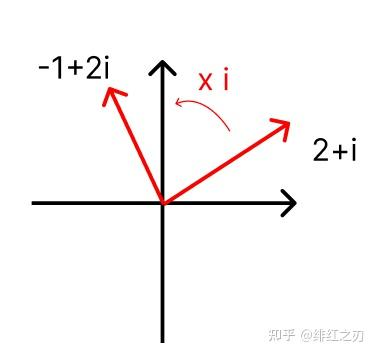
复数和二维旋转

更进一步，复数乘法是可以表示缩放的，比如一个复数乘另一个复数x，相当于缩放一个倍数，再旋转一个角度。这个缩放倍数，就是x的模长（模长就是这个数字到原点的距离），这个旋转角度，就是x到x轴正方向的角度，比如说：

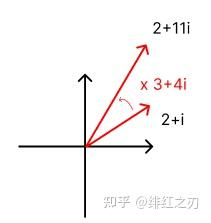
一个数字乘3+4i，就相当于这个数字放大到原来的5倍，再逆时针旋转度。

这是二维空间上的旋转。

三维旋转的常规办法

那么我们怎么表示三维空间上的旋转呢？有两个办法：

1）一个直观的办法是，绕x轴旋转多少度，然后再绕y轴旋转多少度，再绕z轴旋转多少度（实际上绕两个坐标旋转就可以表示所有类型的旋转了）。但是这样有个问题是，得旋转两次。而且这种旋转方式有个问题，就是“万向节死锁”，就是三个旋转轴在某种情况下会“退化”为两个旋转轴。这个有很多视频讲这个，我用文字讲的话不太直观，你找个视频看，一看就懂了。

2）还有个办法是，绕某个轴旋转，比如说绕旋转（那个数字已经单位化了），这样也是可以把它算出来的，写成向量点乘、叉乘、加法组合的形式（v向量绕u向量旋转到了v'向量）：

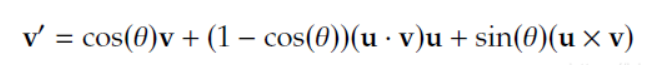
但是这样有点繁琐。

有没有什么办法写成那种，我乘一个数字，相当于在三维空间中旋转呢？就像二维旋转，相当于乘一个复数，那么三维旋转，能不能写成乘一个“超复数”呢？

“表示三维旋转的‘超复数’”

如果你想到了这里，说明你上道了，哈密顿当年也是这么想的。他一开始的想法是，复数是一个实部加上一个虚部，构成两个轴，那么我只要再加上一个轴，就是能在三维中旋转的“超复数”了。于是他就想，要搞出这种的数字：

其中，

那么，请问等于多少？我们给左乘i，它等于-j，右乘j，它等于-i。

第一个问题

如果等于i，那么左乘i等于-j，而i左乘i等于-1，矛盾。

如果等于j，那么右乘j等于-i，而j右乘j等于-1，矛盾。

如果等于1，那么左乘i等于-j，而1左乘i等于i，矛盾。

如果等于-1，那么左乘i等于-j，而-1左乘i等于-i，矛盾。

什么意思呢？就是我们先假设等于一个数字，但是不管假设等于多少，它左乘i或者又乘j以后都会出问题。也就是，等于几都不对。所以三维中的超复数好像造不出来。

第二个问题

三维中的超复数其实还有第二个问题，这个问题来源于“毛球定理”。先说说二维中的旋转：我们用复数乘法来旋转二维上的单位圆，为了简单，我们就只考虑旋转不考虑缩放，就是我们只考虑乘模长为1的复数，我们乘一个复数，单位圆上的所有点都会旋转，比方说我们乘，就相当于单位圆上的所有点都旋转60度，也就是，所有的点都离开了原来的点。

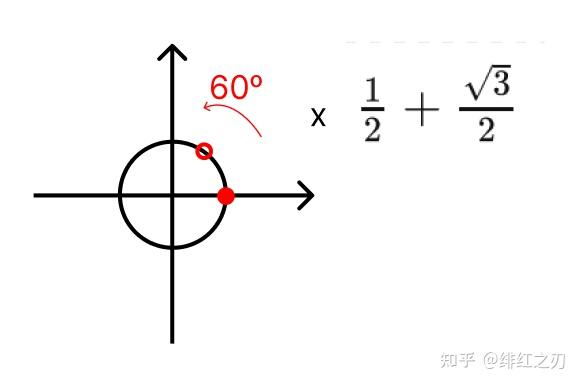
想象一下这个二维的单位圆上有一圈毛，我们用梳子来梳它，我们是可以把单位圆上的所有毛都理顺了的，就是下面这样：

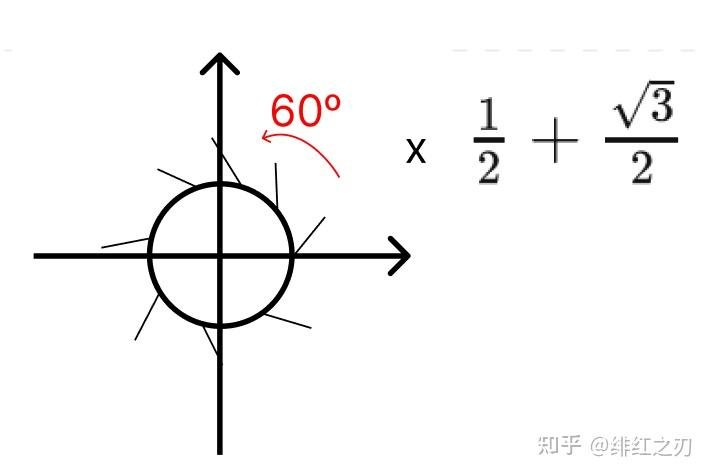
在三维中行不行呢？答案是不行。如果一个三维中的单位圆（就是单位球的球面）上长满了毛，我们用梳子刷它，我们不可能把所有点都理顺，总会有两个点是我们无法理顺的。这个叫“毛球定理”：

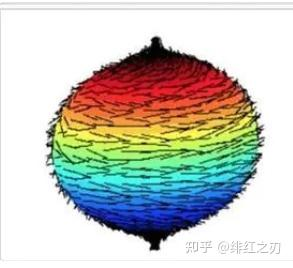
也就是，如果我们想乘以三维中的一个超复数，让所有的点都旋转一定角度，也就是离开原点，那么毛球定理告诉我们：这是不可能的，总有两个点是没法移动（没法被旋转）的。这个你感受一下就好了，我这么说其实也不严谨。

为什么呢？我不知道这个东西怎么证，要证这个东西的话估计也挺繁琐的，我就给一个直观上的理解吧：

我们能够“完美”地在二维中旋转，那么从二维扩展到三维的时候，增加一个维度，那一个增加的维度还不足以旋转起来，换句话说就是我们只加了一个维度，这个维度没法转（想想你怎么能在一维中旋转呢？你是转不起来的）。想象一下，我们转一个圆盘：

我们把二维旋转扩展到三维的时候，相当于从上往下增加了一个维度，那么我们把这个圆盘从上往下摞：

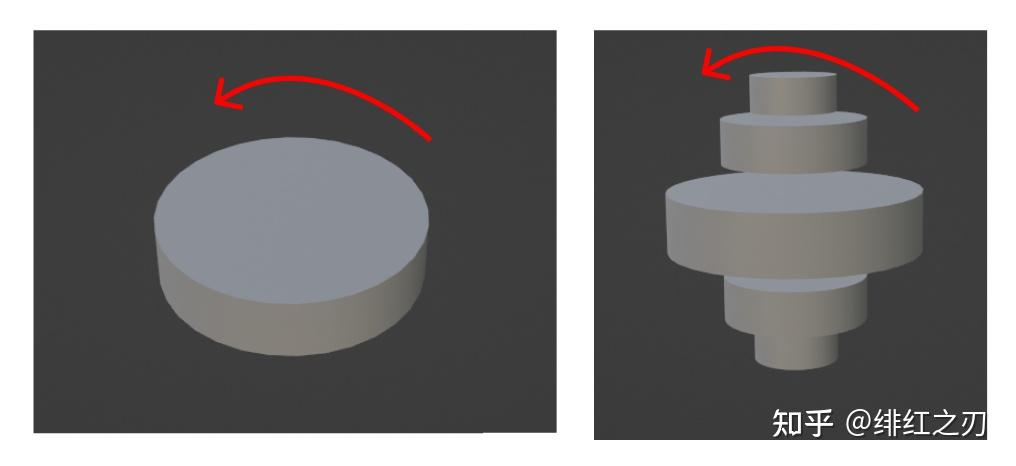
然后一起逆时针转那堆圆盘。那堆圆盘合起来看，就有点像个三维中的单位圆了。每个圆盘的边缘区域，就是三维中单位圆上的面。你可以想象，如果我们把圆盘摞的特别的密，那么最上面和最下面那个圆盘的边缘区域挨的太近了，就几乎不动了。

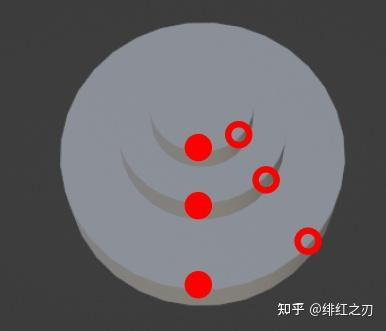
什么意思呢？就是上面这个图中，越靠上的圆，旋转一个角度后，红色实心和红色空心挨的越进，那么显然，最上面的那个圆是小到了极致的，红色实心和红色空心会几乎贴在一起，也就是，它“转不动”了。

这其实就是毛球定理的另一种理解（这个理解方式是我自己编的，不知道合理不合理，如果不合理的话你可以在评论区指出）。

四元数：四维中的旋转

先推荐一个B站上的视频：三维旋转需要经过四维空间？关于四元数_哔哩哔哩_bilibili我找了知乎、B站、百度上的资料，这个视频是我心目中最直观、易于理解的视频，但我个人还不是非常的满意。

刚才说了，用三个维度的超复数（x=a+bi+cj）表示三维旋转是行不通的，有两个证据：第一个证据是，你没法处理i乘j，因为i乘j等于几都不行；第二个证据是，因为“毛球定理”，你不可能在三维中构造一种旋转，让一个三维的单位球上所有点都转起来。所以，用三维中的超复数表示旋转是行不通的。那就用四维中的数来表示吧，也就是搞出来一个四元数：一个实轴加上三个虚轴：

这玩意的运算怎么定义呢？

那么，ijk这三个数字互相乘等于多少呢？可以这么定义：

这个怎么理解呢？就是你看三维的XYZ坐标轴，我们看右手系，你把X转到Y轴，Y转到Z轴，Z转到X轴，这个轴是“不变”的（当然我这么说不严谨，你大概理解就好），就是说三维中的物体做刚体变换，你把XYZ轴转到了YZX轴，你完全可以“等价”地表示这个物体（当然我这里用等价这个词其实很不严谨，你大概理解就好）。我刚才写的ijk的三个式子，就是相当于把XYZ三个坐标给转了一下。

再加上一条：

你可以检查一下，这回这4个式子是没问题的，不会推出什么矛盾的情况。

因为四元数乘法不满足交换律（这个下面会讲到），所以不等于，最简单的做法就是让它们等大反向吧，然后可以顺理成章地补充出以下几条运算规则：

四元数乘法不满足交换律

首先说一个东西，就是四元数乘法不满足交换律，就是a乘b不等于b乘a。这个怎么理解呢？从旋转的角度来理解：

在二维中，旋转是满足交换律的，你逆时针旋转60度，再顺时针旋转60度，所有点都能转回来。这个东西可以类比微积分当中的环路积分为0的情况，或者类比物理学当中的无旋场（比如电场、引力场），无旋场就是转一圈以后对物体做功为0。其实这两者是一回事。不过这个你不知道就算了，无所谓，不影响理解。

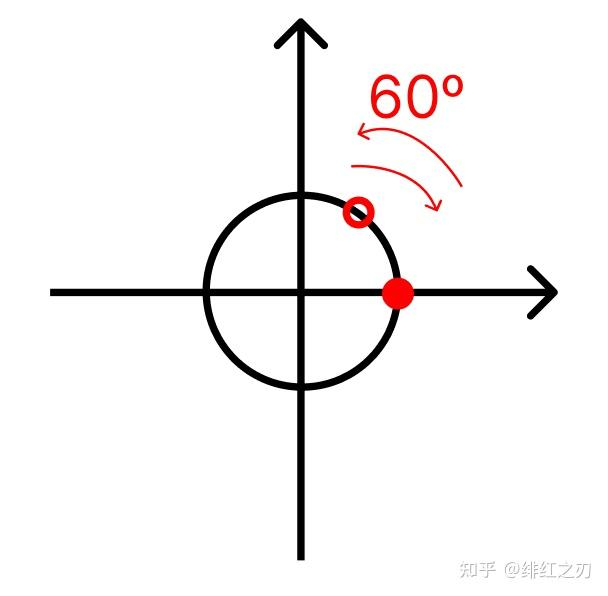
你先转60度，再转30度，和先转30度，后转60度，是一样的。因为你只能向一个方向转。

这对应于复数乘法的运算规律是，复数乘法满足交换律，ab=ba。

但是到三维中就不是这么回事了，一个魔方，你先绕着x轴逆时针转90度，在绕着y轴逆时针转90度，和你先绕y轴逆时针转90度，再绕x轴逆时针转90度，效果是不一样的。这是因为，三维中的旋转，不止一个旋转轴。

四维中的旋转也是这样，旋转顺序交换以后，旋转的那个效果就变了。它对应的四元数乘法运算规律是，四元数乘法不满足交换律，ab不等于ba。

怎么理解四元数

再来说说怎么理解四元数。四元数可以理解为复数的扩展。一个复数，它的实轴单位是1，虚轴单位是i，，这个的一种理解方式是，虚轴上的数字相当于旋转90度，旋转两次就旋转到了180度，转到了实轴上的负半轴。

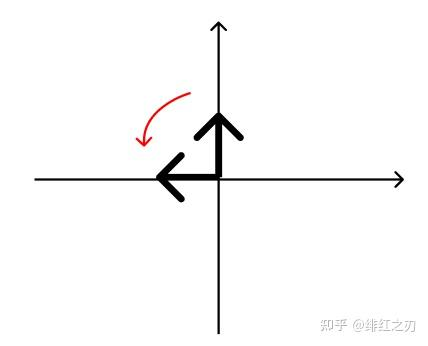
那么，四元数就是把一根虚轴变成了三根，每根都是转两次转到实轴的负半轴。

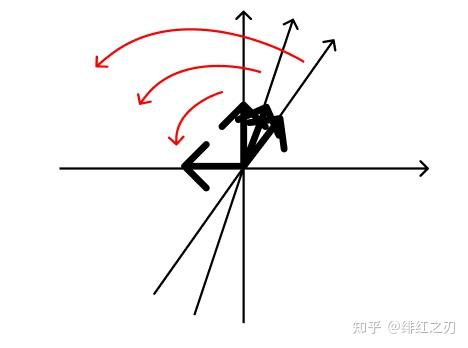
对于复数来说，实轴和虚轴的运算规则是“不平等”的：实轴单位1乘两次以后还是自己，而虚轴单位i乘两次以后到了实轴上。正是因为它们的运算规则“不平等”，所以才能表示旋转。这个是我的一个理解，不太严谨，我也给不出进一步的说明。

对于四元数来说，实轴和虚轴的运算规则也是“不平等”的，跟复数的情况一样。但是，三个虚轴的运算规则是“平等”的。注意这是一个伏笔：一个实轴和其他虚轴是“不平等”的，三个虚轴是“平等”的。

四元数的运算规则

乘法

先说说四元数乘法吧，比如，这两个数怎么乘呢？其实就是全部展开：

当然这只是最笨的展开方式，实际上它可以写成：

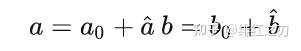
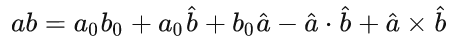
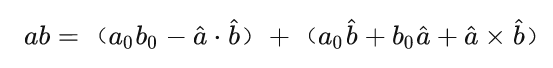
这个东西你只要耐心整理一下就能推出来上面那种“高级”的写法。但我觉得没必要深究，你甚至没必要记那种高级的写法是什么。你只要知道最笨的展开方式是怎么展开的就行了：把每个四元数在四个轴上的值分别相乘，重新合并就行了。

共轭、模长和逆

复数里面有个概念是共轭复数，就是实轴不变，虚轴倒过来，比如的共轭复数是。它们相乘的结果是，这个数字是x的模长的平方，也就是x到原点的距离的平方。

类似，四元数也有共轭四元数，的共轭四元数是，你把这两个数字乘起来，它等于，它也是共轭四元数的模长（x到原点的距离的平方）。

四元数里有个概念叫逆，逆是群论里的一个概念，就是一个东西乘它的逆元等于单位元。我们不扯群论了，我们就举几个例子，比如3+(-3)=0，那么-3可以视为3的逆（在整数加群中，-3是3的逆元，单位元是0），，那么1/3可以视为3的逆（在有理数乘法群中，1/3是3的逆元，单位元是1），线性代数里面非奇异矩阵（方阵）都有逆矩阵。

我们知道，那么显然，所以x的逆。

四元数的乘法、旋转、旋转的“拆分” 四元数乘法可以表示旋转。我们先观察四元数乘法：

左乘、左乘旋转、旋转的“拆分”

我们刚才说了，四元数乘法不满足交换律，也就是左乘一个数和右乘一个数是不一样的。我们对左乘一个数字，我们分别左乘四个轴的单位1, i, j, k，看结果是什么：

我们可以左乘（只有两个轴上有数字），看乘出来个什么东西：

我们观察这个yx，发现yx的1的系数和i的系数都只含x中的a和b，yx的j的系数和k的系数都只含x中的c和d，也就是：yx中的1的系数和i的系数只和x当中的1的系数和i的系数有关，yx中的j的系数和k的系数都只和x中的j的系数和k的系数相关。这么说有点绕，你看下面这个图就懂了：

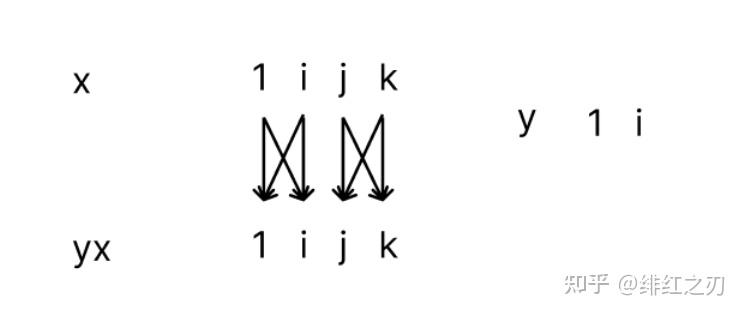
看到这个图，你第一反应是啥？是不是把它分成两部分（下面这样）？

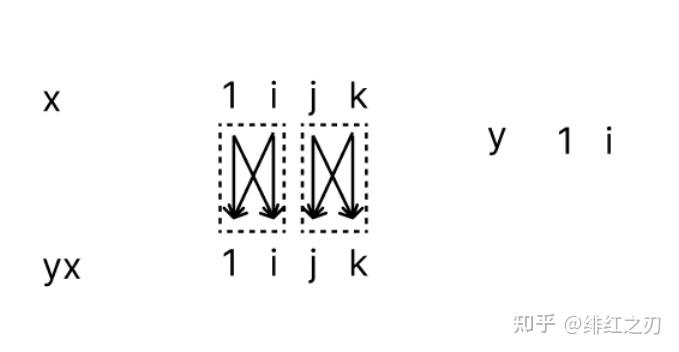
也就是，我们可以把x分成两部分，一部分是1和i，一部分是j和k。之前说，四元数乘法相当于旋转，那么x左乘y相当于对x进行旋转，这个旋转可以“分解”成两个相互独立的部分，一部分是1和i，一部分是j和k。这么说有点抽象，它具体是什么意思呢？就是这个意思：

你可以观察下yx，它前半部分只含有1，i和x的1，i的系数a，b，它的后半部分只含有j，k和x的1，i的系数c和d。

我们现在把yx拆开看，我们这回这么看：

然后我们就有这么两组式子：

和

看第一组式子，它只有1和i两个轴。而且，它乘出来的结果完全符合复数乘。所以，法这就是我们熟悉的复数乘法！

第二组式子和第一组式子的形式是一样的，我们也看成一组复数乘法。而我们知道，复数乘法相当于旋转，那么第一组式子相当于是1和i构成的二维空间上的旋转，第二组式子相当于是j和k构成的二维空间的旋转：

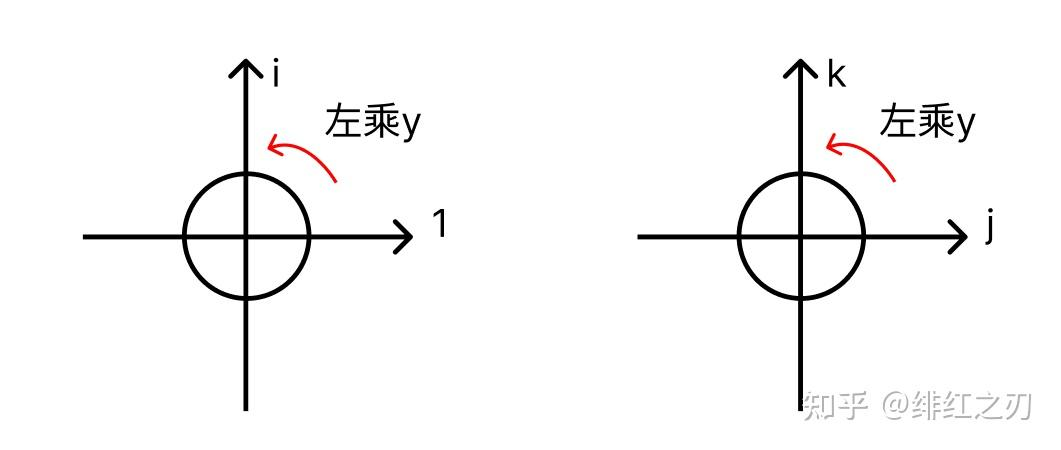
我们把具体的数字放到图像当中：

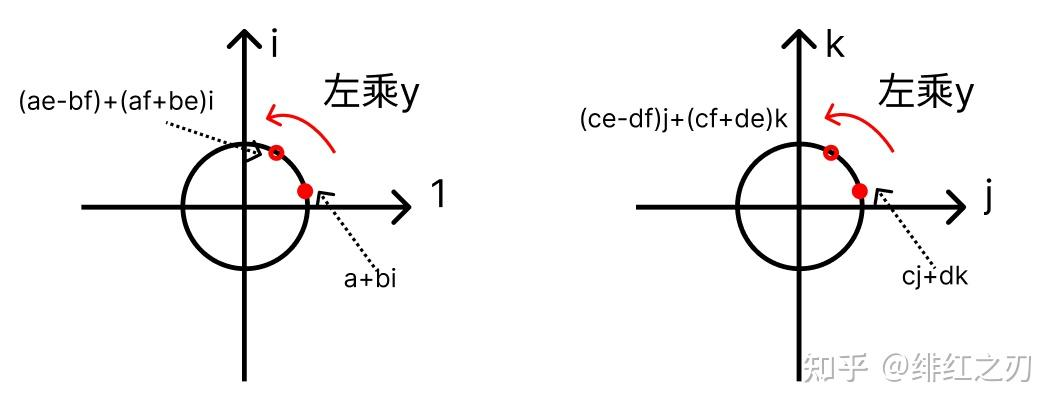
这样，我们就把四元数相乘拆成了两个复数相乘。

左乘和右乘

刚才是x左乘y，我们现在算x右乘y：

我们来对比一下xy和yx的区别：

1和i前面的系数一样，j和k前面的系数不太一样。同样，我们可以把x拆成两部分，xy拆成两部分，然后图像也是两部分图像。不同的是，我们把右乘的图像的j和k要换一下。为了对比，我们同时放上左乘和右乘的图像：

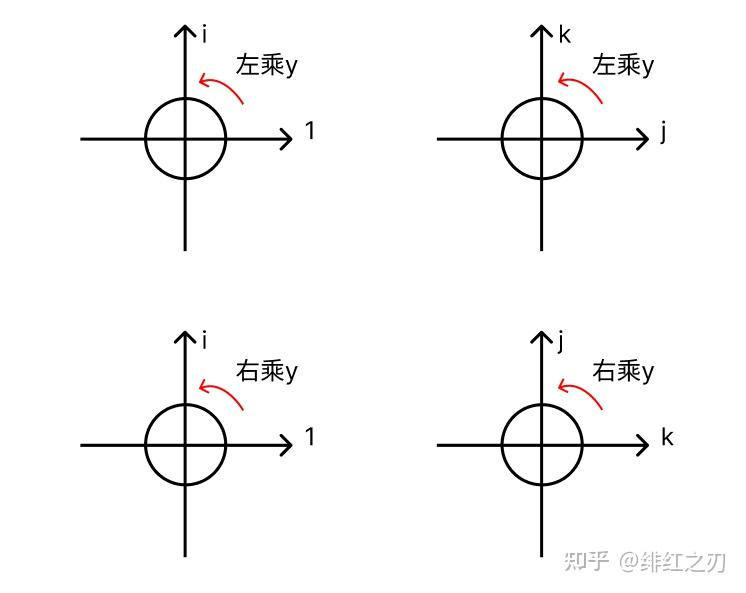
我们为了看着对称，把xy的表达式当中的k和j换个位置，把k放前面，j放后面：

这么一看的话，k和j前面的系数，和1和i前面的系数，就完全对称了。

如果你对数学比较敏感的话，这个时候你应该会感受到一种对称的美。

左乘和右乘的关联、意义

我们再来理解一下左乘和右乘，先把刚才那张图放上来：

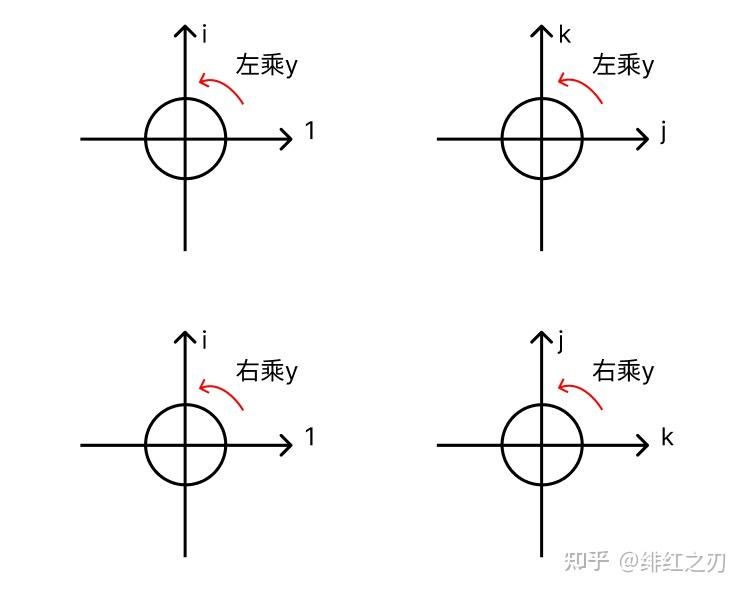
我们把j和k的位置都放成一个位置，这个图就变成了这样：

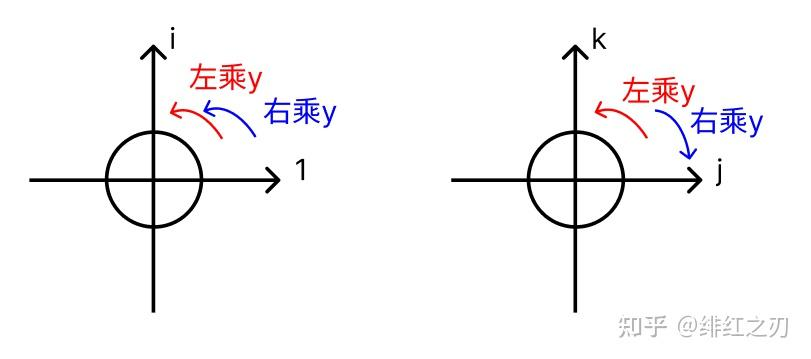
这么看的话就很明朗了：在i和1构成的这个平面上，左乘和右乘是相互“叠加”的效果，而在j和k构成的这个平面上，左乘和右乘是相互“抵消”的效果。

我们把四维空间理解为两个二维空间的叠加，那么左乘的意义就是，第一个二维空间逆时针旋转，第二个二维空间逆时针旋转，右乘的意义就是，第一个二维空间逆时针旋转，第二个二维空间顺时针旋转。

“四维=二维圆盘1+二维圆盘2”

我们搞点有意思的东西吧，做个思想实验：想象一下四维空间，先在四维空间上放一个二维圆盘。它占据维度1和维度2。

这个圆盘占了两个维度了，还剩下两个维度。正好可以放一个新的圆盘。它占据维度3和维度4。

注意，这两个圆盘，分别占据了四维中的不同的维度，所以这两个圆盘所在的空间是完全没有交错的。

如果你对维度1和维度2这两个维度（一个二维平面）进行旋转，这时候第一个圆盘是跟着进行旋转的，而第二个圆盘不受任何影响。如果你对维度3和维度4进行旋转，第二个圆盘旋转，第一个不受任何影响。

那么四维空间中的旋转，就是同时按住这两个盘子进行旋转，有两种旋转方法，第一种方法是，第一个和第二个盘子都逆时针旋转，第二种方法是，第一个逆时针，第二个顺时针。

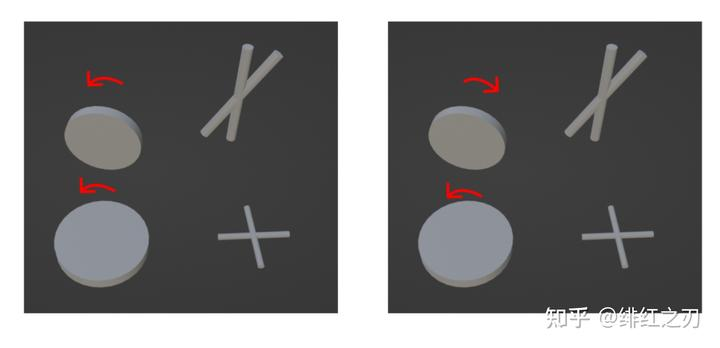
同时旋转两个平面？只旋转一个平面？

不管是左乘还是右乘，都是同时旋转两个平面。那么我们能不能只旋转一个平面呢？当然是可以的，只要我们同时左乘和右乘，那么第一个平面就旋转了两次，而第二个平面两次旋转等大反向，完全抵消。这样就只旋转了一个平面。

就好比你转盘子玩，两个盘子一起转。第一种转法是，左右两个盘子一起逆时针转，第二种转法是，左边的逆时针，右边的顺时针，那你只要先按第一种转法转一下，再按第二种转法转一下，第二个盘子就被转回来了，而第一个盘子被转了两次。

也就是，

当然，我们也可以让第一个盘子不转，第二个盘子转两次，那就是，先左乘y，然后右乘y的共轭四元数，直接给图：

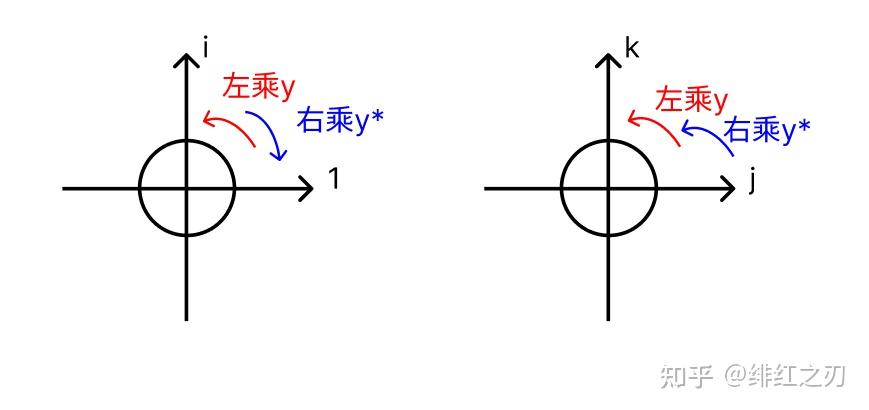
四元数乘法用于三维旋转——铺垫

我们干这么几个事情：

1，把我们刚才得出的结论推广一下：刚才说过，我们对一个向量x=a+bi+cj+dk，先左乘y=e+fi，然后右乘y，相当于在1和i构成的平面上旋转，而在j和k构成的平面上不旋转。我们把这个结论推而广之，假设这个y只有两个轴是有值的，另外两个轴没有值，那么左乘y然后右乘y相当于在这两个轴构成的平面上旋转，而另外两个轴构成的平面不旋转。

如果想让y的两个轴构成的平面上不旋转，而在另外两个平面上旋转，那就先左乘y，然后右乘y的共轭四元数，也就是

2，当用四元数表示三维旋转时，我们用三个虚轴表示三维空间的三个维度，实轴是0。因为三个虚轴的运算规则是“平等”的，所以我们用三个虚轴来表示三维空间的三个维度。

3，假设我们要算向量v绕着向量u旋转度，得到新的向量v'。

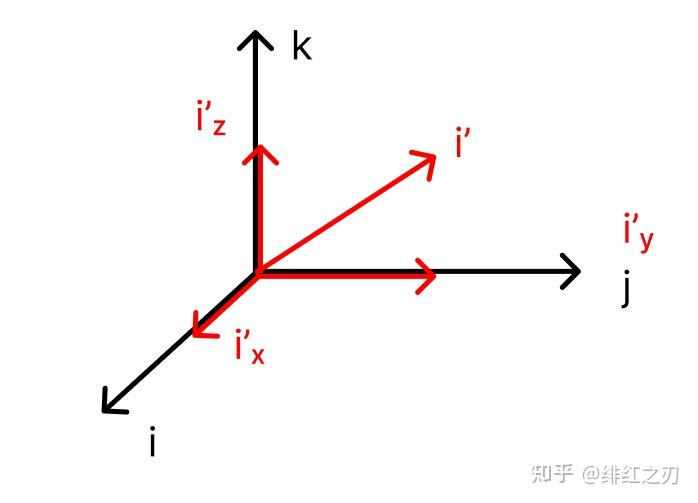
我们可以想象一下，四元数的四个轴，1, i, j, k，我们通过旋转ijk三个轴，变成i', j', k'，让i'转到u的那个方向上。那么，在1, i', j', k'四个轴上，u只在1和i'对应的轴上有值，而在另外两个轴上没有值。

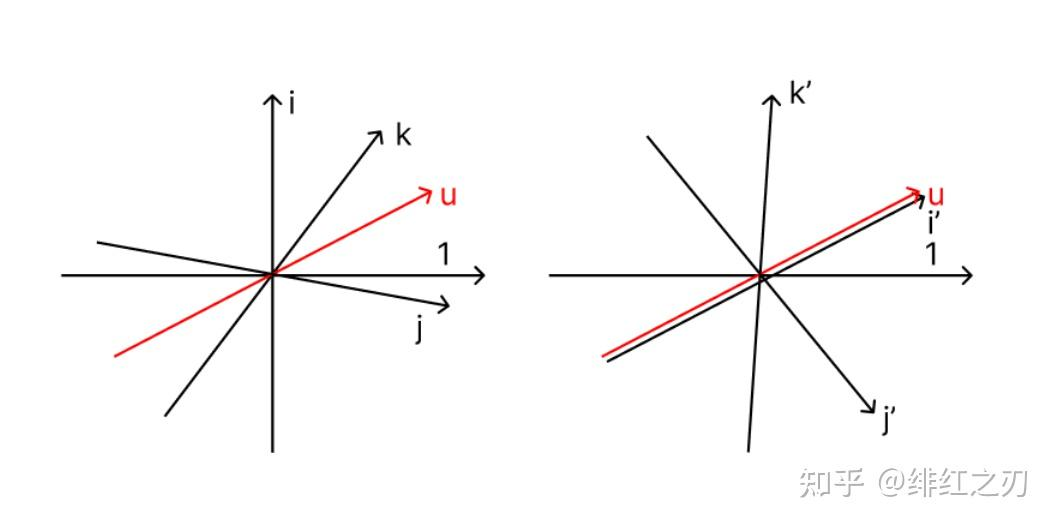
而我们知道，1, i, j, k四个轴构成的空间和1, i', j', k'四个轴构成的空间是等价的。所以我们在第1点中说的结论，对u和v也是成立的。

4，向量v绕着向量u旋转度，得到新的向量v'。根据上一点的结论，我们可以把u放在两个轴上：一个轴是实轴（也就是三维空间中不存在的轴，v和v'在这个轴上的值都是0），另一个轴是u向量所在的轴（也就是把u向量作为一个轴）。另外两个轴，就是跟这两个轴都正交的轴。也就是把u向量作为i'，另外两个轴就是j'和k'了。实轴和u向量所在的轴正交，下面说下它为什么正交：

实轴和三个虚轴都是正交的，那么，把三个虚轴组合起来的一个轴，和实轴也是正交的，因为：

当然我只是大概说明一下，这不算什么严谨的证明。

刚才说，向量v绕着向量u旋转度，得到新的向量v'。那么，我们绕u旋转相当于是乘一个四元数（准确讲叫相当于左乘一个四元数再右乘一个四元数），设这个跟u有关的四元数是q（也就是q和u是对应的）。我们设绕u轴旋转对应的操作是，左乘q或者右乘q或者左乘q或者右乘q。

向量v是三维空间中的向量，而我们要把它放到四维当中旋转，所以说有一个轴空出来了。我们让实轴空出来吧，v的实轴的值是0，三个虚轴的值是三维空间中三个坐标的分量。为什么让实轴空出来呢？因为刚才说了，实轴和三个虚轴的运算规则不等价，而三个虚轴彼此等价，所以我们把v的三个维度放在三个虚轴上，让它们三个维度等价。

向量v'也是三维空间中的向量，所以v'的实轴的值也是0。

由于v和v'实轴上的值都是0，所以v变到v'的过程中，实轴对应的值不变，而u向量所在的轴对应的值也不变（解释一下：因为是绕u向量转的，所以v和v'在u向量上的分量是一样的）。我们找到了两个不变的轴：实轴和u所在的轴，它们构成了一个平面。这个平面不变。而另外两个轴对应的平面是变的。

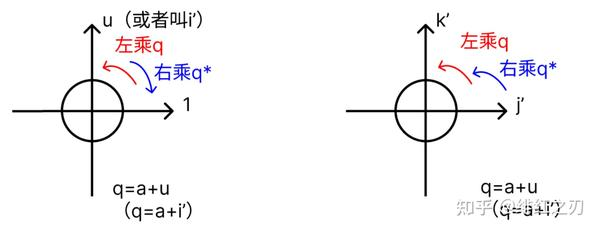
于是，对于向量v绕着向量u旋转度，得到新的向量v'，有（注意q和u是对应起来的）v左乘q再右乘q*以后的结果是，q所在的两个轴（实轴，和q所在的轴也就是u向量所在的轴）的值不变，而另外两个轴（就是两个虚轴j'和k'）上的值变了。

四元数乘法用于三维旋转

刚才铺垫完了，现在可以开始正文了。其实铺垫做到位以后，正文就是那么一点点。

刚才我们得出一个结论，就是对于向量v绕着向量q旋转度，得到新的向量v'，有。我们只是没有解释，这个v是个什么，q是个什么。由于向量v存在于三维，所以向量v的实轴是0，虚轴就是向量v投射到xyz三个坐标轴的分量，也就是。同理，由于向量q存在于三维，所以向量q的实轴是0，虚轴就是向量q投射到xyz三个坐标轴的分量，也就是。所以，向量v和向量q全部退化为三维中的数字，它们相乘的结果，退化为“三元数”相乘……

等等，出问题了。我们刚说完用三维中的数字没法表示三维旋转，这里居然退化成“三元数”了。那么肯定是我某一步写错了。

请你思考几秒钟，看能不能发现是哪里的问题。

q和v哪一个是“真正的四元数”

-------------公布答案--------------------

是q写错了。我们不可能让v和q的实轴都是0，否则的话，q和v相乘就真的退化为“三元数”了。q和v中，谁的实轴不应该是0呢？答案是q。先把刚才这个图放出来：

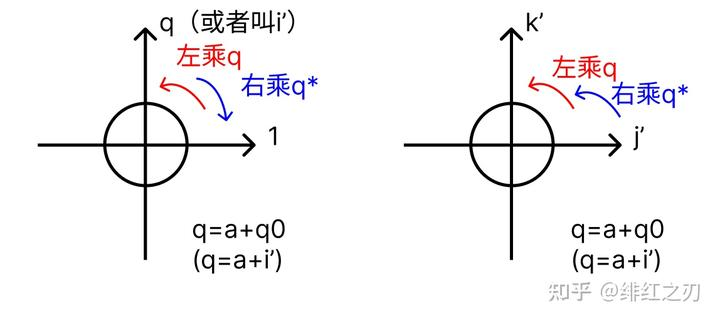
我们把q的四个轴：1, i', j', k'分成了两部分，分别构成两个平面，它在第一个平面上是转过去又转回来了，也就是，就算它有值，它也在两次旋转中抵消掉了。所以，q的实轴上有值其实是一件无所谓的事情，反正转两次以后就抵消掉了。我们令，然后，根据刚才的说法，通过旋转ijk轴，把q的方向和i'轴重合，这样j'和k'的值就是0了。再把刚才那个图放出来（这回就放小图了）：

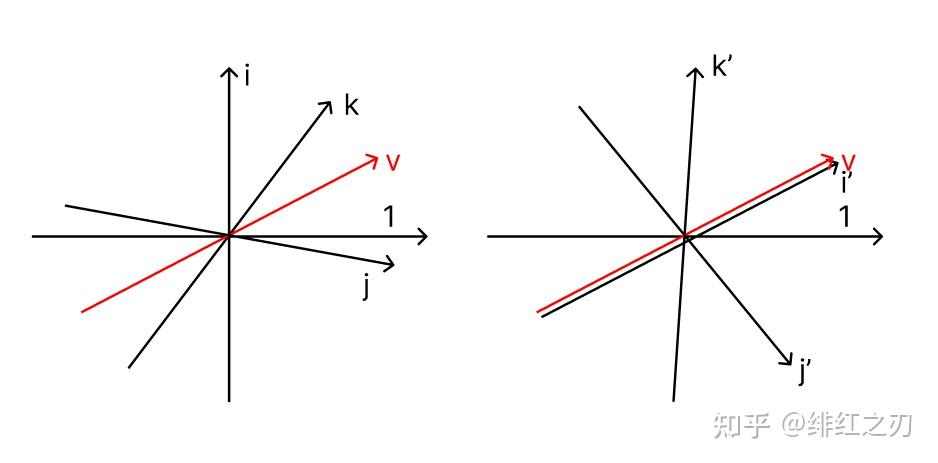
也就是，，由于i'是从ijk转出来的，所以比对一下各个分量的值，，由于旋转完以后模长（向量到原点的距离）是不变的，所以有，化简后有。这个东西怎么理解呢？就是q在ijk三个轴上的分量，相当于是i'上的值投影到ijk三个值上的分量（或者说ijk三个轴上的分量合并到了i'这个轴上）：

q和v具体是什么

对于向量v绕着向量u旋转度，得到新的向量v'，有 (q和u是对应的），这个q和v具体是什么呢？

刚才我们得到一些阶段性的结论：

1，v的实轴是0，q的实轴不是0，所以可以写成 ,

2，我们可以通过旋转，把i, j, k轴转到i', j', k'轴，使得i'正对着q向量在三个虚轴上的那部分。那么，i'上有值，而j'和k'上没有值。那么，q可以写成，其中，它们满足，q在ijk轴上的值就是q在i'轴上的值在ijk三个轴上的投影。

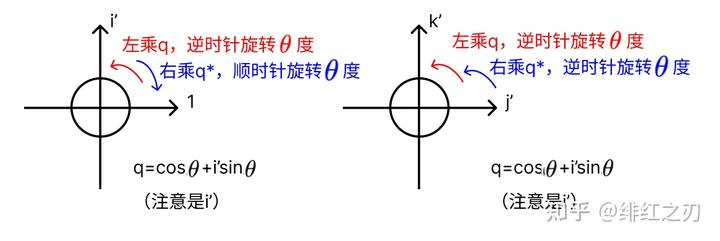
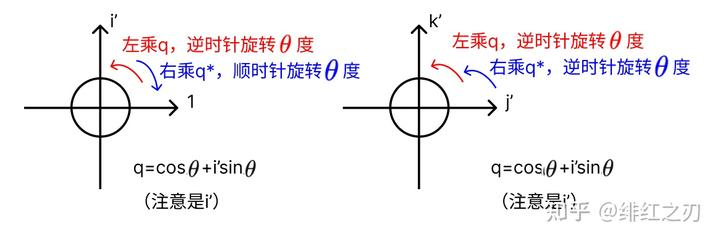
现在我们来类比一下用复数表示的二维旋转：假设我们要把二维向量v0逆时针旋转度，得到新的向量v0'，那么，也就是相当于令，那么

我们现在令（注意是i'），然后，它的效果是，j'和k'轴所在平面上逆时针旋转度。因为我们最后要转的是度，所以我们一次转度，这样转两次就转够了。

所以真正的，因为，所以。是它的共轭四元数，所以，展开以后是：

，其中是在xyz三个坐标轴上的投影。

这个q是单位化的，也就是模长是1。因为绕u旋转的时候，u的方向对旋转有影响，u的模长（大小）对旋转没有影响。所以为了方便，就把u对应的四元数q给单位化了。

具体运算：举例子

对于向量v绕着向量u旋转度，举个例子，比如v是，u是，是60度，先对u单位化：，然后把角度化成弧度，，然后算q，

然后把这三个东西乘起来，至于怎么乘，就用我前面说的四元数乘法运算（把所有项分别相乘再相加），或者用那种把四元数写成标量+向量的乘法（但本质上运算过程是一样的），还有把四元数乘法写成矩阵形式的，但是我这里没必要写了，我觉得这里没必要继续把问题搞复杂。但总之你会算这个东西了。

后记

四元数的用途和好处

实数是一个轴上的数字，复数是两个轴上的数字。四元数是四个轴上的数字，这种比复数更复数的东西，我们叫它“超复数”，看起来就是超级复数的意思。四元数这个东西，比较常见的用处有两个：一个用处是计算机图形学中的应用，它的一个常见应用是游戏引擎中用四元数表示三维旋转；另一个用处是量子力学中，量子有两个自旋方向，人们用四元数来表示量子自旋。

先不说量子自旋，毕竟量子力学太抽象，离我们生活有点远，而且我也不太懂，就说说这个计算机图形学上的应用。我们怎么表示旋转呢？人们一开始是用欧拉角表示旋转，就是我先绕x轴旋转多少度，再绕y轴旋转多少度。但是这种方法会导致万向节死锁的问题，也不方便插值运算。人们发现如果用四元数表示旋转，就没有万向节死锁的问题，也方便插值运算。

而且，四元数表示旋转，经过某些简化以后，运算量还变小了。

其实为什么没有万向节死锁，就显而易见了：四元数处于四维空间中，四维空间中的旋转更加的“灵活”：我们完全可以用左乘或右乘一个数字，来“完美地”表示整个四维空间中的旋转，而不会出现三维空间中“毛球定理”那种有的点没法旋转的情况。

至于说为什么容易插值，这个我就不清楚了。没太深究。

超复数

一个轴上的数字叫“实数”，两个轴上的数字叫“复数”，更多轴上的数字，就叫“超复数”，顾名思义，超级复数。四元数是最简单的超复数，除此之外还有八元数、十六元数。八元数和十六元数都是用在量子力学上面。

数学成果的兴起

四元数这个东西是什么时候火起来的呢？是不是哈密顿一开始搞出来这个东西的时候，它就火了呢？不是的。哈密顿一开始搞出四元数的时候，大肆推广，还成立了个四元数小组来推广它，但是并没有受到广泛的应用，而且反对者们也没闲着：他们说四元数是“邪恶的数字”，说它没有必要创造出来，传说电影《爱丽丝漫游仙境》里的疯帽子就是在影射哈密顿和他搞出来的四元数。过了很多年以后，计算机出来了，计算机图形学出来了，人们发现三个维度中的数字表示旋转的时候不方便，四元数表示旋转很方便，这时候四元数才火起来。

也就是，数学上的很多东西，当它有了实际应用之后，才会被人们广泛接受。比方说微积分就是牛顿在研究物理问题的时候搞出来的，格林公式、高斯公式（通量和散度）、斯托克斯公式（旋度）就是解决电磁学、流体力学中的一些问题搞出来的。这就是数学和技术发展之间的关系。

投稿作者为『自动驾驶之心知识星球』特邀嘉宾，欢迎加入交流！

① 全网独家视频课程

BEV感知、毫米波雷达视觉融合、多传感器标定、多传感器融合、多模态3D目标检测、车道线检测、轨迹预测、在线高精地图、世界模型、点云3D目标检测、目标跟踪、Occupancy、cuda与TensorRT模型部署、大模型与自动驾驶、Nerf、语义分割、自动驾驶仿真、传感器部署、决策规划、轨迹预测等多个方向学习视频（扫码即可学习）

网页端官网：www.zdjszx.com

② 国内首个自动驾驶学习社区

国内最大最专业，近3000人的交流社区，已得到大多数自动驾驶公司的认可！涉及30+自动驾驶技术栈学习路线，从0到一带你入门自动驾驶感知（2D/3D检测、语义分割、车道线、BEV感知、Occupancy、多传感器融合、多传感器标定、目标跟踪）、自动驾驶定位建图（SLAM、高精地图、局部在线地图）、自动驾驶规划控制/轨迹预测等领域技术方案、大模型、端到端等，更有行业动态和岗位发布！欢迎扫描下方二维码，加入自动驾驶之心知识星球，这是一个真正有干货的地方，与领域大佬交流入门、学习、工作、跳槽上的各类难题，日常分享论文+代码+视频