JAVA-爬楼梯

题目：

有一座高度是10级台阶的楼梯，从下往上走，每跨一步只能向上1级或者2级台阶，要求用程序来求出一共有多少种走法？

例子，每次走1级台阶，一共走10级台阶，这是其中一种走法，我们可以简写成 1,1,1,1,1,1,1,1,1,1

解题思路：

假设你只差最后一步走到10级台阶，这时候会出现几种情况？
这时只会出现两种情况，

• 第一种：最后一步走1级台阶，第一种情况对应的是已经走到了第9级台阶
• 第二种：最后一步走2级台阶，第二种情况对应的是已经走到了第8级台阶

此时并不具体考虑如何走到第9或者第8级台阶的

假设走到第10级台阶的走法有F(10)
则走到第9级台阶的走法有F(9)
则走到第8级台阶的走法有F(8)
则F(10)=F(9)+F(8)
由题意可知
F(1)=1
F(2)=2

解法一：常规的迭代算法

public static int getClimbingWays(int n) {
        if (n < 1) {
            return 0;
        }
        if (n == 1) {
            return 1;
        }
        if (n == 2) {
            return 2;
        }
        return getClimbingWays(n - 1) + getClimbingWays(n - 2);
    }

存在的问题：

此计算过程类似一颗二叉树，顶点是F(10),左右子节点是F(9)和F(8)，依次计算下去，这个二叉树层高10-1，节点个数2^10-1，
时间复杂度近似O(2^n)
这一颗计算二叉树中有许多重复的计算部分,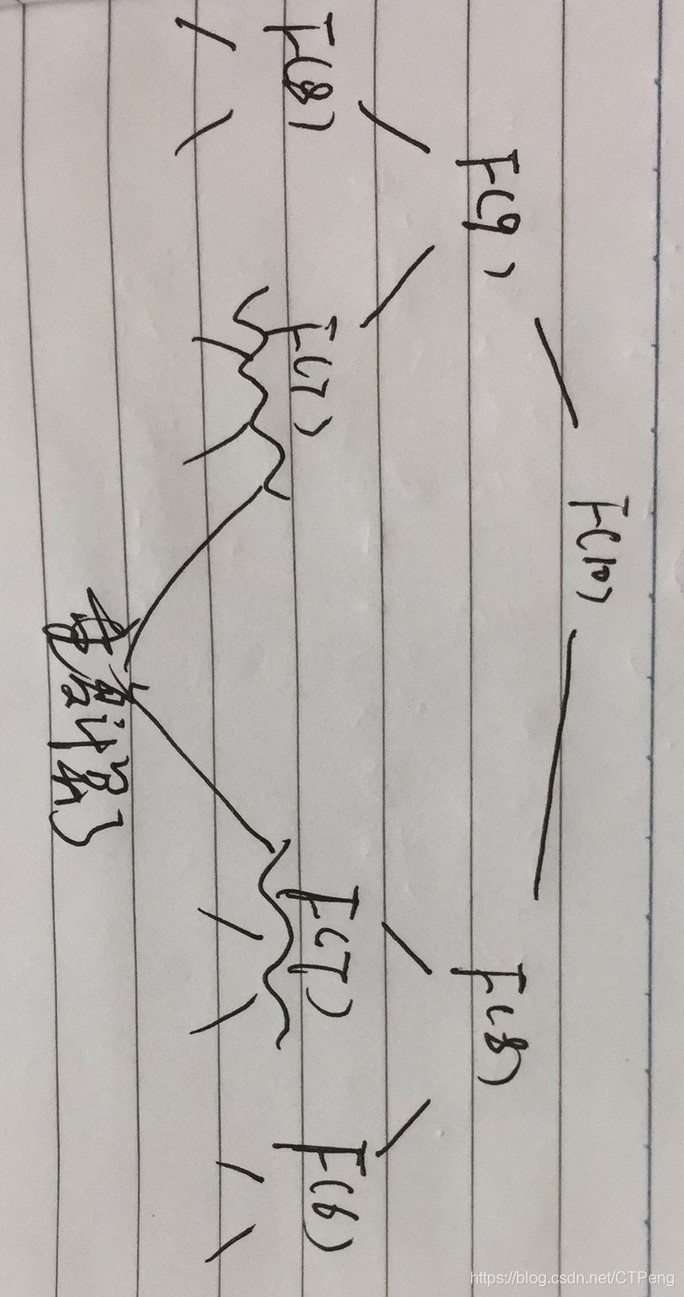
这些重复的部分事实上我们可以采用缓存将其保存起来

解法二：采用缓存的方式，以降低时间复杂度

具体实现如下：

public static int getClimbingWaysCache(int n, HashMap<Integer, Integer> map) {
        if (n < 1) {
            return 0;
        }
        if (n == 1) {
            return 1;
        }
        if (n == 2) {
            return 2;
        }
        if (map.containsKey(n)) {
            return map.get(n);
        } else {
            Integer value = getClimbingWays(n - 1) + getClimbingWays(n - 2);
            map.put(n, value);
            return value;
        }
    }

在以上代码中，集合map是一个缓存。当每次需要计算F(N)的时候，会首先从map中寻找匹配元素。如果map中存在，就直接返回结果，如果map中不存在，就计算出结果，存入缓存中。
此时时间复杂度：O(n)，需要计算F(10),F(9),。。。这些数字
此时空间复杂度：O(n)，需要保存F(10),F(9),.。。。F(3),由于F(1)和F(2)都是已知的不需要缓存在备忘录中

问题

这种方法中所需要的空间复杂度为O(n)，这种计算方法采用的自顶向下的计算方式，所以必须保存每次计算的结果，以便后期取用。如何降低空间复杂度？

解法三：采用自底向上算法，以降低空间复杂度

实现

 public static int getClimbingCacheCacheImp(int n) {
        if (n < 1) {
            return 0;
        }
        if (n == 1) {
            return 1;
        }
        if (n == 2) {
            return 2;
        }
        int a = 1;
        int b = 2;
        int temp = 0;
        for (int i = 3; i <= n; i++) {
            temp = a+b;
            a = b;
            b = temp;
        }
        return temp;
    }

程序从 i=3 开始迭代，一直到 i=n 结束。每一次迭代，都会计算出多一级台阶的走法数量。迭代过程中只需保留两个临时变量a和b，分别代表了上一次和上上次迭代的结果，最后的结果由temp保存。
此时时间复杂度：O(n)，需要计算F(10),F(9),。。。这些数字
此时空间复杂度：O(1)，需要保存a,b,temp,所需空间为3（常量）