leetcode 1030. Matrix Cells in Distance Order 解法 python

最新推荐文章于 2024-06-09 21:18:28 发布

原创最新推荐文章于 2024-06-09 21:18:28 发布 · 795 阅读

0 ·

CC 4.0 BY-SA版权

文章标签：

#leetcode #python #算法 #编程

leetcode算法从零到结束专栏收录该内容

112 篇文章

订阅专栏

本文探讨了如何在给定矩阵中，根据Manhattan距离，从指定起始点出发，将所有单元格按距离从小到大的顺序进行排序。提供了解题思路及两种不同算法实现，包括直接计算距离并排序的方法，以及一种更高效的计数排序实现。

一.问题描述

We are given a matrix with R rows and C columns has cells with integer coordinates (r, c), where 0 <= r < R and 0 <= c < C.

Additionally, we are given a cell in that matrix with coordinates (r0, c0).

Return the coordinates of all cells in the matrix, sorted by their distance from (r0, c0) from smallest distance to largest distance. Here, the distance between two cells (r1, c1) and (r2, c2) is the Manhattan distance, |r1 - r2| + |c1 - c2|. (You may return the answer in any order that satisfies this condition.)

Example 1:

Input: R = 1, C = 2, r0 = 0, c0 = 0
Output: [[0,0],[0,1]]
Explanation: The distances from (r0, c0) to other cells are: [0,1]

Example 2:

Input: R = 2, C = 2, r0 = 0, c0 = 1
Output: [[0,1],[0,0],[1,1],[1,0]]
Explanation: The distances from (r0, c0) to other cells are: [0,1,1,2]
The answer [[0,1],[1,1],[0,0],[1,0]] would also be accepted as correct.

Example 3:

Input: R = 2, C = 3, r0 = 1, c0 = 2
Output: [[1,2],[0,2],[1,1],[0,1],[1,0],[0,0]]
Explanation: The distances from (r0, c0) to other cells are: [0,1,1,2,2,3]
There are other answers that would also be accepted as correct, such as [[1,2],[1,1],[0,2],[1,0],[0,1],[0,0]].

Note:

1 <= R <= 100
1 <= C <= 100
0 <= r0 < R
0 <= c0 < C

二.解决思路

这道题规律很明显,类似下图，该图摘自https://leetcode.com/problems/matrix-cells-in-distance-order/discuss/278708/O(n)-with-picture

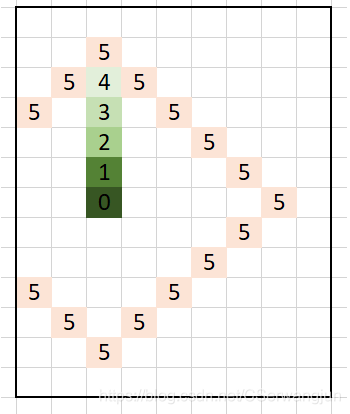
看到这题的第一印象就是从给的点为中心开始，从1距离扩散到R+C-1的距离，一个一个的生成每个点

后面感觉leetcode挺松的，然后接受率这么高，想到真比赛效率第一，就实现了最简单的试试

直接遍历每个点计算距离，然后排序

贴上两个版本

更新一下：后面看到一个不错的实现

计数排序：我们可以看出距离原点的长度是呈连续性增长，每次+1，因此我们只要在迭代计算每个点距离的时候，记录下这个距离下有多少点，一遍迭代后我们知道了每个距离下有多少点，那么我们就可以知道每个距离的起点在哪。然后在第二次算距离，用hash映射过去，附一个实现链接：计数排序java实现

更多leetcode算法题解法请关注我的专栏leetcode算法从零到结束或关注我

欢迎大家一起讨论一起刷题一起ac

三.源码

class Solution:
    #normal version
    def allCellsDistOrder(self, R: int, C: int, r0: int, c0: int) -> List[List[int]]:
        distance=[]
        res=[]
        for i in range(0,R):
            for j in range(0,C):
                distance.insert(i*C+j,(abs(i-r0)+abs(j-c0),i,j))
        distance=sorted(distance,key=lambda x:x[0])
        for m in range(0,R*C):
            res.append([distance[m][1], distance[m][2]])
        return res

class Solution:
    def allCellsDistOrder(self, R: int, C: int, r0: int, c0: int) -> List[List[int]]:
        res=[]
        res.append([r0,c0])
        for d in range(1,R+C):
            for x in range(-d,d+1):
                r1=r0+x;c1=c0+d-abs(x);c2=c0-d+abs(x)
                if 0<=r1<R:
                    if 0<=c1<C:
                        res.append([r1,c1])
                    if 0<=c2<C and c1!=c2:
                        res.append([r1,c2])
        return res