一、最小生成树
最小生成树对应的图一般都是无向图。
1 朴素版Prim算法
I 算法思想
点到集合的距离就是点到集合中的点的距离的最小值，最小生成树的边就是距离集合最近的点t的距离对应的边就是生成树的边。
典型的最小生成树问题：几个城市，给定了城市之间的距离，希望铺公路把城市连通起来，问最短的铺设距离是多少？
II 模板题
#include <iostream>
#include <cstring>
using namespace std;
const int N = 510;
const int INF = 0x3f3f3f3f;
int g[N][N];
int dist[N];
bool st[N];
int n, m;
int prim()
{
memset(dist, 0x3f, sizeof(dist));
int res = 0;
for (int i = 0; i < n; ++i)
{
// 找当前不在集合中的 离集合最近的点
int t = -1;
for (int j = 1; j <= n; ++j)
{
if (!st[j] && (t == -1 || dist[j] < dist[t]))
{
t = j;
}
}
// 如果当前不是第一个点 但是dist[t] == INF 说明不连通
// 就应该返回INF
if (i != 0 && dist[t] == INF) return INF;
st[t] = true;// 入集合
if (i != 0) res += dist[t];// 把这条边加到最小生成树中(如果不是第一个点)
// 更新其他点通过t点到集合的最短距离
for (int j = 1; j <= n; ++j)
{
if (dist[j] > g[t][j]) dist[j] = g[t][j];
}
}
return res;
}
int main()
{
scanf("%d%d", &n, &m);
int a, b, c;
memset(g, 0x3f, sizeof(g));
while (m--)
{
scanf("%d%d%d", &a, &b, &c);
g[a][b] = g[b][a] = min(g[a][b], c);
}
int t = prim();
if (t == INF) puts("impossible");
else printf("%d\n", t);
return 0;
}
II LeetCode1584.链接所有点的最小费用
class Solution {
public:
const int INF = 0x3f3f3f3f;
int prim(vector<int>& dist, vector<bool>& st, const vector<vector<int>>& g)
{
int res = 0;
int n = dist.size();
for (int i = 0; i < n; ++i)
{
int t = -1;
for (int j = 0; j < n; ++j)
{
if (!st[j] && (t == -1 || dist[j] < dist[t])) t = j;
}
if (i != 0 && dist[t] == INF) return INF;
if (i != 0) res += dist[t];
st[t] = true;
for (int j = 0; j < n; ++j)
{
dist[j] = min(dist[j], g[t][j]);
}
}
return res;
}
int minCostConnectPoints(vector<vector<int>>& points)
{
int n = points.size();
vector<vector<int>> g(n, vector<int>(n, INF));
for (int i = 0; i < n; ++i)
{
for (int j = i; j < n; ++j)
{
if (i == j) g[i][j] = 0;
else
{
int distance = abs(points[i][0] - points[j][0]) + abs(points[i][1] - points[j][1]);
g[i][j] = g[j][i] = distance;
}
}
}
vector<int> dist(n, INF);
vector<bool> st(n);
return prim(dist, st, g);
}
};
由于堆优化版本的Prim算法和Dijkstra算法的堆优化版本差不多，并且堆优化版本的Prim算法不怎么用，所以我们就不讲了。
2 Kruskal算法
I 算法思想
算法思路：
这个第二步用的就是并查集！判断是否连通用的就是p(find(a)) != p(find(b))，加入到集合中就是p(find(a)) = find(b).
并查集每次操作的时间复杂度都是O(1)，m条边总复杂度就是O(m)，总体的时间复杂度就是O(mlogm)。
II 模板题
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 2e5 + 10, INF = 0x3f3f3f3f;
// 用一个边的数组来存储图
struct edge
{
int a, b, w;
bool operator<(const edge& e) const
{
return w < e.w;
}
}edges[N];
int p[N];// 并查集
int find(int x)
{
if (x != p[x]) p[x] = find(p[x]);
return p[x];
}
int n, m;
int kruskal()
{
for (int i = 1; i <= n; ++i)
{
p[i] = i;
}
sort(edges, edges + m);
int res = 0, cnt = 0;
for (int i = 0; i < m; ++i)
{
int a = edges[i].a, b = edges[i].b, w = edges[i].w;
a = find(a), b = find(b);
// 检查是否连通
if (a != b)
{
res += w;
++cnt;
// 并且把它们连通起来
p[a] = b;
}
}
// 如果最后边数小于n - 1 说明不连通 没有最小生成树
if (cnt < n - 1) return INF;
return res;
}
int main()
{
cin >> n >> m;
int a, b, w;
for (int i = 0; i < m; ++i)
{
cin >> a >> b >> w;
edges[i] = {a, b, w};
}
int t = kruskal();
if (t == INF) puts("impossible");
else printf("%d\n", t);
return 0;
}
III LeetCode1489. 找到最小生成树里的关键边和伪关键边
先执行一遍Kruskal算法，得到最小生成树与其权值，我们称为原始权值。由于执行最小生成树的Kruskal算法会排序，而结果数组中要原始下标，所以可以在排序前先把原始下标到edge[i]的里头。
遍历一遍边数组，判断每条边是关键边还是非关键边。
判断关键边的方法就是把这条边去掉后，看看执行一遍最小生成树Kruskal算法得到的最小生成树的权值是否大于原来的权值或直接导致最小生成树不存在了，如果满足这种情况，那么这条边就是关键边；否则如果不是关键边，那么要判断它是否为伪关键边，就可以先把这条边优先考虑，入最小生成树集合，然后执行一遍最小生成树Kruskal算法，如果其最小生成树的权值等于原最小生成树的权值，就说明这条边它虽然不是关键边，但是它可以出现在某个最小生成树中，它就是伪关键边。
更多细节见代码注释：
class Unionset
{
public:
Unionset(int n) : p(vector<int>(n)), _n(n)
{
for (int i = 0; i < n; ++i) p[i] = i;
}
int find(int x)
{
if (p[x] != x) p[x] = find(p[x]);
return p[x];
}
void restate()
{
for (int i = 0; i < _n; ++i) p[i] = i;
}
vector<int> p;
int _n;
};
class Solution {
public:
int _n;
int kruskal(const vector<vector<int>>& edges)
{
Unionset u(_n);
int m = edges.size();
int res = 0;
int cnt = 0;
for (int i = 0; i < m; ++i)
{
int a = edges[i][0], b = edges[i][1], w = edges[i][2];
a = u.find(a), b = u.find(b);
if (a != b)
{
res += w;
++cnt;
u.p[a] = b;
}
}
if (cnt < _n - 1) return 0x3f3f3f3f;
return res;
}
vector<vector<int>> findCriticalAndPseudoCriticalEdges(int n, vector<vector<int>>& edges)
{
vector<vector<int>> ans(2);
_n = n;
int m = edges.size();
// 为了后面能找到下标 先把原始下标记录在edges中
for (int i = 0; i < m; ++i)
{
edges[i].push_back(i);
}
// 先求一遍最小生成树的大小
sort(edges.begin(), edges.end(),
[](const vector<int>& e1, const vector<int>& e2)
{
return e1[2] < e2[2];
});
int initval = kruskal(edges);
// 遍历每条边 判断其是否为关键边或伪关键边
Unionset u(n);
for (int i = 0; i < m; ++i)
{
// 判断其是否为关键边
// 方法是再走一次kruskal算法 但是禁止这条边参与
// 看看最后的结果
// 若不连通了或最小生成树的权值变大了 则其为关键边
u.restate();
int curval = 0, curcnt = 0;
for (int j = 0; j < m; ++j)
{
if (j != i)
{
int a = edges[j][0], b = edges[j][1], w = edges[j][2];
a = u.find(a), b = u.find(b);
if (a != b)
{
curval += w;
++curcnt;
u.p[a] = b;
}
}
}
if (curcnt < n - 1 || (curcnt == n - 1 && curval > initval))
{
ans[0].push_back(edges[i][3]);
continue;
// 是关键边就不可能是伪关键边，就不用往下判断了
}
// 在不是关键边的基础上判断其是否为伪关键边
// 方法是优先考虑这条边 先把这条边加入最小生成树中 然后执行一遍kruskal算法
// 如果最小生成树的权值仍然是initval
// 那么就说明它虽然不是关键边，
// 关键边根据其定义它肯定会出现在所有最小生成树中
// 这个边不是关键边，不会出现在所有最小生成树中，
// 但是它却可以出现在某一个最小生成树中
// 那么它就是伪关键边
u.restate();
curval = 0;
curcnt = 0;
int x = edges[i][0], y = edges[i][1], t = edges[i][2];
curval += t;
curcnt++;
u.p[x] = y;
for (int j = 0; j < m; ++j)
{
if (j != i)
{
int a = edges[j][0], b = edges[j][1], w = edges[j][2];
a = u.find(a), b = u.find(b);
if (a != b)
{
curval += w;
++curcnt;
u.p[a] = b;
}
}
}
if (curcnt == n - 1 && curval == initval)
{
ans[1].push_back(edges[i][3]);
}
}
return ans;
}
};
二、二分图
1 染色法判断二分图
I 算法思想
二分图的定义就是可以把所有点划分到两边去，使得所有边都是在集合之间的，集合内部没有边。
一个图是二分图当且仅当图中不含奇数环(环中的边的个数是奇数)，insight见下图。
必要性：
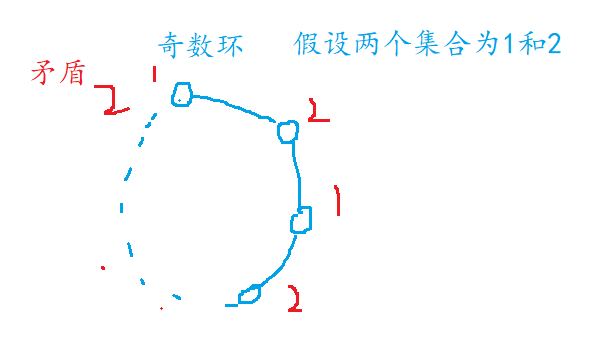
充分性：
采用一个构造的过程，我们先对任意一个尚未被染色的点染色为1或2，表示其在1集合或2集合，然后所有与它相邻的点就都可以染色，然后再找一个尚未被染色的点重复上述过程，因为图中不存在奇数环，所以这个染色的过程是没有矛盾的，所以这样就构造出了一个二分图，也就证明了不含奇数环的图一定是一个二分图。
所以我们证明了如果染色过程中没有出现矛盾，那么这个图就是一个二分图，否则这个图就不是二分图。
由于深搜代码更短，所以我们用深搜给点染色：
II 模板题
#include <iostream>
#include <cstring>
using namespace std;
const int N = 1e5 + 10;
const int M = 2e5 + 10;// 二分图都是无向图 因此边数是两倍
int n, m;
int h[N], e[M], ne[M], idx = 0;// 邻接表
int color[N]; // 表示每个点的染色情况
void init()
{
memset(h, -1, sizeof(h));
}
void add(int a, int b)
{
e[idx] = b;
ne[idx] = h[a], h[a] = idx++;
}
bool dfs(int u, int c)
{
color[u] = c;// 染色
// 染色其连通边并且看看有没有矛盾
for (int i = h[u]; i != -1; i = ne[i])
{
int j = e[i];
// 如果j未被染色
if (!color[j])
{
// 给j染另一个色 并且判断是否有染色矛盾发生
if (!dfs(j, 3 - c)) return false;
}
// 否则j被染色了 如果染色为同一色就矛盾了
else
{
if (color[j] == c) return false;
}
}
// 走到这里说明这个点开始dfs没有矛盾 返回true
return true;
}
int main()
{
init();
// 处理输入并建图
cin >> n >> m;
int a, b;
while (m--)
{
cin >> a >> b;
add(a, b), add(b, a);
}
// 对每个点 如果未被染色， 则进行dfs
bool flag = false;// 表示是否有矛盾出现
// 有矛盾则改为true
for (int i = 1; i <= n; ++i)
{
if (!color[i])
{
// dfs返回true表示没有染色矛盾发生
// 否则表示有染色矛盾发生
if (!dfs(i, 1))
{
flag = true;
break;
}
}
}
if (flag) puts("No");
else puts("Yes");
return 0;
}
III LeetCode 785.判断二分图
class Solution {
public:
vector<int> color;
bool dfs(int u, int c, const vector<vector<int>>& graph)
{
color[u] = c;
for (int j : graph[u])
{
if (!color[j])
{
if (!dfs(j, 3 - c, graph)) return false;
}
else
{
if (color[j] == c) return false;
}
}
return true;
}
bool isBipartite(vector<vector<int>>& graph)
{
int n = graph.size();
color = vector<int>(n, 0);
bool ret = true;
for (int i = 0; i < n; ++i)
{
if (!color[i])
{
if (!dfs(i, 1, graph))
{
ret = false;
break;
}
}
}
return ret;
}
};
IV LeetCode886. 可能的二分法
原题链接：886. 可能的二分法
把两个人之间的不喜欢看做是图中两个结点的一个无相边，那么本题就是一个典型的判断二分图问题。
class Solution {
public:
static const int N = 2e3 + 10;
static const int M = 2e4 + 10;
int h[N], ne[M], e[M], idx = 0;
int color[N] = {0};
int _n;
void init()
{
memset(h, -1, sizeof(h));
}
void add(int a, int b)
{
e[idx] = b;
ne[idx] = h[a], h[a] = idx++;
}
bool dfs(int u, int c)
{
color[u] = c;
for (int i = h[u]; i != -1; i = ne[i])
{
int j = e[i];
if (!color[j])
{
if (!dfs(j, 3 - c)) return false;
}
else
{
if (color[j] == c) return false;
}
}
return true;
}
bool possibleBipartition(int n, vector<vector<int>>& dislikes)
{
_n = n;
init();
for (auto& dis : dislikes)
{
int a = dis[0], b = dis[1];
add(a, b), add(b, a);
}
bool flag = true;
for (int i = 1; i <= n; ++i)
{
if (!color[i])
{
if (!dfs(i, 1))
{
flag = false;
break;
}
}
}
return flag;
}
};
2 二分图的最大匹配—匈牙利算法
I 算法思想
一个成功的匹配指的是没有两条边是公用一个点的，匈牙利算法可以返回成功匹配中匹配对数最大是多少。
时间复杂度：所有点n,最坏遍历所有边m,时间复杂度O(nm)。
II 模板题
#include <iostream>
#include <cstring>
using namespace std;
const int N = 510;
const int M = 1e5 + 10;
int h[N], e[M], ne[M], idx = 0;
int match[N];// 表示当前妹子匹配的哪一号男生
bool st[N];// 表示在对某个男生的此轮考虑中 这个妹子是否被匹配过了
int n1, n2, m;
void init()
{
memset(h, -1, sizeof(h));
}
void add(int a, int b)
{
e[idx] = b;
ne[idx] = h[a], h[a] = idx++;
}
bool find(int x)
{
// 考虑所有与该男生相连的点
for (int i = h[x]; i != -1; i = ne[i])
{
int j = e[i];
// 如果在此轮匹配中未被考虑过
if (!st[j])
{
st[j] = true;// 该点被考虑过了
// 如果这个妹子还没有相连的点或者她相连的点可以换一个点去连
// 那么x就可以与j匹配
if (match[j] == 0 || find(match[j]) == true)
{
match[j] = x;
return true;
}
}
}
return false;
}
int main()
{
init();
cin >> n1 >> n2 >> m;
int a, b;
while (m--)
{
cin >> a >> b;
add(a, b);// 只用考虑男生的那边 所以直接只加单向边即可
}
int res = 0;
// 考虑每一个男生
for (int i = 1; i <= n1; ++i)
{
// 先把所有妹子的考虑情况都清空
memset(st, false, sizeof(st));
if (find(i)) res++;
}
printf("%d\n", res);
return 0;
}
III Acwing372.棋盘覆盖
原题链接：Acwing372.棋盘覆盖
补充概念：
增广路径：从非匹配点开始，经过一条非匹配边，一条匹配边，走到另一个非匹配点的一条路径。
二分图的一个匹配是最大匹配当且仅当不存在增广路径。
本题难就难在看出它是一个二分图问题。
把一个矩阵中的相邻的两个位置看做是图的两个点，如果这两个点能够放一块牌，则在它们两个点之间连一条边，那么本问题就转化为了最多能从图里头取出多少条边的问题，因为卡片不重叠，所以所有选出来的边都不能有公共点，这就转化为了找图中的最大匹配的问题。
但是本题还未完全转化为一个二分图问题，我们还要判断一下我们建的图是否为二分图，判断图是否为二分图就是看看这个图能否进行二染色，使得边上两个点都是不同颜色的。
这是可以的，我们可以把格子都分成两种：奇数格和偶数格，
发现一个n * n的矩阵的点一定可以被二染色，由此所有的边必然是一个白格一个绿格，所以我们的图一定是个二分图。
判断当前点是奇数格子还是偶数格子，对当前点的下标求和判断就行即可。
本题看起来和二分图毫无关系，居然可以用二分图做，实在是巧妙。
#include <iostream>
#include <cstring>
#include <utility>
using namespace std;
typedef pair<int, int> PII;// 因为妹子匹配的点也是个矩阵中的点 二元组
const int N = 110;
bool g[N][N];// g[i][j] = true表示这个点是坏点
PII match[N][N]; // 妹子i,j匹配的对象
bool st[N][N]; // 防止重复遍历
int n, t;
int dx[4] = { 1, -1, 0, 0 };
int dy[4] = { 0, 0, -1, 1 };
bool find(int x, int y)
{
// 所有与x相邻的点:上下左右 也就是能与它匹配的点
for (int i = 0; i < 4; ++i)
{
int nx = x + dx[i];
int ny = y + dy[i];
// 出界
if (nx < 1 || nx > n || ny < 1 || ny > n) continue;
// 看看是否考虑过 且它不是坏点
if (!st[nx][ny] && !g[nx][ny])
{
st[nx][ny] = true;
if (match[nx][ny].first == 0 || find(match[nx][ny].first, match[nx][ny].second))
{
match[nx][ny] = { x, y };
return true;
}
}
}
return false;
}
int main()
{
// 处理输入输出
cin >> n >> t;
int a, b;
// 标记坏格子
while (t--)
{
cin >> a >> b;
g[a][b] = true;
}
// 匈牙利算法
int cnt = 0;
for (int i = 1; i <= n; ++i)
{
for (int j = 1; j <= n; ++j)
{
// 这里遍历偶数格子为例
if (!g[i][j] && (i + j) % 2 == 0)
{
memset(st, false, sizeof(st));
if (find(i, j)) ++cnt;
}
}
}
printf("%d\n", cnt);
return 0;
}
下面再给一道LCP的类似题目来巩固一下。
IV LCP 04. 覆盖
原题链接：LCP 04. 覆盖
分析：
首先我们把矩阵中的每个点都看做是一个图中的点，如果相邻的两个点之间可以摆放骨牌则说明这两个点之间有一条边，问题就转化为了最多能从图中取出多少条边的问题。
又考虑到骨牌之间不能重叠，我们摆放骨牌的最大数目就可以转化为图的最大匹配问题，下面我们再把本题转化为一个二分图的最大匹配问题，具体方法就是把矩阵中的点进行奇偶染色：
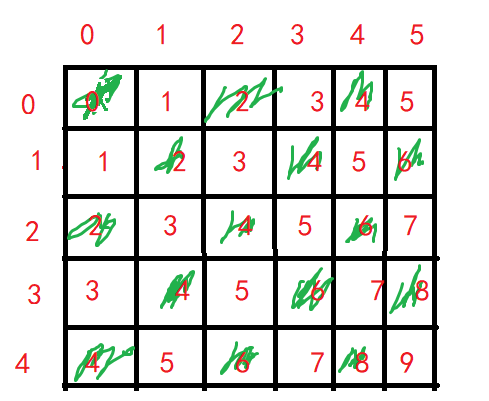
这样与一个点相邻的四个点都是另一个集合的点，本图确实是一个二分图。
至此，本题转化为了一个二分图的最大匹配问题，可以使用匈牙利算法解决。
class Solution {
public:
typedef pair<int, int> PII;
static const int N = 10;
bool g[N][N];
PII match[N][N];
bool st[N][N];
int dx[4] = {1, -1, 0, 0};
int dy[4] = {0, 0, -1, 1};
int _n, _m;
bool find(int x, int y)
{
// 找与它相连的点 即它的上下左右四个点
for (int i = 0; i < 4; ++i)
{
int nx = x + dx[i], ny = y + dy[i];
if (nx < 0 || nx >= _n || ny < 0 || ny >= _m) continue;
if (!g[nx][ny] && !st[nx][ny])
{
st[nx][ny] = true;
PII p = match[nx][ny];
if (p.first == -1 || find(p.first, p.second))
{
match[nx][ny] = {x, y};
return true;
}
}
}
return false;
}
int domino(int n, int m, vector<vector<int>>& broken)
{
_n = n;
_m = m;
memset(g, false, sizeof(g));
for (int i = 0; i < n; ++i)
for (int j = 0; j < m; ++j)
match[i][j] = {-1, -1};
// 把不能放的点读入g数组
for (auto& brk : broken)
{
int a = brk[0], b = brk[1];
g[a][b] = true;
}
// 匈牙利算法
int res = 0;
for (int i = 0; i < n; ++i)
{
for (int j = 0; j < m; ++j)
{
// 遍历下标和为偶数的点 注意 不能是不能匹配的点
if (!g[i][j] && (i + j) % 2 == 0)
{
memset(st, false, sizeof(st));
if (find(i, j)) ++res;
}
}
}
return res;
}
};
扫一扫
1428
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
