算法学习笔记：22.贪心算法之霍夫曼编码 ——从原理到实战，涵盖 LeetCode 与考研 408 例题

霍夫曼编码（Huffman Coding）是贪心算法在数据压缩领域的经典应用，由大卫・霍夫曼于 1952 年提出。它通过构建最优前缀编码树，实现对字符的高效压缩，在文件压缩（如 ZIP、GZIP）、通信编码等领域有着广泛应用。

霍夫曼编码核心思路

算法背景与目标

在数据传输中，若每个字符用等长二进制编码（如 ASCII 码），会存在冗余。霍夫曼编码的目标是：为出现频率高的字符分配短编码，频率低的字符分配长编码，且保证编码为前缀编码（任一字符的编码不是其他字符编码的前缀），从而实现无歧义解码并最小化总编码长度。

贪心策略与霍夫曼树

霍夫曼编码的核心是构建霍夫曼树（最优二叉树），其构建过程遵循贪心策略：每次选择两个频率最低的节点合并为一个新节点，新节点的频率为两节点频率之和，重复此过程直至只剩一个节点。

霍夫曼树的特点：

• 字符作为叶子节点，非叶子节点为合并生成的中间节点。

• 编码规则：左分支为 0，右分支为 1，从根到叶子的路径即为该字符的编码。

• 总编码长度（带权路径长度）最小，满足总长度 = Σ(字符频率 × 编码长度)。

算法步骤

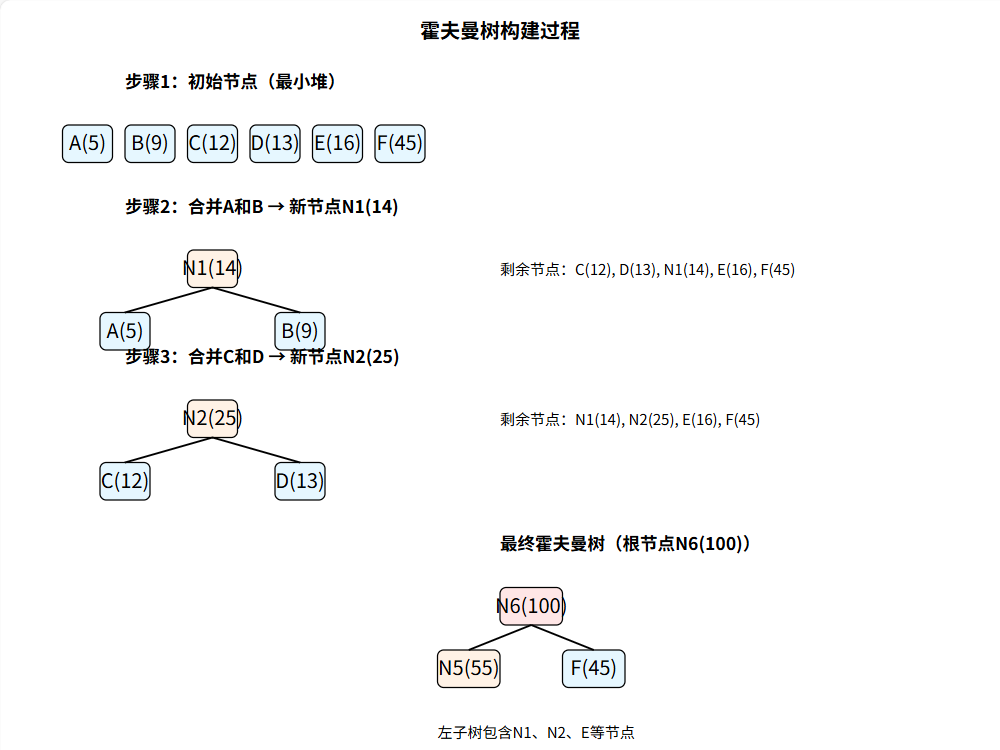
1. 初始化：为每个字符创建叶子节点，频率为该字符的出现次数。
2. 构建霍夫曼树：

• • 将所有叶子节点放入最小优先队列（最小堆）。
• • 重复以下步骤直至队列只剩一个节点：

• • • 取出两个频率最小的节点a和b。

• • • 创建新节点c，频率为a.freq + b.freq，a和b分别作为c的左右子树。

• • • 将c放入队列。

1. 生成编码：从根节点出发，遍历霍夫曼树，左分支记 0，右分支记 1，记录每个叶子节点（字符）的编码。

构建过程

（以字符频率 A:5, B:9, C:12, D:13, E:16, F:45 为例）

LeetCode 例题实战

例题 1：1167. 连接棒材的最低费用（中等）

题目描述：有一些长度不同的棒材，每连接两根长度为x和y的棒材，费用为x + y。连接所有棒材的总费用最低是多少？

示例：

输入：[1,8,3,5]

输出：30

解释：

1. 连接1和3 → 费用4，棒材变为[4,5,8]

2. 连接4和5 → 费用9，棒材变为[9,8]

3. 连接9和8 → 费用17，总费用4+9+17=30

解题思路

本题与霍夫曼树构建思路完全一致：每次选择最短的两根棒材连接，总费用最低（贪心策略）。通过最小优先队列（最小堆）实现每次取最小的两个元素。

算法步骤

1. 将所有棒材长度放入最小堆。
2. 若堆中元素数≥2，取出两个最小元素a和b，计算费用a + b，将其加入总费用，并将a + b放入堆中。
3. 重复步骤 2 直至堆中只剩一个元素，返回总费用。

代码实现

import java.util.PriorityQueue;

class Solution {

    public int connectSticks(int[] sticks) {

        if (sticks == null || sticks.length <= 1) {

            return 0;

        }

// 初始化最小堆

        PriorityQueue<Integer> minHeap = new PriorityQueue<>();

        for (int s : sticks) {

            minHeap.add(s);

        }

        int totalCost = 0;

        while (minHeap.size() > 1) {

// 取出两个最小元素

            int a = minHeap.poll();

            int b = minHeap.poll();

            int cost = a + b;

            totalCost += cost;

// 合并后放回堆

            minHeap.add(cost);

        }

        return totalCost;

    }

}

复杂度分析

• 时间复杂度：O (nlogn)，堆的插入和删除操作均为 O (logn)，共执行 O (n) 次。

• 空间复杂度：O (n)，堆存储所有元素。

例题 2：621. 任务调度器（中等）

题目描述：给定字符数组tasks（任务列表），冷却时间n（相同任务之间至少间隔n个单位时间）。完成所有任务的最短时间是多少？

示例：

输入：tasks = ["A","A","A","B","B","B"], n = 2

输出：8

解释：A→B→(待命)→A→B→(待命)→A→B（总时间8）

解题思路

本题可借助霍夫曼编码的贪心思想：优先安排出现频率最高的任务，减少空闲时间。

1. 计算每个任务的频率，放入最大堆（优先处理高频任务）。
2. 每次从堆中取前n+1个不同任务执行（或用待命填充），记录时间，更新频率后将剩余任务放回堆。
3. 重复直至所有任务完成。

代码实现

import java.util.*;

class Solution {

    public int leastInterval(char[] tasks, int n) {

// 计算任务频率

        int[] freq = new int[26];

        for (char c : tasks) {

            freq[c - 'A']++;

        }

// 最大堆（按频率降序）

        PriorityQueue<Integer> maxHeap = new PriorityQueue<>((a, b) -> b - a);

        for (int f : freq) {

            if (f > 0) {

                maxHeap.add(f);

            }

        }

        int time = 0;

        while (!maxHeap.isEmpty()) {

            List<Integer> temp = new ArrayList<>();

            int cycle = n + 1; // 一个周期最多处理n+1个任务

// 处理一个周期的任务

            while (cycle > 0 && !maxHeap.isEmpty()) {

                int curr = maxHeap.poll() - 1; // 执行一次任务

                if (curr > 0) {

                    temp.add(curr); // 剩余次数待处理

                }

                time++;

                cycle--;

            }

// 放回剩余任务

            maxHeap.addAll(temp);

// 若堆不为空，需补全待命时间

            if (!maxHeap.isEmpty()) {

                time += cycle;

            }

        }

        return time;

    }

}

复杂度分析

• 时间复杂度：O(m log 26) ≈ O(m)，m为任务总数，堆中最多 26 个元素（字母）。

• 空间复杂度：O (26) = O (1)，存储频率和堆。

考研 408 例题解析

例题 1：霍夫曼编码构造与编码长度计算（高频考点）

题目：给定字符集{a, b, c, d, e}及其频率{4, 2, 5, 3, 1}，构建霍夫曼树并计算：

1. 每个字符的霍夫曼编码。

1. 总编码长度（带权路径长度）。

解题步骤（手动构建霍夫曼树）

1. 初始节点：频率1(e), 2(b), 3(d), 4(a), 5(c)。
2. 第一次合并：e (1) 和 b (2) → 新节点 N1 (3)。
3. 第二次合并：N1 (3) 和 d (3) → 新节点 N2 (6)。
4. 第三次合并：a (4) 和 N2 (6) → 新节点 N3 (10)。
5. 第四次合并：c (5) 和 N3 (10) → 根节点 N4 (15)。

霍夫曼编码（左 0 右 1）

• e：000（路径：N4→N3→N2→N1→e）

• b：001（路径：N4→N3→N2→N1→b）

• d：01（路径：N4→N3→N2→d）

• a：10（路径：N4→N3→a）

• c：11（路径：N4→c）

总编码长度

1×3 + 2×3 + 3×2 + 4×2 + 5×2 = 3 + 6 + 6 + 8 + 10 = 33。

答案总结

1. 编码：e:000, b:001, d:01, a:10, c:11。
2. 总编码长度：33。

例题 2：霍夫曼算法正确性证明（考研理论题）

题目：证明霍夫曼编码的总编码长度是最优的（即不存在更短的前缀编码）。

解题思路（贪心选择性质 + 最优子结构）

1. 贪心选择性质：设频率最低的两个字符为x和y，则存在最优编码使x和y的编码长度相同，且仅最后一位不同（即它们在霍夫曼树中为兄弟节点）。

• • 反证法：假设最优编码中x和y不是兄弟，替换为兄弟节点后总长度不增加，与 “最优” 矛盾。

1. 最优子结构：若T是字符集C的最优霍夫曼树，将x和y合并为z（频率x.freq + y.freq），则T'（含z的树）是字符集C' = (C - {x,y}) ∪ {z}的最优树。

• • 反证法：若T'不是最优，则存在更优树T''，替换后T的总长度更优，矛盾。

结论

霍夫曼算法通过贪心选择和最优子结构，构建的编码树总长度最优。

霍夫曼编码的扩展与应用

实际应用场景

• 数据压缩：ZIP、GZIP、JPEG 等压缩算法中，霍夫曼编码用于减少冗余数据。

• 通信编码：卫星通信、网络传输中，用霍夫曼编码提高带宽利用率。

• 频率相关问题：如任务调度、资源分配等，需优先处理高频项的场景。

与其他编码的对比

编码方式	特点	适用场景
霍夫曼编码	变长编码，前缀编码	字符频率差异大的场景
香农 - 范诺编码	变长编码，前缀编码	理论最优，实现较复杂
定长编码	等长编码（如 ASCII）	字符频率均匀或需快速解码

考研 408 备考要点

• 核心考点：霍夫曼树的构建步骤、编码生成、带权路径长度计算。

• 易错点：

1. 合并节点时必须选择两个最小频率的节点。
2. 编码长度计算需区分 “路径长度”（边数）和 “编码位数”（等于路径长度）。
3. 证明题需掌握贪心选择性质和最优子结构的逻辑。

总结

霍夫曼编码作为贪心算法的经典应用，其核心思想是 “优先处理频率最低的元素”，通过构建最优二叉树实现最小总编码长度。

掌握霍夫曼编码不仅需要理解算法步骤，更要领悟其背后的贪心思想 ——局部最优选择可导致全局最优解。在考研备考中，需重点练习手动构建霍夫曼树、计算编码长度，并理解其最优性证明的逻辑。

希望本文能够帮助读者更深入地理解贪心算法中霍夫曼编码算法，并在实际项目中发挥其优势。谢谢阅读！

---

希望这份博客能够帮助到你。如果有其他需要修改或添加的地方，请随时告诉我。