LLM学习之路-01-第一章-预训练/最美的数学公式-欧拉公式

1. 导入

也许你在某些场合听说过欧拉公式，也许你干脆对数学不感冒。机缘巧合下，你点开了这篇文章，大致浏览了下然后关闭，继续为自己的工作学习忙碌。这不妨碍你暂停忙碌的脚步，欣赏她的美。 若干年后，你应该不曾记得看过这篇文章，但你会记得数学界有一个很美的公式。

2. 欧拉公式

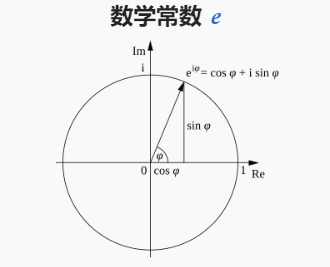
欧拉公式（Euler's formula）是复分析领域的公式，它将三角函数与复指数函数关联起来，因其提出者莱昂哈德·欧拉而得名。欧拉公式提出，对任意实数 x，都存在： $$ e^{ix} = \cos(x) + i\sin(x) $$ 其中 e是自然对数的底数，i是虚数单位，而 cos和 sin则是余弦、正弦对应的三角函数，参数 x则以弧度为单位。

这是一个非常美丽的公式，它将三角函数，指数函数，复数联系在了一起，是数学中的一颗明珠。

3.欧拉恒等式是欧拉恒等式（Euler's identity）是欧拉公式的一个特例，当 x = π 时，欧拉公式变为： $$ e^{i\pi} + 1 = 0 $$ 这个公式被认为是数学中最美丽的公式之一，它将五个最重要的数学常数联系在了一起：0、1、e、i和π。

4. 欧拉的贡献

莱昂哈德·欧拉（1707年4月15日—1783年9月18日），瑞士数学家、物理学家、天文学家、地理学家、逻辑学家和工程师。近代数学先驱之一。

欧拉在包括微积分和图论在内的多个数学领域都做出过重大贡献。他引进和推广了许多数学术语和书写格式，并一直沿用至今，例如：

• 函数的记法f(x)  ；
• 虚数单位 √-1的记法i；
• 圆周率的记法π  ；
• 求和符号 Σ ；
• 差分符号 Δ ;
• 用小写字母表示三角形的边和用大写字母表示三角形的角等；
• 给出了自然对数的底数$e$定义，其也称为欧拉数(Euler's number)；
• 此外，他还在力学、流体动力学、光学、天文学和乐理领域有突出的贡献。

欧拉是18世纪杰出的数学家，同时也是有史以来最伟大的数学家之一。他也是一位多产作者，其学术著作有60-80册。

欧拉逝世后，几位著名的数学家高度评价他对数学的贡献，例如法国数学家皮埃尔-西蒙·拉普拉斯曾这样评价欧拉对于数学的贡献：“读欧拉的著作吧，在任何意义上，他都是我们的大师”。

德国数学家卡尔·弗里德里希·高斯曾写道：“对欧拉所有的著作的研究将永远是数学各个领域最好的学习之所，没有任何其他东西可以取代它”。