LeetCode 33. 搜索旋转排序数组

注：该篇文章已与我的个人博客同步更新。欢迎移步https://cqh-i.github.io/体验更好的阅读效果。

题目描述

假设按照升序排序的数组在预先未知的某个点上进行了旋转。
(例如，数组[0,1,2,4,5,6,7]可能变为[4,5,6,7,0,1,2])。
搜索一个给定的目标值，如果数组中存在这个目标值，则返回它的索引，否则返回-1。
你可以假设数组中不存在重复的元素。
你的算法时间复杂度必须是O(logn)级别。
示例 1:

输入: nums = [4,5,6,7,0,1,2], target = 0
输出: 4

示例 2:

输入: nums = [4,5,6,7,0,1,2], target = 3
输出: -1

思路:

题目要求时间复杂度为O(logn), 很容易想到使用二分查找算法, 但它给的升序数组是进行旋转的, 且数组中不存在重复的元素, 我们要判断给定数组的中间元素mid与旋转点的关系, 共有两种情况:

• 如果mid的值比旋转点小(mid在旋转点下方), 那么[mid,high]之间的区间为严格的升序数组,[left,mid]被分成了两段(先增后减).以[6,7,1,0,2,4,5]为例, 如下图:
  
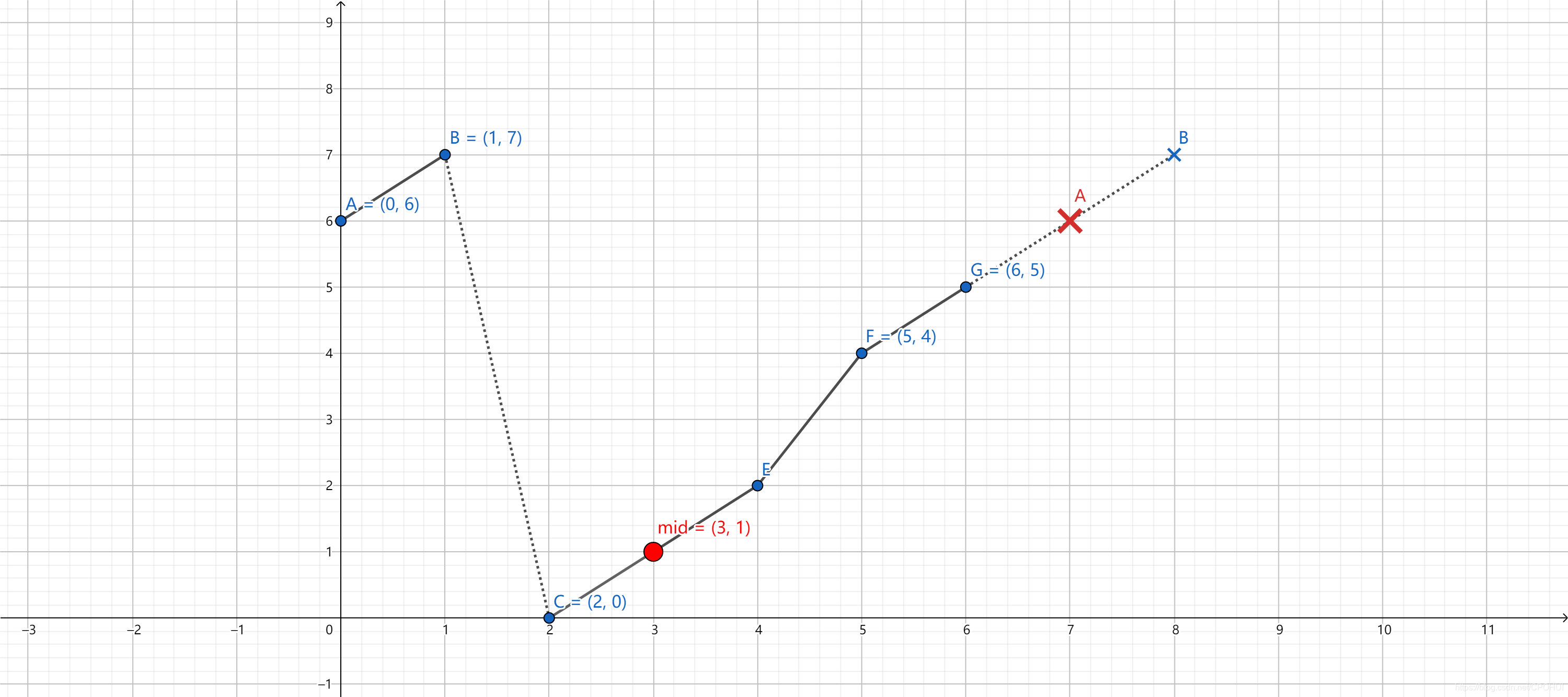
  此时如果nums[mid] < target <= nums[right], 则继续二分查找区间[mid+1, high]; 否则查找区间[low, mid - 1]
• 如果mid的值比旋转点大(mid在旋转点上方), 那么[low,mid]之间的区间为严格的升序数组,[mid,high]被分成了两段(先减后增).以[4,5,6,7,0,1,2]为例, 如下图:
  
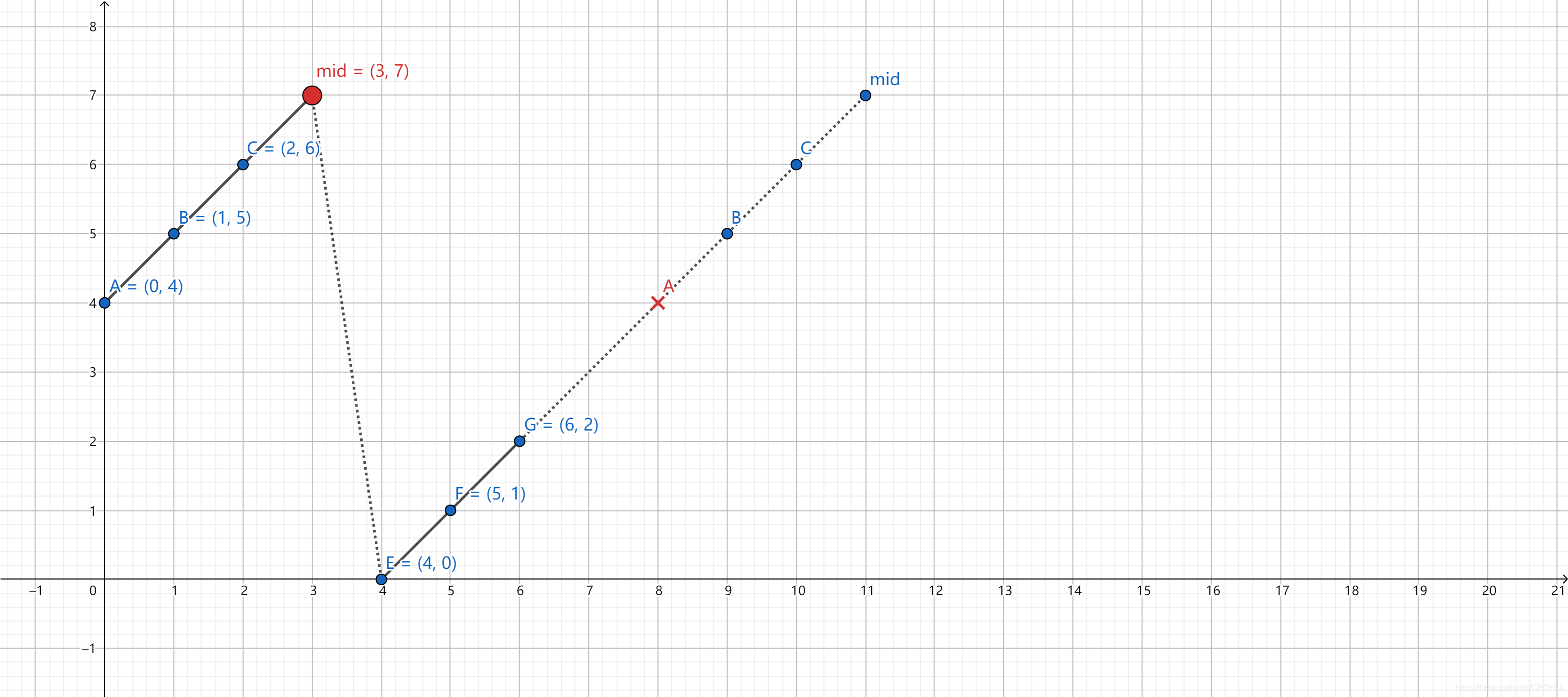
  此时如果nums[low] <= target < nums[mid], 则继续二分查找区间[low, mid - 1]; 否则查找区间[mid+1,high]

class Solution {
    public int search(int[] nums, int target) {
        if(nums == null || nums.length == 0) return -1;
        int length = nums.length;
        int high = length - 1;
        int low = 0;
        while(low <= high){
            int mid = low + (high - low) / 2;
            if(target == nums[mid]) 
                return mid;
            if(nums[mid] < nums[low]){
                if(target > nums[mid] && target <= nums[high]){
                    low = mid + 1;
                }else {
                    high = mid - 1;
                }
            }else{
                if(target >= nums[low] && target < nums[mid]){
                    high = mid - 1;
                }else {
                    low = mid + 1;
                }
            }
        }
        return -1;
    }
}