Batch Normalization(BN): Accelerating Deep Network Training by Reducing Internal Covariate Shift
批归一化:通过减少内部协方差偏移加快深度网络训练
本文提出Batch Normalization(BN)机制;
发表时间:[Submitted on 11 Feb 2015 (v1), last revised 2 Mar 2015 (this version, v3)];
发表期刊/会议:Computer Science > Machine Learning;
论文地址:https://arxiv.org/abs/1502.03167;
Inception发展演变:
- GoogLeNet/Inception V1)2014年9月 《Going deeper with convolutions》;
- BN-Inception 2015年2月 《Batch Normalization: Accelerating Deep Network Training by Reducing Internal Covariate Shift》;
- Inception V2/V3 2015年12月《Rethinking the Inception Architecture for Computer Vision》;
- Inception V4、Inception-ResNet 2016年2月 《Inception-v4, Inception-ResNet and the Impact of Residual Connections on Learning》;
- Xception 2016年10月 《Xception: Deep Learning with Depthwise Separable Convolutions》;
0 摘要
【问题挑战】训练深度神经网络很复杂,因为在训练过程中,随着前一层的参数变化,每一层输入的分布都会发生变化;
通过较低的学习率(lr)和仔细的参数初始化来解决,但会减慢训练速度,并且经常出现非线性饱和,最终导致深度网络难以训练(如sigmoid造成梯度消失问题);
【解决方法】将这种现象称为内部协方差偏移(internal covariate shift),并通过对网络层的输入进行归一化(BN)来解决这个问题。
【方法细节】本文的方法将标准化/归一化作为模型体系结构的一部分,并为每个训练小批量(mini-batch)执行标准化,从而发挥了其优势。
BN允许模型使用更高的学习率,并且不用小心翼翼的初始化,在某些情况下,还消除了对Dropout的需要。
将BN应用于分类模型,打败了原始模型,提高了性能;
1 简介
随机梯度下降(SGD)已被证明是一种训练深度网络的有效方法;
使用SGD,训练分step进行,每一step包含一个mini-batch;
使用mini-batch的优势:
- 每次使用一个batch可以大大减小收敛所需要的迭代次数,同时可以使收敛到的结果更加接近梯度下降的效果;
- 可实现并行化;
虽然SGD简单有效,但它需要仔细调整模型超参数,特别是学习率和初始参数值,训练起来非常复杂,因为每一层的输入都受到前面所有层的参数的影响,层的分布会变化;
在训练过程中,将深度网络内部节点分布的变化称为内部协方差偏移(前面层小的改变会造成后面层非常大的改变,蝴蝶效应)。
消除内部协方差偏移可以使模型训练更快。
本文提出了一种新机制,称之为批处理归一化(BN),它朝着减少内部协方差偏移迈出了一步,并通过这样做极大地加速了深度神经网络的训练。
使用标准化/归一化来修改每一层的均值和方差。减少梯度对参数或其初值尺度的依赖,对网络中的梯度流也有一个有益的影响,这样训练时就可以使用更大的学习率了(不会产生震荡)。
BN也有正则化的作用,减少dropout的使用。
2 相关工作
【LeCun et al., 1998b; Wiesler & Ney, 2011】
通过对每一层进行白化,使得网络训练更快;
【Wiesler et al., 2014; Raiko et al., 2012; Povey et al., 2014; Desjardins & Kavukcuoglu】
在每个训练步骤或某个间隔考虑白化激活,要么直接修改网络,要么通过改变优化算法的参数来依赖于网络激活值;
【Lyu & Simoncelli, 2008】
使用在单个训练示例上计算的统计数据,或者在图像网络的情况下,在给定位置的不同特征地图上计算统计数据;
3 方法:通过mini-batch实现BN

pytorch实现BN:
class BatchNorm(nn.module):
def __init__(self,num_features,num_dims):
super().__init__()
if num_dim == 2:
shape = (1,num_features)
else:
shape = (1,num_features,1,1)
# 参数初始化
self.gamma = nn.Parameter(torch.ones(shape))
self.beta = nn.Parameter(torch.ones(shape))
self.moving_mean = torch.zeros(shape)
self.moving_var = torch.zeros(shape)
def forward(self,X):
if self.moving_mean.device != X.device:
self.moving_mean = self.moving_mean.to(X.device)
self.moving_var = self.moving_var.to(X.device)
Y, self.gamma, self.beta, self.moving_mean, self.moving_var = batch_norm(X,self.gamma,self.beta,self.moving_mean,self.moving_var,eps=1e-5,momentum=0.9)
return Y
pytorch BN模块调用:
self.bn = nn.BatchNorm1d(num_features=3)
BN模块pytorch源码:
class _NormBase(Module):
"""Common base of _InstanceNorm and _BatchNorm"""
# 读checkpoint时会用version来区分是 PyTorch 0.4.1 之前还是之后的版本
_version = 2
__constants__ = ['track_running_stats', 'momentum', 'eps',
'num_features', 'affine']
def __init__(self, num_features, eps=1e-5, momentum=0.1, affine=True,
track_running_stats=True):
super(_NormBase, self).__init__()
self.num_features = num_features
self.eps = eps
self.momentum = momentum
self.affine = affine
self.track_running_stats = track_running_stats
if self.affine:
# 如果打开 affine,就使用缩放因子和平移因子
self.weight = Parameter(torch.Tensor(num_features))
self.bias = Parameter(torch.Tensor(num_features))
else:
self.register_parameter('weight', None)
self.register_parameter('bias', None)
# 训练时是否需要统计 mean 和 variance
if self.track_running_stats:
# buffer 不会在self.parameters()中出现
self.register_buffer('running_mean', torch.zeros(num_features))
self.register_buffer('running_var', torch.ones(num_features))
self.register_buffer('num_batches_tracked', torch.tensor(0, dtype=torch.long))
else:
self.register_parameter('running_mean', None)
self.register_parameter('running_var', None)
self.register_parameter('num_batches_tracked', None)
self.reset_parameters()
def reset_running_stats(self):
if self.track_running_stats:
self.running_mean.zero_()
self.running_var.fill_(1)
self.num_batches_tracked.zero_()
def reset_parameters(self):
self.reset_running_stats()
if self.affine:
init.ones_(self.weight)
init.zeros_(self.bias)
def _check_input_dim(self, input):
# 具体在 BN1d, BN2d, BN3d 中实现,验证输入合法性
raise NotImplementedError
def extra_repr(self):
return '{num_features}, eps={eps}, momentum={momentum}, affine={affine}, ' \
'track_running_stats={track_running_stats}'.format(**self.__dict__)
def _load_from_state_dict(self, state_dict, prefix, local_metadata, strict,
missing_keys, unexpected_keys, error_msgs):
version = local_metadata.get('version', None)
if (version is None or version < 2) and self.track_running_stats:
# at version 2: added num_batches_tracked buffer
# this should have a default value of 0
num_batches_tracked_key = prefix + 'num_batches_tracked'
if num_batches_tracked_key not in state_dict:
# 旧版本的checkpoint没有这个key,设置为0
state_dict[num_batches_tracked_key] = torch.tensor(0, dtype=torch.long)
super(_NormBase, self)._load_from_state_dict(
state_dict, prefix, local_metadata, strict,
missing_keys, unexpected_keys, error_msgs)
class _BatchNorm(_NormBase):
def __init__(self, num_features, eps=1e-5, momentum=0.1, affine=True,
track_running_stats=True):
super(_BatchNorm, self).__init__(
num_features, eps, momentum, affine, track_running_stats)
def forward(self, input):
self._check_input_dim(input)
# exponential_average_factor is set to self.momentum
# (when it is available) only so that it gets updated
# in ONNX graph when this node is exported to ONNX.
if self.momentum is None:
exponential_average_factor = 0.0
else:
exponential_average_factor = self.momentum
# 如果在train状态且self.track_running_stats被设置为True,就需要更新统计量
if self.training and self.track_running_stats:
if self.num_batches_tracked is not None:
self.num_batches_tracked = self.num_batches_tracked + 1
# 如果momentum被设置为None,就用num_batches_tracked来加权
if self.momentum is None:
exponential_average_factor = 1.0 / float(self.num_batches_tracked)
else: # use exponential moving average
exponential_average_factor = self.momentum
return F.batch_norm(
input, self.running_mean, self.running_var, self.weight, self.bias,
self.training or not self.track_running_stats,
exponential_average_factor, self.eps)
3.1 BN网络的训练与推理
训练阶段(mini-batch),每一层都进行BN处理(标准化+线性变换);
推理阶段(可能只传入一张图像进行推理),怎么计算均值和方差?——用训练集的均值和方差;
比如有100个mini-batch,从训练集(每层)得到100个均值/方差,推理时则对这100个均值/方差取均值;

3.2 BN卷积网络
BN网络可以应用任何激活函数(sigmoid\ReLu等),可以保证网络有效训练;
见实验部分;
3.3 BN网络可以用更大的学习率
见实验部分;
4 实验
4.1 随时间的激活
为了验证内部协方差偏移对训练的影响,以及BN对抗它的能力,我们考虑了在MNIST数据集上预测数字分类的问题;
实验结果如图1所示;
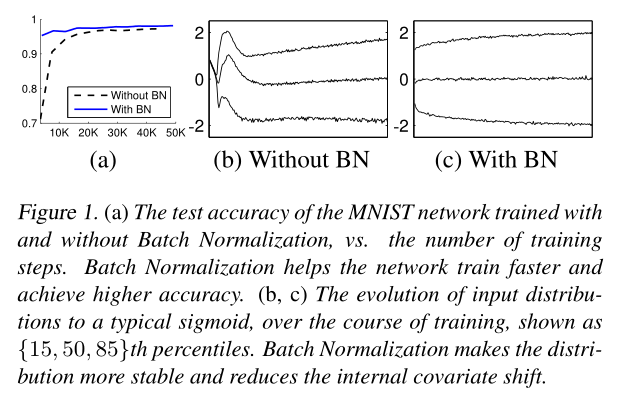
(a)MNIST数据集上,有BN与无BN的精度对比(横轴:epoch;纵轴:acc);
有BN操作在非常小的epoch就有非常高的精度(收敛快,训练快),有BN操作的精度整体比无BN操作的精度高;
(b)( c):展示了对于每个网络的最后一个隐藏层的一个典型激活sigmoid,其分布是如何演变的。原始网络中的分布随着时间的推移而显著变化,无论是均值还是方差,这使得后续层的训练变得复杂。相比之下,批量归一化网络中的分布随着训练的进行更加稳定,这有助于训练。
4.2 图像分类实验
4.2.1 BN加速网络训练
用BN的好处:
- 增大学习率(Increase learning rate):实现训练加速,并且没有副作用;
- 去除dropout(Remove Dropout):BN提供了与Dropout类似的正则化;
- 更好的打乱数据(Shuffle training examples more thoroughly):每张图像在不同mini-batch有不同的均值/方差,更好的打乱数据可以更好的训练网络;
- 减少 L 2 L_2 L2正则化的使用(Reduce the L2 weight regularization.):同dropout;
- 加速学习率的衰减(Accelerate the learning rate decay):学习率降低快,网络收敛快;
- 去除局部响应归一化(Remove Local Response Normalization):2014年VGG证明LRN没什么用;
- 减少光度失真(Reduce the photometric distortions):减少数据增强的使用;
4.2.2 单模型对比
Inception:原版GoogLeNet lr=0.0015;
BN-baseline:GoogLeNet+BN lr=0.0015;
BN-x5:在BN-baseline的基础上将学习率lr调整为0.0015 * 5 = 0.0075(对应3.3节);
BN-x30:在BN-baseline的基础上将学习率lr调整为0.0015 * 30 = 0.045(对应3.3节);
BN-x5-Sigmoid:在BN-x5的基础上,将ReLU替换为sigmoid(对应3.2节);

4.2.3 模型集成








 本文提出了BatchNormalization(BN)机制,用于解决深度神经网络训练中由于内部协方差偏移导致的复杂性问题。BN通过归一化每一层的输入,允许使用更高的学习率和更少的初始化敏感性,甚至在某些情况下可以替代Dropout。实验表明,BN能显著加速训练过程并提高模型性能。
本文提出了BatchNormalization(BN)机制,用于解决深度神经网络训练中由于内部协方差偏移导致的复杂性问题。BN通过归一化每一层的输入,允许使用更高的学习率和更少的初始化敏感性,甚至在某些情况下可以替代Dropout。实验表明,BN能显著加速训练过程并提高模型性能。
















 1000
1000

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








