【代码超详解】UVA 297 Quadtrees 四分树

一、题目描述

四分树是一种编码图像的算法。任意一个图像都可以被划分成四个象限，如果这四个象限仍然有像素的颜色不同，就把这个象限再划分成四个象限，直到象限只是单个点或者全部像素点的颜色都相同为止。
首先输入一个数字，代表测试用例的数量。在这若干个样例中，每个样例占一行，用于描述四分树。每一行的每个字符只能是 p、f、e 三个中的一个。p代表该节点为父节点，接下来输入其子节点。f 代表该节点要被涂成黑色，e 代表该节点留白。
现在有一个计算机艺术家正在创作一幅 32 × 32 像素的黑白图像。制图步骤如下：给两张 32 × 32 的黑白图，并将两个图像叠加。如果两张图对应的像素点有一个是黑色，那么合成后的图像对应的像素点也是黑色；否则合成结果的这个对应像素是白色。
对每一个测试用例，输出最终图像含有黑色像素的数目，格式是：
There are X black pixels.
X 代表统计出的最终图像含有的黑色像素的数量。
样例说明：
ppeeefpffeefe
pefepeefe

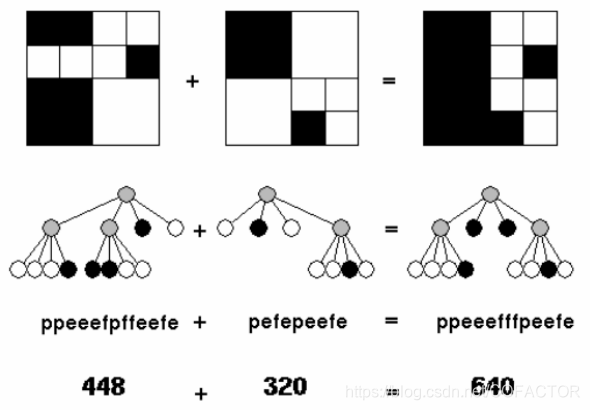
第一幅图：
第一个 p ：读取第一层子区域，范围为第一章图的右上角的四个小方块拼起来的一个大方块，长度为 16 。也就是说，区域是 (0，16) ，(0，31)，（16，16），（16，31）围成的正方形。
第二个 p ：读取第二层子区域，范围是 (0，24），（0，31），（8，24），（8，31）围成的正方形，边长为 8 。
eeef ：设上一步的区域为 D ，D 及其左侧、左下方、下方的三个等大的正方形区域的颜色分别为白、白、白、黑。第二层子区域的第一个节点的子节点绘制完毕。
p ：读取第一层子区域的第二个节点。
ffee ：该节点的四个象限的颜色分别为黑、黑、白、白。
fe ：读取第一层子节点的第三、第四个节点并绘制。
第二幅图：
p ：读取第一层子区域。
efe ：第一层子区域的第一、二、三节点的颜色分别为白、黑、白。
p：从第一层的第四子节点读取第二层的区域。
eefe ：该节点的四个子区域的颜色分别为白、白、黑、白。
第一个测试样例读取并绘制完毕。

二、算法分析说明与代码编写指导

准备一个字节数组 bitset<32> px[32] 用于储存合成后的结果。
采用递归输入的方式。编写一个渲染图像的函数，当读到字符 p 时调用四次该函数分别渲染四个象限。如果读到字符 f，并且该像素点是空白，就将其涂黑，黑色像素点的数量 n 要增加 1。如果读到字符 e，跳过。
写主程序时，需要注意一个测试案例要读取两个图像。读取第二张图的描述字符时，需要将当前字符位置 p 归位，而读取完该样例以后，才清空黑像素的数量 n ，并清除合成图像。

三、AC 代码（0 ms）

#include<cstdio>
#include<cstdlib>
#include<algorithm>
#include<bitset>
#pragma warning(disable:4996)
using namespace std;
const unsigned short pInit = 65535; unsigned int tc; bitset<32> px[32]; char descr[pInit]; unsigned short p, n;
inline void RenderImage(const char* descr, const unsigned short& pos, const unsigned char& row, const unsigned char& column, const unsigned char& len) {
	switch (descr[++p]) {
	case 'p':
		RenderImage(descr, p, row, column + len / 2, len / 2); RenderImage(descr, p, row, column, len / 2);
		RenderImage(descr, p, row + len / 2, column, len / 2); RenderImage(descr, p, row + len / 2, column + len / 2, len / 2); break;
	case 'f':
		unsigned char rowEnd = row + len, columnEnd = column + len;
		for (unsigned char i = row; i < rowEnd; ++i)
			for (unsigned char j = column; j < columnEnd; ++j)
				if (px[i][j] == 0) { px[i][j] = 1; ++n;  }
	}
}
int main() {
	scanf("%u", &tc); ++tc;
	while (--tc) {
		n = 0; p = pInit;
		for (unsigned char i = 0; i < 32; ++i)px[i].reset();
		scanf("%s", descr); RenderImage(descr, p, 0, 0, 32); p = pInit; scanf("%s", descr); RenderImage(descr, p, 0, 0, 32);
		printf("There are %hu black pixels.\n", n);
	}
	//system("pause");
	return 0;
}